Toptailieu.vn xin giới thiệu 06 câu trắc nghiệm Bài tập cuối chương 4 Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
06 câu trắc nghiệm Bài tập cuối chương 4 Kết nối tri thức (có đáp án 2023) CHỌN LỌC
Lý thuyết
1. Khái niệm vectơ
- Vectơ là một đoạn thẳng có hướng, nghĩa là, trong hai điểm mút của đoạn thẳng, đã chỉ rõ điểm đầu, điểm cuối.
- Độ dài vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
Chú ý:
+ Vectơ có điểm đầu A và điểm cuối B được kí hiệu là ![]() , đọc là vectơ AB.
, đọc là vectơ AB.
+ Để vẽ một vectơ, ta vẽ đoạn thẳng nối điểm đầu và điểm cuối của nó, rồi đánh dấu mũi tên ở điểm cuối.

+ Vectơ còn được kí hiệu là ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…
,…
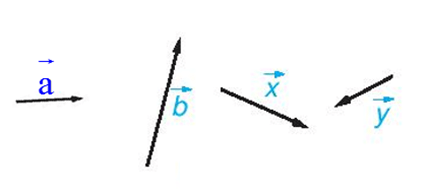
+ Độ dài của vectơ ![]() ,
, ![]() tương ứng được kí hiệu là |
tương ứng được kí hiệu là |![]() |, |
|, |![]() |.
|.
2. Hai vectơ cùng phương, cùng hướng, bằng nhau.
+ Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.
+ Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
+ Đối với hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.
+ Hai vectơ ![]() và
và ![]() được gọi là bằng nhau, kí hiệu là
được gọi là bằng nhau, kí hiệu là ![]() =
= ![]() , nếu chúng có cùng độ dài và cùng hướng.
, nếu chúng có cùng độ dài và cùng hướng.
Ví dụ:

Trong hình trên đường thẳng m đi qua điểm đầu và điểm cuối của vectơ ![]() , nên đường thẳng m gọi là giá của vectơ
, nên đường thẳng m gọi là giá của vectơ ![]() .
.
Tương tự, đường thẳng n là giá của hai vectơ ![]() và
và ![]() .
.
Đường thẳng m và n song song với nhau nên ba vectơ ![]() và
và ![]() và là các vectơ cùng phương.
và là các vectơ cùng phương.
![]() và
và ![]() cùng phương nhưng ngược hướng;
cùng phương nhưng ngược hướng; ![]() và
và ![]() cùng phương vàcùng hướng.
cùng phương vàcùng hướng.
Hai vectơ ![]() và
và ![]() cùng hướng, ngoài ra chúng có độ dài bằng nhau nên
cùng hướng, ngoài ra chúng có độ dài bằng nhau nên ![]() =
= ![]() .
.
Chú ý:
+ Ta cũng xét các vectơ điểm đầu và điểm cuối trùng nhau (chẳng hạn ![]() ,
, ![]() ), gọi là các vectơ–không.
), gọi là các vectơ–không.
+ Ta quy ước vectơ–không có độ dài bằng 0, cùng hướng (do đó cùng phương) với mọi vectơ.
+ Các vectơ–không có cùng độ dài và cùng hướng nên bằng nhau và được kí hiệu chung là ![]() .
.
+ Với mỗi điểm O và vectơ ![]() cho trước, có duy nhất điểm A sao cho
cho trước, có duy nhất điểm A sao cho ![]() =
= ![]() .
.
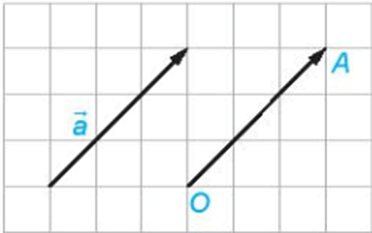
Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi ![]() và
và ![]() cùng phương.
cùng phương.

Chú ý: Ta có thể dùng vectơ để biểu diễn các đại lượng như lực, vận tốc, gia tốc. Hướng của vectơ chỉ hướng của đại lượng, độ dài của vectơ thể hiện cho độ lớn của đại lượng và được lấy tỉ lệ với độ lớn của đại lượng.
3. Tổng của hai vectơ
- Cho hai vectơ ![]() và
và ![]() . Lấy một điểm A tùy ý và vẽ
. Lấy một điểm A tùy ý và vẽ ![]() =
= ![]() ,
, ![]() =
= ![]() . Khi đó vectơ
. Khi đó vectơ ![]() được gọi là tổng của hai vectơ
được gọi là tổng của hai vectơ ![]() và
và ![]() và được kí hiệu là
và được kí hiệu là ![]() +
+ ![]() .
.
– Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.
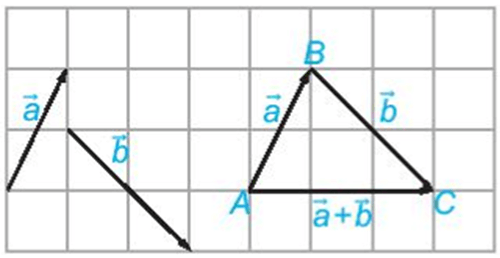
- Quy tắc ba điểm: Với ba điểm bất kì A, B, C, ta có ![]() +
+ ![]() =
= ![]() .
.
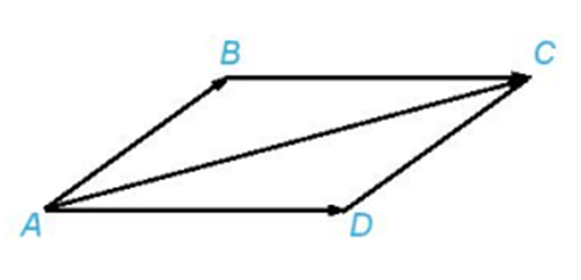
- Quy tắc hình bình hành: Nếu ABCD là hình bình hành thì ![]() +
+ ![]() =
= ![]() .
.
– Với ba vectơ; ![]() ,
, ![]() ,
, ![]() tùy ý :
tùy ý :
+ Tính chất giao hoán: ![]() +
+ ![]() =
= ![]() +
+ ![]() ;
;
+ Tính chất kết hợp: (![]() +
+ ![]() ) +
) + ![]() =
= ![]() + (
+ (![]() +
+ ![]() );
);
+ Tính chất của vectơ–không: ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() .
.
Chú ý: Do các vectơ (![]() +
+ ![]() ) +
) + ![]() và
và ![]() + (
+ (![]() +
+ ![]() ) bằng nhau, nên ta còn viết chúng dưới dạng
) bằng nhau, nên ta còn viết chúng dưới dạng ![]() +
+ ![]() +
+ ![]() và gọi là tổng của ba vectơ
và gọi là tổng của ba vectơ ![]() ,
, ![]() ,
, ![]() . Tương tự, ta cũng có thể viết tổng của một số vectơ mà không cần dùng dấu ngoặc.
. Tương tự, ta cũng có thể viết tổng của một số vectơ mà không cần dùng dấu ngoặc.
4. Hiệu của hai vectơ
- Vectơ có cùng độ dài và ngược hướng với vectơ ![]() được gọi là vectơ đối của vectơ
được gọi là vectơ đối của vectơ ![]() . Vectơ đối của vectơ
. Vectơ đối của vectơ ![]() kí hiệu là -
kí hiệu là -![]() .
.
- Vectơ được coi là vectơ đối của chính nó.
- Hai vectơ đối nhau khi và chỉ khi tổng của chúng bằng ![]() .
.
- Vectơ ![]() + (-
+ (-![]() ) được gọi là hiệu của hai vectơ
) được gọi là hiệu của hai vectơ ![]() và
và ![]() và được kí hiệu là
và được kí hiệu là ![]() -
- ![]() . Phép lấy hiệu hai vectơ được gọi là phép trừ vectơ.
. Phép lấy hiệu hai vectơ được gọi là phép trừ vectơ.
- Nếu ![]() +
+ ![]() =
= ![]() thì
thì ![]() -
- ![]() =
= ![]() + (-
+ (-![]() ) =
) = ![]() +
+ ![]() + (-
+ (-![]() ) =
) = ![]() +
+ ![]() =
= ![]() .
.
- Quy tắc hiệu: Với ba điểm O, M, N, ta có 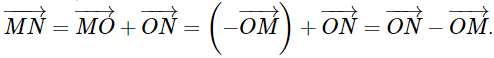
5. Tích của một vectơ với một số
• Tích của một vectơ ![]() ≠
≠ ![]() với một số thực k > 0 là một vectơ, kí hiệu là k
với một số thực k > 0 là một vectơ, kí hiệu là k![]() , cùng hướng với vectơ
, cùng hướng với vectơ ![]() và có độ dài bằng k
và có độ dài bằng k![]() .
.
6. Các tính chất của phép nhân vectơ với một số
Với hai vectơ ![]() ,
, ![]() và hai số thực k, t, ta luôn có :
và hai số thực k, t, ta luôn có :
+) k(t![]() ) = (kt)
) = (kt) ![]() ;
;
+) k (![]() +
+ ![]() ) = k
) = k![]() + k
+ k![]() ; k (
; k (![]() –
– ![]() ) = k
) = k![]() – k
– k![]() ;
;
+) (k + t) ![]() = k
= k![]() + t
+ t![]() ;
;
+) 1![]() =
= ![]() ; (–1)
; (–1) ![]() = –
= –![]() .
.
7. Góc giữa hai vectơ
Cho hai vectơ ![]() và
và ![]() khác
khác ![]() . Từ một điểm A tùy ý, vẽ các vectơ
. Từ một điểm A tùy ý, vẽ các vectơ ![]() =
= ![]() và
và ![]() =
= ![]() . Khi đó, số đo của góc BAC được gọi là số đo góc giữa hai vectơ
. Khi đó, số đo của góc BAC được gọi là số đo góc giữa hai vectơ ![]() và
và ![]() hay đơn giản là góc giữa hai vectơ
hay đơn giản là góc giữa hai vectơ ![]() ,
, ![]() , kí hiệu là (
, kí hiệu là (![]() ,
, ![]() ).
).
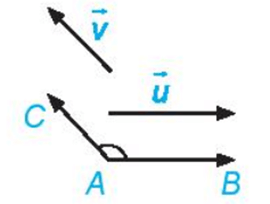
Chú ý :
+ Quy ước rằng góc giữa hai vectơ ![]() và
và ![]() có thể nhận một giá trị tùy ý từ 0° đến 180°.
có thể nhận một giá trị tùy ý từ 0° đến 180°.
+ Nếu (![]() ,
, ![]() ) = 90° thì ta nói rằng
) = 90° thì ta nói rằng ![]() và
và ![]() vuông góc với nhau. Kí hiệu
vuông góc với nhau. Kí hiệu ![]() ⊥
⊥ ![]() hoặc
hoặc ![]() ⊥
⊥ ![]() . Đặc biệt được coi là vuông góc với mọi vectơ.
. Đặc biệt được coi là vuông góc với mọi vectơ.
8. Tích vô hướng của hai vectơ
Tích vô hướng của hai vectơ khác vectơ-không ![]() và
và ![]() là một số, kí hiệu là
là một số, kí hiệu là ![]() .
.![]() , được xác định bởi công thức sau:
, được xác định bởi công thức sau:
![]() .
. ![]() = |
= |![]() |.|
|.|![]() |.cos(
|.cos(![]() ,
, ![]() )
)
Chú ý:
+) ![]() ⊥
⊥ ![]() ⇔
⇔ ![]() .
. ![]() = 0.
= 0.
+) ![]() .
. ![]() còn được viết là
còn được viết là ![]() 2 và được gọi là bình phương vô hướng của vectơ
2 và được gọi là bình phương vô hướng của vectơ ![]() .
.
Ta có ![]() 2 = |
2 = |![]() |.|
|.|![]() |.cos0o = (
|.cos0o = (![]() )2.
)2.
(Bình phương vô hướng của một vectơ bằng bình phương độ dài của vectơ đó.)
9. Biểu thức tọa độ và tính chất của tích vô hướng
• Tích vô hướng của hai vectơ ![]() = (x;y) và
= (x;y) và ![]() = (x';y') được tính theo công thức :
= (x';y') được tính theo công thức :
![]() .
. ![]() = x.x' + y.y'.
= x.x' + y.y'.
Nhận xét:
+ Hai vectơ ![]() và
và ![]() vuông góc với nhau khi và chỉ khi x.x' + y.y' = 0.
vuông góc với nhau khi và chỉ khi x.x' + y.y' = 0.
+ Bình phương vô hướng của ![]() = (x;y) là
= (x;y) là ![]() 2 = x2 + y2.
2 = x2 + y2.
+ Nếu ![]() ≠
≠ ![]() và
và ![]() ≠
≠ ![]() thì
thì 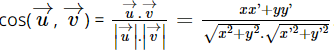 .
.
• Tính chất của tích vô hướng :
Với ba vectơ ![]() ,
, ![]() ,
, ![]() bất kì và mọi số thực k, ta có :
bất kì và mọi số thực k, ta có :
+) ![]() .
. ![]() =
= ![]() .
. ![]() (tính chất giao hoán);
(tính chất giao hoán);
+) ![]() . (
. (![]() +
+ ![]() ) =
) = ![]() .
. ![]() +
+ ![]() .
. ![]() (tính chất phân phối đối với phép cộng) ;
(tính chất phân phối đối với phép cộng) ;
+) (k ![]() ).
). ![]() = k (
= k (![]() .
. ![]() ) =
) = ![]() .( k
.( k![]() ).
).
Chú ý: Từ tính trên, ta có thể chứng minh được :
![]() . (
. (![]() –
– ![]() )=
)= ![]() .
. ![]() –
– ![]() .
. ![]() (tính chất phân phối đối với phép trừ) ;
(tính chất phân phối đối với phép trừ) ;
(![]() +
+ ![]() )2 =
)2 = ![]() 2 + 2
2 + 2![]() .
. ![]() +
+ ![]() 2; (
2; (![]() –
– ![]() )2 =
)2 = ![]() 2 –2
2 –2![]() .
.![]() +
+ ![]() 2;
2;
(![]() +
+ ![]() ).(
).(![]() –
– ![]() ) =
) = ![]() 2 –
2 – ![]() 2.
2.
Bài tập
Câu 1: Trong mặt phẳng tọa độ, cặp vectơ nào sau đây có cùng phương?
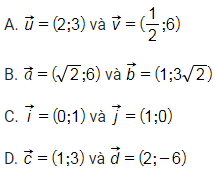
Phương pháp giải:
Cho ![]() = (x;y) và
= (x;y) và ![]() = (z,t) (z,t # 0)
= (z,t) (z,t # 0)
+) Nếu ![]() thì
thì ![]() và
và ![]() cùng phương
cùng phương
+) Nếu ![]() thì
thì ![]() và
và ![]() không cùng phương.
không cùng phương.
Lời giải:
A. Ta có: 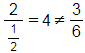 nên
nên ![]() và
và ![]() không cùng phương.
không cùng phương.
B. Ta có: 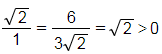 nên
nên ![]() và
và ![]() cùng phương, hơn nữa là cùng hướng
cùng phương, hơn nữa là cùng hướng
Chọn đáp án B.
C. Ta có: ![]()
Vậy ![]() và
và ![]() không cùng phương.
không cùng phương.
D. Ta có: ![]() nên
nên ![]() và
và ![]() không cùng phương.
không cùng phương.
Câu 2: Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?
A. ![]() = (2;3) và
= (2;3) và 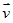 = (4;6)
= (4;6)
B. ![]() = (1;-1) và
= (1;-1) và ![]() = (-1;1)
= (-1;1)
C. ![]() = (a;b) và
= (a;b) và ![]() = (-b;a)
= (-b;a)
D. ![]() = (1;1) và
= (1;1) và ![]() = (2;0)
= (2;0)
Phương pháp giải:
+) Cho ![]() (x;y),
(x;y), 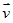 (z;t) thì
(z;t) thì ![]() .
.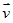 = x.z + y.t
= x.z + y.t
+) ![]()
Lời giải:
A. Ta có: ![]() .
.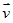 = 2.4 + 3.6 = 26 ≠ 0 nên
= 2.4 + 3.6 = 26 ≠ 0 nên ![]() và
và 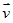 không vuông góc với nhau.
không vuông góc với nhau.
B. Ta có: ![]() .
.![]() = 1.(-1) + (-1).1 = -2 ≠ 0 nên
= 1.(-1) + (-1).1 = -2 ≠ 0 nên ![]() và
và ![]() không vuông góc với nhau.
không vuông góc với nhau.
C. Ta có: ![]() .
.![]() = a.(-b) + b.a = 0 nên
= a.(-b) + b.a = 0 nên ![]() và
và ![]() vuông góc với nhau.
vuông góc với nhau.
Chọn đáp án C
D. Ta có: ![]() .
.![]() = 1.2 + 1.0 = 2 ≠ 0 nên
= 1.2 + 1.0 = 2 ≠ 0 nên ![]() và
và ![]() không vuông góc với nhau.
không vuông góc với nhau.
Câu 3: Trong mặt phẳng tọa độ, vectơ nào sau đây có độ dài bằng 1?
A. ![]() = (1;1)
= (1;1)
B. ![]() = (1;-1)
= (1;-1)
C. ![]() = (2;
= (2;![]() )
)
D. ![]() = (
= (![]() ;-
;-![]() )
)
Phương pháp giải:
Tính độ dài vectơ ![]() (x;y) theo công thức:
(x;y) theo công thức: ![]() .
.
Lời giải:
A. Ta có: ![]() . (Loại)
. (Loại)
B. Ta có: ![]() . (Loại)
. (Loại)
C. Ta có: ![]() . (Loại)
. (Loại)
D. Ta có: 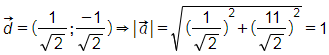 . (Thỏa mãn yc)
. (Thỏa mãn yc)
Chọn D
Câu 4: Góc giữa vectơ ![]() = (1;-1) và vectơ
= (1;-1) và vectơ ![]() = (-2;0) có số đo bằng:
= (-2;0) có số đo bằng:
A. 90o
B. 0o
C. 135o
D. 45o
Phương pháp giải:
Tính ![]() .
.![]() .
.
+) Nếu ![]() .
.![]() = 0 thì góc giữa 2 vectơ bằng 90o.
= 0 thì góc giữa 2 vectơ bằng 90o.
+) Nếu ![]() .
.![]() ≠ 0 thì
≠ 0 thì 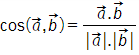
Lời giải:
Ta có: ![]() .
.![]() = 1.(-2) + (-1).0 = -2 ≠ 0.
= 1.(-2) + (-1).0 = -2 ≠ 0.
Lại có: ![]()
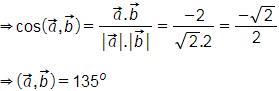
Chọn C
Câu 5: Khẳng định nào sau đây là đúng?
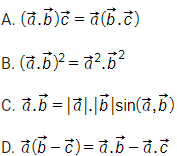
Phương pháp giải:
+) ![]()
Lời giải:
Chọn D. Đây là một tính chất của tích vô hướng.
A. Sai vì ![]()
B. Sai vì ![]()
C. Sai vì ![]()
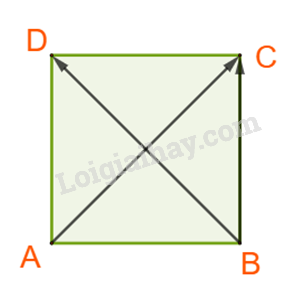
Câu 6: Cho hình vuông ABCD có cạnh a. Khẳng định nào sau đây là đúng?
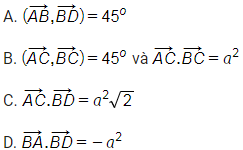
Phương pháp giải:
Tính tích vô hướng bằng công thức: ![]() .
.
Lời giải:
A. Ta có: ![]() Vậy A sai.
Vậy A sai.
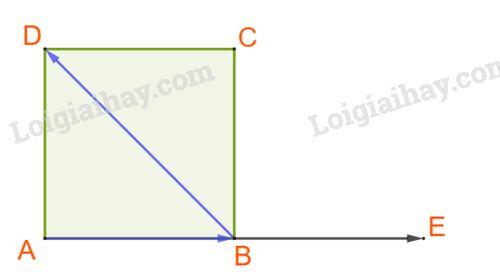
B. Ta có:
![]()
Vậy B đúng.
Chọn B
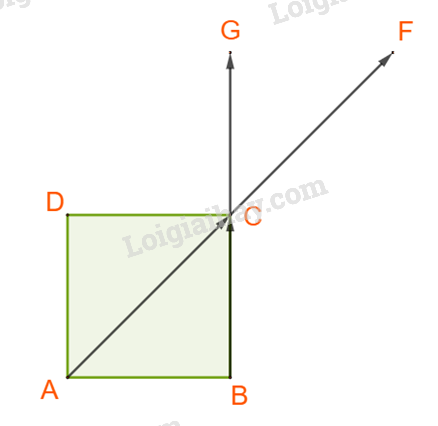
C. Dễ thấy ![]() Vậy C sai.
Vậy C sai.
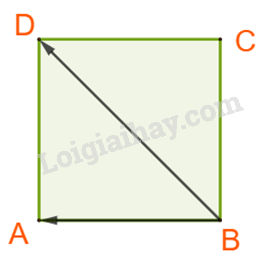
D. Ta có:
![]() Vậy D sai.
Vậy D sai.
Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 11: Tích vô hướng của hai vecto
Bài 13: Các số đặc trưng đo xu thế trung tâm
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.