Toán 10 Kết nối tri thức: Bài tập cuối chương 4

Phương Thảo Ngày: 12-02-2023 Lớp 10

689

Toptailieu.vn giới thiệu Giải SGK Toán 10 Bài tập cuối chương 4 (Kết nối tri thức) giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:

Toán 10 Kết nối tri thức: Bài tập cuối chương 4

Câu hỏi trang 71 Toán 10

Bài 4.27 trang 71 Toán 10: Trong mặt phẳng tọa độ, cặp vectơ nào saua đây có cùng phương?

A. $\vec{u} = (2; 3)$ và $\vec{v} = (\frac{1}{2}; 6)$

B. $\vec{a} = (\sqrt{2}; 6)$ và $\vec{b} = (1; 3 \sqrt{2})$

C. $\vec{i} = (0; 1)$ và $\vec{j} = (1; 0)$

D. $\vec{c} = (1; 3)$ và $\vec{d} = (2; - 6)$

Phương pháp giải:

Cho $\vec{a} = (x; y)$ và $\vec{b} = (z, t)$ ( $z, t \neq 0$ )

+) Nếu $\frac{x}{z} = \frac{y}{t} = k$ thì $\vec{a}$ và $\vec{b}$ cùng phương

+) Nếu $\frac{x}{z} \neq \frac{y}{t}$ thì $\vec{a}$ và $\vec{b}$ không cùng phương.

Lời giải:

A. Ta có: $\frac{2}{\frac{1}{2}} = 4 \neq \frac{3}{6}$ nên $\vec{u}$ và $\vec{v}$ không cùng phương.

B. Ta có: $\frac{\sqrt{2}}{1} = \frac{6}{3 \sqrt{2}} = \sqrt{2} > 0$ nên $\vec{a}$ và $\vec{b}$ cùng phương, hơn nữa là cùng hướng

Chọn đáp án B.

C. Ta có: $\vec{i} . \vec{j} = 0.1 + 1.0 = 0 \Rightarrow \vec{i} ⊥ \vec{j}$

Vậy $\vec{i}$ và $\vec{j}$ không cùng phương.

D. Ta có: $\frac{1}{2} \neq \frac{3}{- 6}$ nên $\vec{c}$ và $\vec{d}$ không cùng phương.

Bài 4.28 trang 71 Toán 10: Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?

A. $\vec{u} = (2; 3)$ và $\vec{v} = (4; 6)$

B. $\vec{a} = (1; - 1)$ và $\vec{b} = (- 1; 1)$

C. $\vec{z} = (a; b)$ và $\vec{t} = (- b; a)$

D. $\vec{n} = (1; 1)$ và $\vec{k} = (2; 0)$

Phương pháp giải:

+) Cho $\vec{u} (x; y), \vec{v} (z; t)$ thì $\vec{u} . \vec{v} = x . z + y . t$

+) $\vec{u} ⊥ \vec{v} \Leftrightarrow \vec{u} . \vec{v} = 0$

Lời giải:

A. Ta có: $\vec{u} . \vec{v} = 2.4 + 3.6 = 26 \neq 0$ nên $\vec{u}$ và $\vec{v}$ không vuông góc với nhau.

B. Ta có: $\vec{a} . \vec{b} = 1. (- 1) + (- 1) .1 = - 2 \neq 0$ nên $\vec{a}$ và $\vec{b}$ không vuông góc với nhau.

C. Ta có: $\vec{z} . \vec{t} = a . (- b) + b . a = 0$ nên $\vec{z}$ và $\vec{t}$ vuông góc với nhau.

Chọn đáp án C

D. Ta có: $\vec{n} . \vec{k} = 1.2 + 1.0 = 2 \neq 0$ nên $\vec{n}$ và $\vec{k}$ không vuông góc với nhau.

Bài 4.29 trang 71 Toán 10: Trong mặt phẳng tọa độ, vectơ nào sau đây có độ dài bằng 1?

A. $\vec{a} = (1; 1)$

B. $\vec{b} = (1; - 1)$

C. $\vec{c} = (2; \frac{1}{2})$

D. $\vec{d} = (\frac{1}{\sqrt{2}}; \frac{- 1}{\sqrt{2}})$

Phương pháp giải:

Tính độ dài vectơ $\vec{a} (x; y)$ theo công thức: $| \vec{a} | = \sqrt{x^{2} + y^{2}}$ .

Lời giải:

A. Ta có: $\vec{a} = (1; 1) \Rightarrow | \vec{a} | = \sqrt{1^{2} + 1^{2}} = \sqrt{2} \neq 1$ . (Loại)

B. Ta có: $\vec{b} = (1; - 1) \Rightarrow | \vec{b} | = \sqrt{1^{2} + {(- 1)}^{2}} = \sqrt{2} \neq 1$ . (Loại)

C. Ta có: $\vec{c} = (2; \frac{1}{2}) \Rightarrow | \vec{c} | = \sqrt{2^{2} + {(\frac{1}{2})}^{2}} = \frac{\sqrt{17}}{2} \neq 1$ . (Loại)

D. Ta có: $\vec{d} = (\frac{1}{\sqrt{2}}; \frac{- 1}{\sqrt{2}}) \Rightarrow | \vec{a} | = \sqrt{{(\frac{1}{\sqrt{2}})}^{2} + {(\frac{11}{\sqrt{2}})}^{2}} = 1$ . (Thỏa mãn yc)

Chọn D

Bài 4.30 trang 71 Toán 10: Góc giữa vectơ $\vec{a} = (1; - 1)$ và vectơ $\vec{b} = (- 2; 0)$ có số đo bằng:

A. $90^{o}$

B. $0^{o}$

C. $135^{o}$

D. $45^{o}$

Phương pháp giải:

Tính $\vec{a} . \vec{b}$ .

+) Nếu $\vec{a} . \vec{b} = 0$ thì góc giữa 2 vectơ bằng $90^{o}$ .

+) Nếu $\vec{a} . \vec{b} \neq 0$ thì $\cos (\vec{a}, \vec{b}) = \frac{\vec{a} . \vec{b}}{| \vec{a} | . | \vec{b} |}$

Lời giải:

Ta có: $\vec{a} . \vec{b} = 1. (- 2) + (- 1) .0 = - 2 \neq 0$ .

Lại có: $| \vec{a} | = \sqrt{1^{2} + {(- 1)}^{2}} = \sqrt{2}; | \vec{b} | = \sqrt{{(- 2)}^{2} + 0^{2}} = 2.$

$\Rightarrow \cos (\vec{a}, \vec{b}) = \frac{\vec{a} . \vec{b}}{| \vec{a} | . | \vec{b} |} = \frac{- 2}{\sqrt{2} .2} = \frac{- \sqrt{2}}{2}$

$\Rightarrow (\vec{a}, \vec{b}) = 135^{o}$

Chọn C

Bài 4.31 trang 71 Toán 10: Khẳng định nào sau đây là đúng?

A. $(\vec{a} . \vec{b}) \vec{c} = \vec{a} (\vec{b} . \vec{c})$

B. $(\vec{a} . \vec{b})^{2} = {\vec{a}}^{2} . {\vec{b}}^{2}$

C. $\vec{a} . \vec{b} = | \vec{a} | . | \vec{b} | \sin (\vec{a}, \vec{b})$

D. $\vec{a} (\vec{b} - \vec{c}) = \vec{a} . \vec{b} - \vec{a} . \vec{c}$

Phương pháp giải:

+) $\vec{a} . \vec{b} = | \vec{a} | . | \vec{b} | \cos (\vec{a}, \vec{b})$

Lời giải:

Chọn D. Đây là một tính chất của tích vô hướng.

A. Sai vì $(\vec{a} . \vec{b}) \vec{c} = [| \vec{a} | . | \vec{b} | \cos (\vec{a}, \vec{b})] . \vec{c} \neq$ $\vec{a} (\vec{b} . \vec{c}) = \vec{a} [| \vec{b} | . | \vec{c} | \cos (\vec{b}, \vec{c})]$

B. Sai vì $(\vec{a} . \vec{b})^{2} = [\vec{a} . \vec{b} = | \vec{a} | . | \vec{b} | \cos (\vec{a}, \vec{b})]^{2} = {\vec{a}}^{2} . {\vec{b}}^{2} . \cos^{2} (\vec{a}, \vec{b})$ $\neq {\vec{a}}^{2} . {\vec{b}}^{2}$

C. Sai vì $\vec{a} . \vec{b} = | \vec{a} | . | \vec{b} | \cos (\vec{a}, \vec{b}) \neq | \vec{a} | . | \vec{b} | \sin (\vec{a}, \vec{b})$

Bài 4.32 trang 71 Toán 10: Cho hình vuông ABCD có cạnh a. Khẳng định nào sau đây là đúng?

A. $(\vec{A B}, \vec{B D}) = 45^{o}$

B. $(\vec{A C}, \vec{B C}) = 45^{o}$ và $\vec{A C} . \vec{B C} = a^{2}$

C. $\vec{A C} . \vec{B D} = a^{2} \sqrt{2}$

D. $\vec{B A} . \vec{B D} = - a^{2}$

Phương pháp giải:

Tính tích vô hướng bằng công thức: $\vec{a} . \vec{b} = | \vec{a} | . | \vec{b} | \cos (\vec{a}, \vec{b})$ .

Lời giải:

A. Ta có: $(\vec{A B}, \vec{B D}) = (\vec{B E}, \vec{B D}) = 135^{o} \neq 45^{o} .$ Vậy A sai.

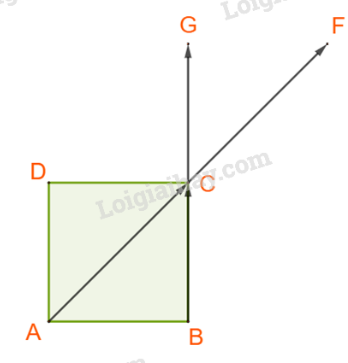
Bài 4.32 trang 71 Toán 10 Tập 1 I Kết nối tri thức (ảnh 4)

B. Ta có: $(\vec{A C}, \vec{B C}) = (\vec{C F}, \vec{C G}) = 45^{o}$ và $\vec{A C} . \vec{B C} = A C . B C . \cos 45^{o} = a \sqrt{2} . a . \frac{\sqrt{2}}{2} = a^{2} .$

Vậy B đúng.

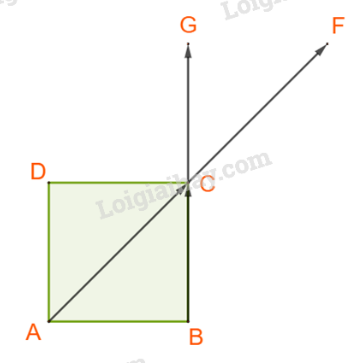
Bài 4.32 trang 71 Toán 10 Tập 1 I Kết nối tri thức (ảnh 3)

Chọn B

C. Dễ thấy $A C ⊥ B D$ nên $\vec{A C} . \vec{B D} = 0 \neq a^{2} \sqrt{2} .$ Vậy C sai.

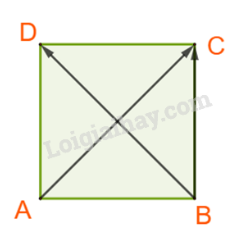
Bài 4.32 trang 71 Toán 10 Tập 1 I Kết nối tri thức (ảnh 2)

D. Ta có: $(\vec{B A} . \vec{B D}) = 45^{o}$ $\Rightarrow \vec{B A} . \vec{B D} = B A . B D . \cos 45^{o} = a . a \sqrt{2} . \frac{\sqrt{2}}{2} = a^{2} \neq - a^{2} .$ Vậy D sai.

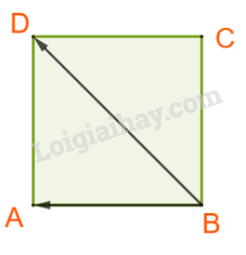
Bài 4.32 trang 71 Toán 10 Tập 1 I Kết nối tri thức (ảnh 1)

Bài 4.33 trang 71 Toán 10: Trên cạnh BC của tam giác ABC lấy điểm M sao cho MB = 3 MC.

a) Tìm mối liên hệ giữa hai vectơ $\vec{M B}$ và $\vec{M C}$

b) Biểu thị vectơ $\vec{A M}$ theo hai vectơ $\vec{A B}$ và $\vec{A C}$ .

Phương pháp giải:

+) Nếu $M B = k . M C$ và $\vec{M B}$ và $\vec{M C}$ ngược hướng thì $\vec{M B} = - k . \vec{M C}$

+) $\vec{A M} = \vec{A B} + \vec{B M}$ (quy tắc cộng)

+) $\vec{B C} = \vec{A C} - \vec{A B}$ (quy tắc hiệu)

Lời giải:

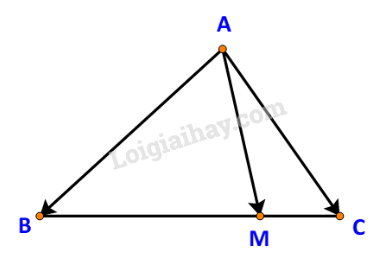
Bài 4.33 trang 71 Toán 10 Tập 1 I Kết nối tri thức (ảnh 1)

a) M thuộc cạnh BC nên vectơ $\vec{M B}$ và $\vec{M C}$ ngược hướng với nhau.

Lại có: MB = 3 MC $\Rightarrow \vec{M B} = - 3. \vec{M C}$

b) Ta có: $\vec{A M} = \vec{A B} + \vec{B M}$

Mà $B M = \frac{3}{4} B C$ nên $\vec{B M} = \frac{3}{4} \vec{B C}$

$\Rightarrow \vec{A M} = \vec{A B} + \frac{3}{4} \vec{B C}$

Lại có: $\vec{B C} = \vec{A C} - \vec{A B}$ (quy tắc hiệu)

$\Rightarrow \vec{A M} = \vec{A B} + \frac{3}{4} (\vec{A C} - \vec{A B}) = \frac{1}{4} . \vec{A B} + \frac{3}{4} . \vec{A C}$

Vậy $\vec{A M} = \frac{1}{4} . \vec{A B} + \frac{3}{4} . \vec{A C}$

Câu hỏi trang 72 Toán 10

Bài 4.34 trang 72 Toán 10: Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có:

$\vec{M A} + \vec{M C} = \vec{M B} + \vec{M D}$ .

Phương pháp giải:

+) ABCD là hình bình hành thì: $\vec{A B} = \vec{D C}$

Lời giải:

Do ABCD là hình bình hành nên $\vec{A B} = \vec{D C}$

$\begin{array}{l} \Rightarrow \vec{A M} + \vec{M B} = \vec{D M} + \vec{M C} \\ \Leftrightarrow - \vec{M A} + \vec{M B} = - \vec{M D} + \vec{M C} \\ \Leftrightarrow \vec{M A} + \vec{M C} = \vec{M B} + \vec{M D} \end{array}$

Cách 2:

Ta có: $\vec{M A} + \vec{M C} = \vec{M B} + \vec{M D} \Leftrightarrow \vec{M A} - \vec{M B} = \vec{M D} - \vec{M C}$ (*)

Áp dụng quy tắc hiệu ta có: $\vec{M A} - \vec{M B} = \vec{B A}; \vec{M D} - \vec{M C} = \vec{C D}$

Do đó (*) $\Leftrightarrow \vec{B A} = \vec{C D}$ (luôn đúng do ABCD là hình bình hành)

Cách 3:

Ta có:

$\vec{M A} + \vec{M C} = \vec{M B} + \vec{B A} + \vec{M D} + \vec{D C} = \vec{M B} + \vec{M D} + (\vec{B A} + \vec{D C})$

Vì ABCD là hình bình hành nên $\vec{A B} = \vec{D C}$ $\Rightarrow - \vec{B A} = \vec{D C}$ hay $\vec{B A} + \vec{D C} = \vec{0}$

$\Rightarrow \vec{M A} + \vec{M C} = \vec{M B} + \vec{M D}$ (đpcm)

Bài 4.35 trang 72 Toán 10: Trong mặt phẳng tọa độ Oxy, cho A (2; 1), B (-2; 5) và C (-5; 2).

a) Tìm tọa độ của các vectơ $\vec{B A}$ và $\vec{B C}$

b) Chứng minh rằng A, B, C là ba đỉnh của một tam giác vuông. Tính diện tích và chu vi của tam giác đó.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

d) Tìm tọa độ của điểm D sao cho tứ giác BCAD là một hình bình hành.

Phương pháp giải:

a) Tọa độ của vectơ: $\vec{B A} = (x_{A} - x_{B}; y_{A} - y_{B})$

b) Tính $\vec{B A} . \vec{B C} = 0$ , chỉ ra góc vuông trong tam giác ABC.

c) Công thức tọa độ của trọng tâm G là $(\frac{x_{A} + x_{B} + x_{C}}{3}; \frac{y_{A} + y_{B} + y_{C}}{3})$

d) BCAD là một hình bình hành $\Leftrightarrow \vec{B C} = \vec{A D}$

Lời giải:

a) Ta có: $\vec{B A} = (2 - (- 2); 1 - 5) = (4; - 4)$ và $\vec{B C} = (- 5 - (- 2); 2 - 5) = (- 3; - 3)$

b) Ta có: $\vec{B A} . \vec{B C} = 4. (- 3) + (- 4) . (- 3) = 0$

$\Rightarrow \vec{B A} ⊥ \vec{B C}$ hay $\hat{A B C} = 90^{o}$

Vậy tam giác ABC vuông tại B.

Lại có: $A B = | \vec{B A} | = \sqrt{4^{2} + {(- 4)}^{2}} = 4 \sqrt{2}$ ; $B C = | \vec{B C} | = \sqrt{3^{2} + {(- 3)}^{2}} = 3 \sqrt{2}$

Và $A C = \sqrt{A B^{2} + B C^{2}} = 5 \sqrt{2}$ (do $Δ A B C$ vuông tại B).

Diện tích tam giác ABC là: $S_{A B C} = \frac{1}{2} . A B . B C = \frac{1}{2} .4 \sqrt{2} .3 \sqrt{2} = 12$

Chu vi tam giác ABC là: $A B + B C + A C = 4 \sqrt{2} + 3 \sqrt{2} + 5 \sqrt{2} = 12 \sqrt{2}$

c) Tọa độ của trọng tâm G là $(\frac{2 + (- 2) + (- 5)}{3}; \frac{1 + 5 + 2}{3}) = (\frac{- 5}{3}; \frac{8}{3})$

d) Giả sử điểm D thỏa mãn BCAD là một hình bình hành có tọa độ là (a; b).

Ta có: $\vec{B C} = (- 3; - 3)$ và $\vec{A D} = (a - 2; b - 1)$

Vì BCAD là một hình bình hành nên $\vec{A D} = \vec{B C}$

$\begin{array}{l} \Leftrightarrow (a - 2; b - 1) = (- 3; - 3) \\ \Leftrightarrow {\begin{cases} a - 2 = - 3 \\ b - 1 = - 3 \end{cases} \Leftrightarrow {\begin{cases} a = - 1 \\ b = - 2 \end{cases} \end{array}$

Vậy D có tọa độ (-1; -2)

Bài 4.36 trang 72 Toán 10: Trong mặt phẳng tọa độ Oxy, cho A (1; 2), B (3; 4), C (-1; -2) và D (6;5).

a) Hãy tìm tọa độ của các vectơ $\vec{A B}$ và $\vec{C D}$

b) Hãy giải thích tại sao các vectơ $\vec{A B}$ và $\vec{C D}$ cùng phương.

c) Giả sử E là điểm có tọa độ (a; 1). Tìm a để các vectơ $\vec{A C}$ và $\vec{B E}$ cùng phương.

d) Với a tìm được, hãy biểu thị vectơ $\vec{A E}$ theo các vectơ $\vec{A B}$ và $\vec{A C}$ .

Phương pháp giải:

a) Tọa độ của vectơ: $\vec{A B} = (x_{B} - x_{A}; y_{B} - y_{A})$

b) Tìm $k \neq 0$ sao cho: $\vec{A B} = k . \vec{C D}$

c) Vectơ $\vec{u} (a; b)$ và $\vec{v} (x; y)$ $(x; y \neq 0)$ cùng phương $\Leftrightarrow \frac{a}{x} = \frac{b}{y}$ $(x; y \neq 0)$

Lời giải:

a) Ta có: $\vec{A B} = (3 - 1; 4 - 2) = (2; 2)$ và $\vec{C D} = (6 - (- 1); 5 - (- 2)) = (7; 7)$

b) Dễ thấy: $(2; 2) = \frac{2}{7} . (7; 7)$ $\Rightarrow \vec{A B} = \frac{2}{7} . \vec{C D}$

Vậy hai vectơ $\vec{A B}$ và $\vec{C D}$ cùng phương.

c) Ta có: $\vec{A C} = (- 1 - 1; - 2 - 2) = (- 2; - 4)$ và $\vec{B E} = (a - 3; 1 - 4) = (a - 3; - 3)$

Để $\vec{A C}$ và $\vec{B E}$ cùng phương thì $\frac{a - 3}{- 2} = \frac{- 3}{- 4}$ $\Leftrightarrow a - 3 = - \frac{3}{2}$ $\Leftrightarrow a = \frac{3}{2}$

Vậy $a = \frac{3}{2}$ hay $E (\frac{3}{2}; 1)$ thì hai vectơ $\vec{A C}$ và $\vec{B E}$ cùng phương

d) Cách 1:

Ta có: $\vec{B E} = (\frac{3}{2} - 3; - 3) = (- \frac{3}{2}; - 3)$ ; $\vec{A C} = (- 2; - 4)$

$\Rightarrow \vec{B E} = \frac{3}{4} . \vec{A C}$

Mà $\vec{A E} = \vec{A B} + \vec{B E}$ (quy tắc cộng)

$\Rightarrow \vec{A E} = \vec{A B} + \frac{3}{4} . \vec{A C}$

Cách 2:

Giả sử $\vec{A E} = m . \vec{A B} + n . \vec{A C}$ (*)

Ta có: $\vec{A E} = (\frac{1}{2}; - 1)$ , $m . \vec{A B} = m (2; 2) = (2 m; 2 m)$ , $n . \vec{A C} = n (- 2; - 4) = (- 2 n; - 4 n)$

Do đó (*) $\Leftrightarrow (\frac{1}{2}; - 1) = (2 m; 2 m) + (- 2 n; - 4 n)$

$\begin{array}{l} \Leftrightarrow (\frac{1}{2}; - 1) = (2 m - 2 n; 2 m - 4 n) \\ \Leftrightarrow {\begin{cases} \frac{1}{2} = 2 m - 2 n \\ - 1 = 2 m - 4 n \end{cases} \Leftrightarrow {\begin{cases} m = 1 \\ n = \frac{3}{4} \end{cases} \end{array}$

Vậy $\vec{A E} = \vec{A B} + \frac{3}{4} . \vec{A C}$

Bài 4.37 trang 72 Toán 10: Cho vectơ $\vec{a} \neq \vec{0}$ . Chứng minh rằng $\frac{1}{| \vec{a} |} \vec{a}$ (hay còn được viết là $\frac{\vec{a}}{| \vec{a} |}$ ) là một vectơ đơn vị, cùng hướng với vectơ $\vec{a}$ .

Lời giải:

Cách 1:

Gọi tọa độ của vectơ $\vec{a}$ là (x; y).

Ta có: $| \vec{a} | = \sqrt{x^{2} + y^{2}}$ .

Đặt $\vec{i} = \frac{1}{| \vec{a} |} . \vec{a}$

$\Rightarrow \vec{i} = \frac{1}{\sqrt{x^{2} + y^{2}}} . (x; y) = (\frac{x}{\sqrt{x^{2} + y^{2}}}; \frac{y}{\sqrt{x^{2} + y^{2}}})$

$\Rightarrow | \vec{i} | = \sqrt{{(\frac{x}{\sqrt{x^{2} + y^{2}}})}^{2} + {(\frac{y}{\sqrt{x^{2} + y^{2}}})}^{2}} = \sqrt{\frac{x^{2}}{x^{2} + y^{2}} + \frac{y^{2}}{x^{2} + y^{2}}} = 1$

Mặt khác:

$\vec{i} = \frac{1}{| \vec{a} |} . \vec{a} = \frac{1}{\sqrt{x^{2} + y^{2}}} . \vec{a}$ và $\frac{1}{\sqrt{x^{2} + y^{2}}} > 0$ với mọi $x, y \neq 0$

Do đó vectơ $\vec{i}$ và $\vec{a}$ cùng hướng.

Vậy $\frac{1}{| \vec{a} |} \vec{a}$ (hay $\frac{\vec{a}}{| \vec{a} |}$ ) là một vectơ đơn vị, cùng hướng với vectơ $\vec{a}$ .

Cách 2:

Với mọi vectơ $\vec{a} \neq \vec{0}$ , ta có: $| \vec{a} | > 0 \Rightarrow k = \frac{1}{| \vec{a} |} > 0$ . Đặt $\vec{i} = \frac{1}{| \vec{a} |} . \vec{a} = k . \vec{a}$

$\begin{array}{l} \Rightarrow | \vec{i} | = | k . \vec{a} | = | k | . | \vec{a} | \\ \Leftrightarrow | \vec{i} | = k . | \vec{a} | = \frac{1}{| \vec{a} |} . | \vec{a} | = 1 \end{array}$

Mặt khác: $\vec{i} = \frac{1}{| \vec{a} |} . \vec{a} = k . \vec{a}$ và $k > 0$

Do đó vectơ $\vec{i}$ và $\vec{a}$ cùng hướng.

Vậy $\frac{1}{| \vec{a} |} \vec{a}$ (hay $\frac{\vec{a}}{| \vec{a} |}$ ) là một vectơ đơn vị, cùng hướng với vectơ $\vec{a}$ .

Bài 4.38 trang 72 Toán 10: Cho ba vectơ $\vec{a}, \vec{b}, \vec{u}$ với $| \vec{a} | = | \vec{b} | = 1$ và $\vec{a} ⊥ \vec{b}$ . Xét một hệ trục Oxy với các vectơ đơn vị $\vec{i} = \vec{a}, \vec{j} = \vec{b} .$ Chứng minh rằng:

a) Vectơ $\vec{u}$ có tọa độ là $(\vec{u} . \vec{a}; \vec{u} . \vec{b})$

b) $\vec{u} = (\vec{u} . \vec{a}) . \vec{a} + (\vec{u} . \vec{b}) . \vec{b}$

Phương pháp giải:

a) Trên hệ trục Oxy mới, xác định hoành độ, tung độ của vectơ $\vec{u}$

+) $\vec{u} . \vec{a} = | \vec{u} | . | \vec{a} | . \cos (\vec{u} . \vec{a})$

b) Vectơ $\vec{u}$ có tọa độ $(x; y)$ trong hệ trục Oxy với các vectơ đơn vị $\vec{i}; \vec{j}$ thì $\vec{u} = x . \vec{i} + y . \vec{j}$

Lời giải:

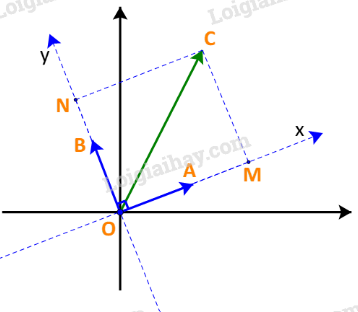
Bài 4.38 trang 72 Toán 10 Tập 1 I Kết nối tri thức (ảnh 3)

a) Trên mặt phẳng tọa độ, lấy các điểm A, B, C sao cho $\vec{O A} = \vec{a}; \vec{O B} = \vec{b}; \vec{O C} = \vec{u}$

Trên hệ trục Oxy với các vectơ đơn vị $\vec{i} = \vec{a}, \vec{j} = \vec{b}$ , lấy M, N là hình chiếu của C trên Ox, Oy.

Gọi tọa độ của $\vec{u}$ là $(x; y)$ . Đặt $α = (\vec{u}, \vec{a})$ .

+) Nếu $0^{o} < α < 90^{o}$ : $x = O M = | \vec{u} | . \cos α = | \vec{u} | . \cos α . | \vec{a} | = \vec{u} . \vec{a};$

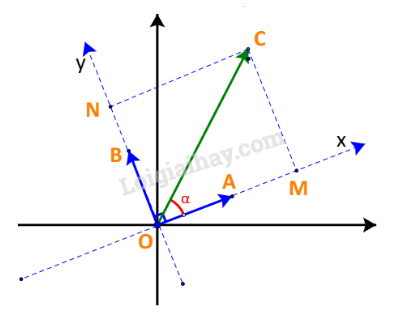
Bài 4.38 trang 72 Toán 10 Tập 1 I Kết nối tri thức (ảnh 2)

+) Nếu $90^{o} < α < 180^{o}$ : $x = - O M = - | \vec{u} | . \cos (180^{o} - α) = | \vec{u} | . \cos α = \vec{u} . \vec{a};$

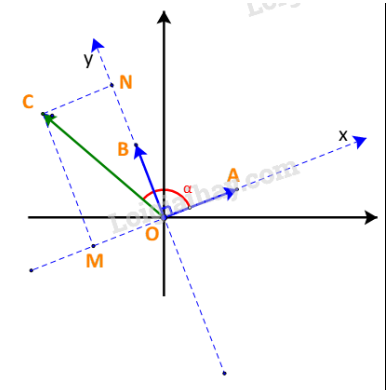
Bài 4.38 trang 72 Toán 10 Tập 1 I Kết nối tri thức (ảnh 1)

Như vậy ta luôn có: $x = \vec{u} . \vec{a}$

Chứng minh tương tự, ta có: $y = \vec{u} . \vec{b}$

Vậy vectơ $\vec{u}$ có tọa độ là $(\vec{u} . \vec{a}; \vec{u} . \vec{b})$

b) Trong hệ trục Oxy với các vectơ vectơ đơn vị $\vec{i} = \vec{a}, \vec{j} = \vec{b}$ , vectơ $\vec{u}$ có tọa độ là $(\vec{u} . \vec{a}; \vec{u} . \vec{b})$

$\begin{array}{l} \Rightarrow \vec{u} = (\vec{u} . \vec{a}) . \vec{i} + (\vec{u} . \vec{b}) . \vec{j} \\ \Leftrightarrow \vec{u} = (\vec{u} . \vec{a}) . \vec{a} + (\vec{u} . \vec{b}) . \vec{b} \end{array}$

Bài 4.39 trang 72 Toán 10: Trên sông, một cano chuyển động thẳng đều theo hướng $S 15^{o} E$ với vận tốc có độ lớn bằng 20 km/h. Tính vận tốc riêng của cano, biết rằng, nước trên sông chảy về hướng đông với vận tốc có độ lớn bằng 3 km/h.

Phương pháp giải:

Định lí cosin trong tam giác OAC: $A C^{2} = O A^{2} + O C^{2} - 2. O A . O C . \cos \hat{A O C}$

Lời giải:

Lấy các điểm: A, C sao cho:

Vectơ vận tốc dòng nước $\vec{v_{n}} = \vec{O A}$

Vectơ vận tốc chuyển động $\vec{v_{c a n o}} = \vec{O C}$

Ta có: $\vec{v_{c a n o}} = \vec{v_{n}} + \vec{v}$ , với $\vec{v}$ là vectơ vận tốc riêng của cano.

Gọi B là điểm sao cho $\vec{v} = \vec{O B}$ thì OACB là hình bình hành.

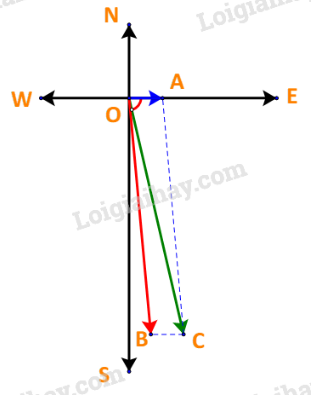
Bài 4.39 trang 72 Toán 10 Tập 1 I Kết nối tri thức (ảnh 1)

Vì tàu chuyển động theo hướng $S 15^{o} E$ nên vectơ $\vec{O C}$ tạo với hướng Nam (tia OS) góc $15^{o}$ và tạo với hướng Đông (tia OE) góc $90^{o} - 15^{o} = 75^{o}$ .

Mà nước trên sông chảy về hướng đông nên vectơ $\vec{O A}$ cùng hướng với vectơ $\vec{O E}$

Do đó góc tạo bởi vectơ $\vec{O C}$ và vectơ $\vec{O A}$ là $75^{o}$

Xét tam giác OAC ta có:

$O A = | \vec{v_{n}} | = 3$ ; $O C = | \vec{v_{c a n o}} | = 20$ và $\hat{A O C} = 75^{o}$

Áp dụng định lí cosin tại đỉnh O ta được:

$\begin{array}{l} A C^{2} = O A^{2} + O C^{2} - 2. O A . O C . \cos \hat{A O C} \\ \Leftrightarrow A C^{2} = 3^{2} + 20^{2} - 2.3.20. \cos 75^{o} \approx 378 \\ \Leftrightarrow O B = A C \approx 19, 44 \end{array}$