Với giải Câu hỏi trang 51 Toán 10 Tập 1 Cánh Diều trong Bài 4: Bất phương trình bậc nhất hai ẩn học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Nội dung bài viết
Toán 10 Cánh Diều trang 51 Bài 4: Bất phương trình bậc nhất hai ẩn
Hoạt động 3 trang 51 SGK Toán 10 tập 1: Cho bất phương trình x2−4x+3>0(2).
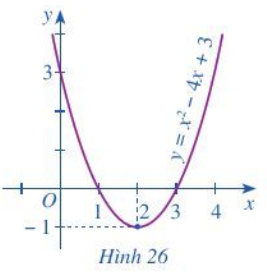
Quan sát parabol (P):x2−4x+3 ở Hình 26 và cho biết:
a) Bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía nào của trục hoành.
b) Phần parabol (P) nằm phía trên trục hoành ứng với những giá trị nào của x.
Phương pháp giải:
- Nếu dấu bất phương trình dương thì bất phương trình biểu diễn phần (P) phía trên trục hoành và ngược lại.
Lời giải:
a) Từ đồ thị ta thấy bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía trên trục hoành.
b) Phần parabol (P) nằm phía trên trục hoành ứng với các giá trị của x thuộc (−∞;1)∪(3;+∞)
a) x2+2x+2>0
b) −3x2+2x−1>0
Phương pháp giải:
Bước 1: Vẽ đồ thị biểu diễn các hàm số.
Bước 2: Quan sát đồ thị và lấy các giá trị tương ứng với bất phương trình.
Lời giải:
a) Ta có đồ thị:
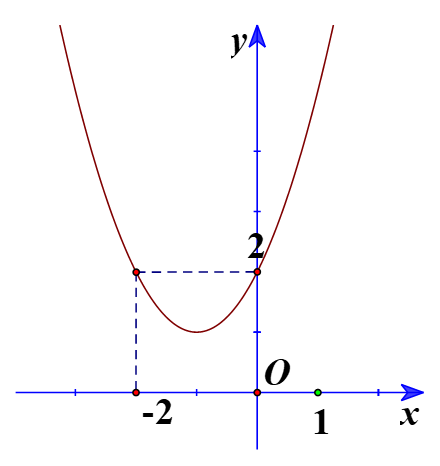
Từ đồ thị ta thấy x2+2x+2>0 biểu diễn phần parabol y=x2+2x+2 nằm phía trên trục hoành, tương ứng với mọi x∈R.
Vậy tập nghiệm của bất phương trình x2+2x+2>0 là R.
b) Ta có đồ thị:
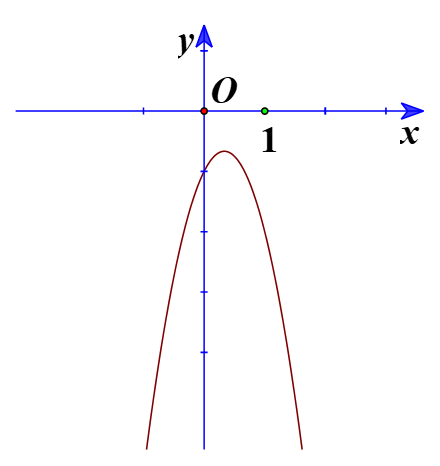
Từ đồ thị ta thấy −3x2+2x−1>0 biểu diễn phần parabol y=−3x2+2x−1 nằm phía trên trục hoành, tương ứng với x∈∅
Vậy tập nghiệm của bất phương trình −3x2+2x−1>0 là ∅.
Xem thêm các lời giải Toán 10 Cánh Diều hay, chi tiết khác:
Luyện tập – vận dụng 2 trang 50 SGK Toán 10 tập 1: Giải các bất phương trình bậc hai sau...
Hoạt động 3 trang 50, 51 SGK Toán 10 tập 1: Cho bất phương trình x2−4x+3>0(2)...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.