Với giải Câu hỏi trang 89 SBT Toán 10 Tập 2 Cánh Diều trong Bài 5: Phương trình đường thẳng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập SBT Toán 10. Mời các bạn đón xem:
SBT Toán 10 Cánh Diều trang 89 Bài 5: Phương trình đường thẳng
A. (x-4)2+(y+2)2=81;
B. (x+4)2+(y-2)2=9;
C. (x-4)2+(y+2)2=9;
D. (x+4)2+(y-2)2=81.
Lời giải:
Đường tròn tâm I(- 4; 2) bán kính R = 9 có phương trình là: (x+4)2+(y-2)2=81
Vậy chọn đáp án D.
Bài 51 trang 89 SBT Toán 10: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 3)2 + (y – 4)2 = 25. Tiếp tuyến tại điểm M(0; 8) thuộc đường tròn có một vectơ pháp tuyến là:
A. =(-3;4);
B. =(3;4);
C. =(4;-3);
D. =(4;3).
Lời giải:
Đường tròn có tâm I(3; 4).
Tiếp tuyến tại M của đường tròn có vectơ pháp tuyến là vectơ =(-3;4)
Vậy chọn đáp án A.
Bài 52 trang 89 SBT Toán 10: Trong mặt phẳng tọa độ Oxy, cho đường tròn (x – 6)2 + (y – 7)2 = 16. Hai điểm M, N chuyển động trên đường tròn (C). Khoảng cách lớn nhất giữa hai điểm M và N bằng:
A. 16;
B. 8;
C. 4;
D. 256.
Lời giải:
Do M, N chuyển động trên đường tròn nên khoảng cách lớn nhất giữa 2 điểm M, N chính bằng đường kính của đường tròn.
Bán kính của đường tròn (C) là: R==4.
Vậy độ dài lớn nhất của MN = 2R = 8. Chọn đáp án B.
Bài 53 trang 89 SBT Toán 10: Tìm k sao cho phương trình: x2 + y2 – 6x + 2ky + 2k + 12 = 0 là phương trình đường tròn.
Lời giải:
Ta biến đổi như sau:
x2 + y2 – 6x + 2ky + 2k + 12 = 0
⇔ (x – 3)2 + (y + k)2 = k2 – 2k – 3
Để phương trình trên là phương trình đường tròn thì
k2 – 2k – 3>0
Vậy k < – 1 hoặc k > 3.
Bài 54 trang 89 SBT Toán 10: Viết phương trình đường tròn (C) trong mỗi trường hợp sau:
a) (C) có tâm I(- 6; 2) bán kính 7.
b) (C) có tâm I(3; - 7) và đi qua điểm A(4; 1)
c) (C) có tâm I(1; 2) và tiếp xúc với đường thẳng 3x + 4y + 19 = 0.
d) (C) có đường kính AB với A(- 2; 3) và B(0; 1)
e) (C) có tâm I thuộc đường thẳng :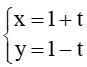
Lời giải:
a) Phương trình (C) có tâm I(- 6; 2) bán kính 7 là: (x + 6)2 + (y – 2)2 = 72.
b) Bán kính của đường tròn (C) là: IA =|| =
Phương trình đường tròn là: (x-3)2+(y+7)2 =65.
c) Bán kính của đường tròn chính bằng khoảng cách từ I đến đường thẳng d: 3x + 4y + 19 = 0.
Suy ra R=d(I,d)= 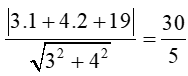
Phương trình đường tròn là: (x -1)2 + (y – 2)2 = 36.
d) Gọi I là tâm của đường tròn thì IA = R và I là trung điểm của AB
Suy ra I(-1; 2), IA =|| =
Phương trình đường tròn là: (x +1)2 + (y – 2)2 = 2.
e) Tâm I thuộc đường thẳng :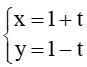
Đường tròn có 2 tiếp tuyến nên khoảng cách từ I đến 2 tiếp tuyến bằng nhau và bằng bán kính của đường tròn.
Ta có: d(I,)=d(I,)
|t-6|=|7t+1|
Với t = thì I và R = d(I; ∆2) = 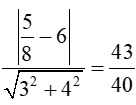
Với t = thì I và R = d(I; ∆2) = 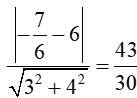
Bài 55 trang 89 SBT Toán 10: Lập phương trình đường thẳng ∆ là tiếp tuyến của đường tròn (C): (x+2)2+(y-3)2=4 trong mỗi trường hợp sau:
a) ∆ tiếp xúc (C) tại điểm có tung độ bằng 3.
b) ∆ vuông góc với đường thẳng 5x – 12y + 1 = 0.
c) ∆ đi qua điểm D(0; 4).
Lời giải:
Đường tròn có tâm I(-2; 3) và bán kính R = 2.
a) Hoành độ của điểm có tung độ bằng 3 là:
(x+2)2+(3-3)2=4
Suy ra ta có 2 điểm M(0; 3) và điểm N(-4; 3).
Vectơ pháp tuyến của đường thẳng IM là: =(2;0).
Phương trình đường thẳng IM: 2(x – 0) = 0 hay x = 0.
Vectơ pháp tuyến của đường thẳng IN là: =(-2;0).
Phương trình đường thẳng IN: - 2(x + 4) = 0 hay x + 4 = 0.
Vậy phương trình đường thẳng là: x = 0 hoặc x + 4 = 0.
b) ∆ vuông góc với đường thẳng 5x – 12y + 1 = 0
nên ∆ có dạng: 12x + 5y + c = 0.
Khoảng cách từ I đến ∆ bằng R nên d(I,∆)=2
Với c = 35 thì phương trình tiếp tuyến là: 12x + 5y + 35 =0
Với c = - 17 thì phương trình tiếp tuyến là: 12x + 5y – 17 =0
c) Gọi H(a ;b) là tiếp điểm.
Do D(0; 4) thuộc nên DH vuông góc với IH và IH = R = 2.
Ta có: =(a;b-4) và =(a+2;b-3)
⇒ IH = ||==2
⇔ a2 + 4a + 4 + b2 – 6b + 9 = 4
⇔ a2 + 4a + b2 – 6b + 9 = 0 (1)
Ta lại có: .=0 a(a+2)+(b-4)(b-3)=0
⇔ a2 + 2a + b2 – 7b + 12 = 0 (2)
Từ (1) và (2) ta có hệ phương trình:
Với a = 0, b = 3 thì H(0; 3)
Suy ra =(2;0)
Do đó phương trình tiếp tuyến cần tìm là: 2(x – 0) = 0 ⇔ x = 0.
Với a=; b=
Suy ra =
Do đó phương trình tiếp tuyến cần tìm là: 3(x – 0) + 4(y – 4) = 0 ⇔ 3x + 4y – 16 = 0.
Vậy có hai đường thẳng ∆ thỏa mãn yêu cầu là x = 0 hoặc 3x + 4y – 16 = 0.
Bài 56 trang 89 SBT Toán 10: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x+2)2+(y-4)2=25 và điểm A(- 1; 3)
a) Xác định vị trí tương đối của điểm A đối với đường tròn (C).
b) Đường thẳng d thay đổi đi qua A cắt đường tròn tại M và N. Viết phương trình đường thẳng d sao cho MN ngắn nhất.
Lời giải:
a) Đường tròn (C) có tâm I(-2; 4) và bán kính R = = 5.
Ta có: IA=||= < 5
Do đó A nằm trong đường tròn (C).
b) Dây cung MN ngắn nhất khi khoảng cách từ tâm I đến dây cung là lớn nhất
Do d đi qua A cố định nên khi d thay đổi thì khoảng cách lớn nhất từ I đến d chính bằng IA.
Hay IA vuông góc với d.
Vectơ pháp tuyến của đường thẳng d: =(1;-1)
Phương trình đường thẳng d: (x + 1) – (y – 3) = 0 ⇔ x – y + 4 = 0.
Xem thêm các bài giải sách bài tập Toán lớp 10 Cánh Diều hay, chi tiết khác:
Bài 47 trang 88 SBT Toán 10: Phương trình nào sau đây không là phương trình đường tròn?...
Bài 52 trang 89 SBT Toán 10: Trong mặt phẳng tọa độ Oxy, cho đường tròn (x – 6)2 + (y – 7)2 = 16...
Bài 53 trang 89 SBT Toán 10: Tìm k sao cho phương trình: x2 + y2 – 6x + 2ky + 2k + 12 = 0...
Bài 54 trang 89 SBT Toán 10: Viết phương trình đường tròn (C) trong mỗi trường hợp sau: a) (C) có tâm I(- 6; 2) bán kính 7...
Bài 56 trang 89 SBT Toán 10: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x+2)2+(y-4)2=25...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.