Sau bài học này ta giải quyết được bài toán như sau:

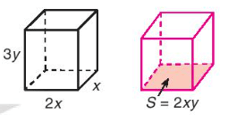
Thể tích của khối hộp thứ nhất là: 2x . x . 3y = 6x²y.

Vì hai khối hộp có cùng thể tích nên khối hộp thứ hai có thể tích 6x²y.

Chiều cao của khối hộp thứ hai là: 6x²y : 2xy = 3x.

Vậy chiều cao (cạnh bên) của khối hộp thứ hai là 3x.

HĐ1 trang 22 Toán 8 Tập 1: Hãy nhớ lại cách chia đơn thức cho đơn thức trong trường hợp chúng có cùng một biến và hoàn thành các yêu cầu sau:

a) Thực hiện phép chia 6x³ : 3x².

b) Với a, b ∈ ℝ và b ≠ 0; m, n ∈ ℕ, hãy cho biết:

• Khi nào thì ax^m chia hết cho bxⁿ.

• Nhắc lại cách thực hiện phép chia ax^m cho bxⁿ.

Lời giải:

a) Ta có 6x³ : 3x² = (6: 3)(x³ : x²) = 2x.

b) Với a, b ∈ ℝ và b ≠ 0; m, n ∈ ℕ, ta có:

• ax^m chia hết cho bxⁿ khi m ≥ n.

• Thực hiện phép chia: ax^m : bxⁿ = (a : b) . (x^m : xⁿ) = $\frac{a}{b}{x}^{m-n}$ .

HĐ2 trang 22 Toán 8 Tập 1: Với mỗi trường hợp sau, hãy đoán xem đơn thức A có chia hết cho đơn thức B không; nếu chia hết, hãy tìm thương của phép chia A cho B và giải thích cách làm:

a) A = 6x³y, B = 3x²y;

b) A = x²y, B = xy².

Lời giải:

a) Dự đoán: Đơn thức A chia hết cho đơn thức B.

Ta có: A : B = 6x³y : 3x²y = (6 : 3)(x³ : x²)(y : y)

= 2 . x . 1 = 2x.

b) Dự đoán: Đơn thức A không chia hết cho đơn thức B.

A : B = (x² : x)(y : y²) (đơn thức A không chia hết cho đơn thức B)

Giải Toán 8 trang 23 Tập 1

Luyện tập 1 trang 23 Toán 8 Tập 1: Trong các phép chia sau đây, phép chia nào không là phép chia hết? Tại sao?

Tìm thương của các phép chia còn lại:

a) −15x²y² chia cho 3x²y;

b) 6xy chia cho 2yz;

c) 4xy³ chia cho 6xy².

Lời giải:

Phép chia 6xy chia cho 2yz không là phép chia hết vì số mũ của biến z trong đơn thức 6xy nhỏ hơn số mũ của biến z trong đơn thức 2yz.

a) Ta có: −15x²y² : 3x²y = (−15 : 3)(x² : x²)(y² : y) = −5y.

Vậy thương của −15x²y² chia cho 3x²y là −5y.

c) Ta có: $4x{y}^3:6x{y}^2=\left(4:6\right)\left(x:x\right)\left(y^3:y^2\right)$$=\frac{2}{3}y$

Vậy thương của 4xy³ chia cho 6xy² là $\frac{2}{3}y$.

Vận dụng 1 trang 23 Toán 8 Tập 1: Giải bài toán mở đầu.

Cho hai khối hộp chữ nhật: khối hộp thứ nhất có ba kích thước x, 2x và 3y; khối hộp thứ hai có diện tích đáy là 2xy. Tính chiều cao (cạnh bên) của khối hộp thứ hai, biết rằng hai khối hộp có cùng thể tích.

Lời giải:

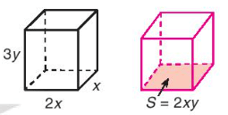
Thể tích của khối hộp thứ nhất là: 2x . x . 3y = 6x²y.

Vì hai khối hộp có cùng thể tích nên khối hộp thứ hai có thể tích 6x²y.

Chiều cao của khối hộp thứ hai là: 6x²y : 2xy = 3x.

Vậy chiều cao (cạnh bên) của khối hộp thứ hai là 3x.

Giải Toán 8 trang 24 Tập 1

Luyện tập 2 trang 24 Toán 8 Tập 1: Làm tính chia (6x⁴y³ – 8x³y⁴ + 3x²y²) : 2xy².

Lời giải:

Ta có (6x⁴y³ – 8x³y⁴ + 3x²y²) : 2xy²

= 6x⁴y³ : 2xy² – 8x³y⁴ : 2xy² + 3x²y² : 2xy²

= 3x³y – 4x²y² + $\frac{3}{2}x$ .

Vận dụng 2 trang 24 Toán 8 Tập 1: Tìm đa thức A sao cho A . (−3xy) = 9x³y + 3xy³ – 6x²y².

Lời giải:

Ta có A . (−3xy) = 9x³y + 3xy³ – 6x²y².

Suy ra A = (9x³y + 3xy³ – 6x²y²) : (−3xy)

= 9x³y : (−3xy) + 3xy³ : (−3xy) – 6x²y² : (−3xy)

= −3x²y − y² + 2xy.

Bài 1.30 trang 24 Toán 8 Tập 1: a) Tìm đa thức M, biết rằng $\frac{7}{3}{x}^3{y}^2:M=7x{y}^2$ .

b) Tìm đa thức N sao cho N : 0,5xy²z = −xy.

Lời giải:

a) Ta có $\frac{7}{3}{x}^3{y}^2:M=7x{y}^2$

Suy ra $M=\frac{7}{3}{x}^3{y}^2:7x{y}^2=\left(\frac{7}{3}:7\right)\left(x^3:x\right)\left(y^2:y^2\right)$ .

Vậy $M=\frac{1}{3}{x}^2$.

b) Ta có N : 0,5xy²z = −xy

Suy ra N = −xy . 0,5xy²z = −0,5(x . x)(y . y²)z = −0,5x²y³z.

Vậy N = −0,5x²y³z.

Bài 1.31 trang 24 Toán 8 Tập 1: Cho đa thức A = 9xy⁴ – 12x²y³ + 6x³y². Với mỗi trường hợp sau đây, xét xem A có chia hết cho đơn thức B hay không? Thực hiện phép chia trong trường hợp A chia hết cho B.

a) B = 3x²y;

b) B = −3xy².

Lời giải:

a) Đa thức A = 9xy⁴ – 12x²y³ + 6x³y² không chia hết cho đơn thức B = 3x²y vì đơn thức 9xy⁴ không chia hết cho 3x²y.

Do đó, đa thức A = 9xy⁴ – 12x²y³ + 6x³y² không chia hết cho đơn thức B = 3x²y.

b) Đa thức A = 9xy⁴ – 12x²y³ + 6x³y² chia hết cho đơn thức B = −3xy².

Ta có: A : B = 9xy⁴ : (−3xy²) – 12x²y³ : (−3xy²) + 6x³y² : (−3xy²)

= −3xy² + 4xy − 2x².

Bài 1.32 trang 24 Toán 8 Tập 1: Thực hiên phép chia (7y⁵z² – 14y⁴z³ + 2,1y³z⁴) : (−7y³z²).

Lời giải:

Ta có (7y⁵z² – 14y⁴z³ + 2,1y³z⁴) : (−7y³z²)

= 7y⁵z² : (−7y³z²) – 14y⁴z³ : (−7y³z²) + 2,1y³z⁴ : (−7y³z²)

= −y² + 2yz – 0,3z².

Xem thêm các bài giải Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 4: Phép nhân đa thức

Luyện tập chung trang 25

Bài tập cuối chương 1