Giải Toán 11 trang 32 Tập 1 (Cánh Diều)

Ngọc Nguyễn Ngày: 06-02-2024 Lớp 11

349

Với giải SGK Toán 11 Cánh Diều trang 32 chi tiết trong Bài 4: Phương trình lượng giác cơ bản giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 trang 32 Tập 1 (Cánh Diều)

Câu hỏi khởi động trang 32 Toán 11 Tập 1: Một vệ tinh nhân tạo bay quanh Trái Đất theo một quỹ đạo là đường elip (Hình 32). Độ cao h (km) của vệ tinh so với bề mặt Trái Đất được xác định bởi công thức h = 550 + 450cos $\frac{π}{50}$ t (Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2021), trong đó t là thời gian tính bằng phút kể từ lúc vệ tinh bay vào quỹ đạo. Tại thời điểm t bằng bao nhiêu thì vệ tinh cách mặt đất 1 000 km; 250 km; 100 km?

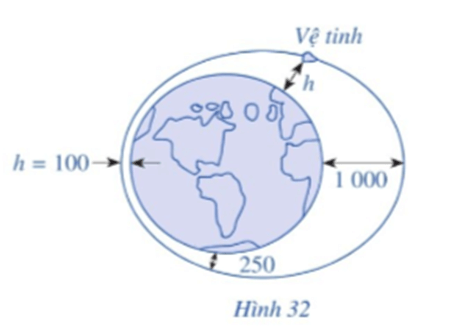
Toán 11 Bài 4 (Cánh diều): Phương trình lượng giác cơ bản (ảnh 1)

Trên thực tế, có nhiều bài toán dẫn đến việc giải một trong các phương trình có dạng: sinx = m, cosx = m, tanx = m, cotx = m, trong đó x là ẩn số, m là số thực cho trước. Các phương trình đó là các phương trình lượng giác cơ bản.

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

• Để vệ tinh cách mặt đất 1 000 km thì 550 + 450cos $\frac{π}{50}$ t = 1 000

$\Leftrightarrow$ 450cos $\frac{π}{50}$ t=450

$\Leftrightarrow$ cos $\frac{π}{50}$ t = 1

$\Leftrightarrow$ $\frac{π}{50}$ t = k2 $π$ (k $\in Z$ , t $\geq$ 0)

$\Leftrightarrow$ t = k2 $π$ . $\frac{50}{π}$ = 100k (k $\in Z$ {0; 1; 2; 3;...}

Vậy tại các thời điểm t = 100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 1 000 km.

• Để vệ tinh cách mặt đất 250 km thì 550 + 450cos $\frac{π}{50}$ t = 250

$\Leftrightarrow$ 450cos $\frac{π}{50}$ t = -300

$\Leftrightarrow$ cos $\frac{π}{50}$ t = - $\frac{2}{3}$

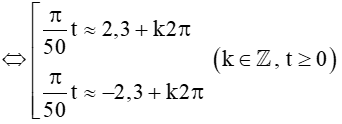
Toán 11 Bài 4 (Cánh diều): Phương trình lượng giác cơ bản (ảnh 2)

(Dùng máy tính cầm tay (chuyển về chế độ “radian”) bấm liên tiếp Toán 11 Bài 4 (Cánh diều): Phương trình lượng giác cơ bản (ảnh 3) ta được kết quả gần đúng là 2,3)

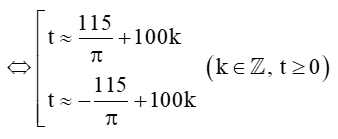
Toán 11 Bài 4 (Cánh diều): Phương trình lượng giác cơ bản (ảnh 4)

Vậy tại các thời điểm t $\approx \pm \frac{115}{π}$ +100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 250 km.

• Để vệ tinh cách mặt đất 100 km thì 550 + 450cos $\frac{π}{50}$ t = 100

$\Leftrightarrow$ 450cos $\frac{π}{50}$ t = -450

$\Leftrightarrow$ cos $\frac{π}{50}$ t = -1

$\Leftrightarrow$ $\frac{π}{50}$ t = $π$ +k2 $π$ (k $\in$ Z, t $\geq$ 0).

$\Leftrightarrow$ t = 50+100k (k $\in$ {0;1;2;3;...}

Vậy tại các thời điểm t = 50 + 100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 100 km.

I. Phương trình tương đương

Hoạt động 1 trang 32 Toán 11 Tập 1: Cho hai phương trình (với cùng ẩn x):

x² ‒ 3x + 2 = 0 (1)

(x – 1)(x – 2) = 0 (2)

a) Tìm tập nghiệm S₁ của phương trình (1) và tập nghiệm S₂ của phương trình (2).

b) Hai tập S₁, S₂ có bằng nhau hay không?

Lời giải:

a) Ta có:

x² ‒ 3x + 2 = 0 (1)

Suy ra x = 1 hoặc x = 2.

Vậy phương trình (1) có tập nghiệm S₁ = {1; 2}.

(x – 1)(x – 2) = 0 (2)

Suy ra x = 1 hoặc x = 2.

Vậy phương trình (2) có tập nghiệm S₂ = {1; 2}.

b) Hai tập S₁, S₂ bằng nhau vì cùng là tập {1; 2}.

Luyện tập 1 trang 32 Toán 11 Tập 1: Hai phương trình x – 1 = 0 và $\frac{x^{2} - 1}{x + 1}$ =0 có tương đương không? Vì sao?

Lời giải:

Tập nghiệm của phương trình x – 1 = 0 là S₁ = {1}.

Tập nghiệm của phương trình $\frac{x^{2} - 1}{x + 1}$ là S₂ = {1}.

Vì S₁ = S₂ nên hai phương trình x – 1 = 0 và $\frac{x^{2} - 1}{x + 1}$ =0 tương đương.

Từ khóa :

Giải bài tập Toán 11

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

291

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

312

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

340

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

288