Toptailieu biên soạn và giới thiệu lời giải Toán 8 Bài 6 (Cánh diều): Hình thoi hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 8 Bài 6 từ đó học tốt môn Toán 8.
Toán 8 (Cánh diều) Bài 6: Hình thoi
Khởi động trang 113 Toán 8 Tập 1: Hoạ tiết trên vải ở Hình 55 gợi lên hình ảnh của hình thoi.

Hình thoi có những tính chất gì? Có những dấu hiệu nào để nhận biết một tứ giác là hình thoi?
Lời giải:
Sau bài học này chúng ta sẽ giải quyết câu hỏi trên như sau:
‒ Trong một hình thoi:
+ Bốn cạnh bằng nhau;
+ Các cạnh đối song song.
+ Các góc đối bằng nhau.
+ Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
+ Hai đường chéo là các đường phân giác của các góc ở đỉnh.
‒ Dấu hiệu nhận biết hình thoi:
+ Hình bình hành có hai cạnh kề nhau là hình thoi.
+ Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
+ Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
I. Định nghĩa
Hoạt động 1 trang 113 Toán 8 Tập 1: So sánh độ dài các cạnh của tứ giác ABCD ở Hình 56.
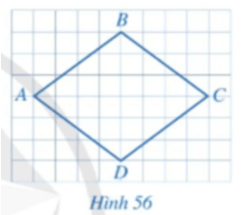
Lời giải:
Xét tứ giác ABCD ở Hình 56 ta có: AB = BC = CD = DA.
II. Tính chất
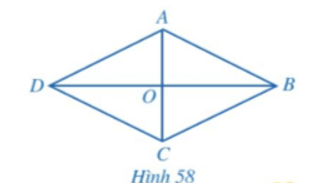
a) Hình thoi ABCD có là hình bình hành hay không?
b) Hai đường chéo AC và BD có vuông góc với nhau hay không?
c) Hai tam giác ABC và ADC có bằng nhau hay không? Tia AC có phải là tia phân giác của hay không?
Lời giải:
a) Do ABCD là hình thoi nên AB = BC = CD = DA.
Xét tứ giác ABCD có: AB = CD, AD = BC nên ABCD là hình bình hành.
b) Do ABCD là hình bình hành nên OB = OD.
Xét ΔOAD và ΔOAB có:
OA là cạnh chung;
AD = AB (chứng minh trên);
OD = OB (chứng minh trên).
Do đó ΔOAD = ΔOAB (c.c.c)
Suy ra (hai góc tương ứng)
Mà . (hai góc kề bù)
Do đó hay AC ⊥ BD tại O.
c) Xét ΔABC và ΔADC có:
AC là cạnh chung;
AB = AD (chứng minh câu a);
BC = DC (chứng minh câu a)
Do đó ΔABC = ΔADC (c.c.c)
Suy ra (hai góc tương ứng)
Nên AC là tia phân giác của .
Luyện tập 1 trang 114 Toán 8 Tập 1: Cho hình thoi ABCD có . Chứng minh tam giác ABD là tam giác đều.
Lời giải:
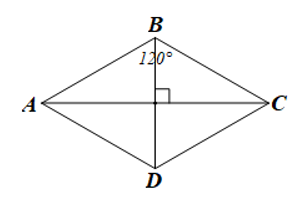
Do ABCD là hình thoi nên AB = AD
Tam giác ABD có AB = AD nên là tam giác cân tại A.
Do ABCD là hình thoi nên BD là tia phân giác của góc ABC.
Suy ra .
Xét ΔABD cân có nên là tam giác đều.
III. Dấu hiệu nhận biết
b) Cho hình bình hành ABCD có hai đường chéo AC và BD vuông góc với nhau (Hình 60).
• Đường thẳng AC có phải là đường trung trực của đoạn thẳng BD hay không?
• ABCD có phải là hình thoi hay không?
Lời giải:
a) Do ABCD là hình bình hành nên AB = CD và AD = BC.
Mà AB = BC nên AB = BC = CD = DA.
Tứ giác ABCD có bốn cạnh bằng nhau nên là hình thoi.
b) • Do ABCD là hình bình hành nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường
Do đó AC ⊥ BD tại trung điểm O của đoạn thẳng BD.
Suy ra AC là đường trung trực của đoạn thẳng BD.
• Vì AC là đường trung trực của đoạn thẳng BD nên AD = AB.
Theo kết quả câu a, hình bình hành ABCD có hai cạnh kề AD và AB bằng nhau nên là hình thoi.
Lời giải:
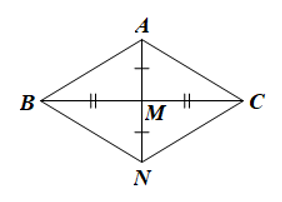
Do MN = MA nên M là trung điểm của AN.
Xét tứ giác ABNC có hai đường chéo AN và BC cắt nhau tại trung điểm M của mỗi đường
Do đó ABNC là hình bình hành.
Mặt khác, ΔABC cân tại A có AM là đường trung tuyến đồng thời là đường cao
Do đó AM ⊥ BC hay AN ⊥ BC.
Suy ra hình bình hành ABNC có hai đường chéo vuông góc với nhau nên là hình thoi.
Bài tập
Lời giải:
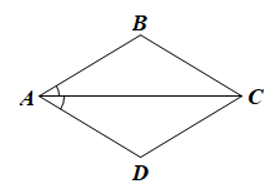
Do AC là tia phân giác của góc DAB nên .
Mặt khác do ABCD là hình bình hành nên AB // CD
Suy ra (so le trong).
Do đó
Xét ΔDAC có nên ΔDAC cân tại D .
Suy ra DA = DC.
Hình bình hành ABCD có hai cạnh kề DA và DC bằng nhau nên là hình thoi.
AC2 + BD2 = 4(OA2 + OB2) = 4AB2.
Lời giải:
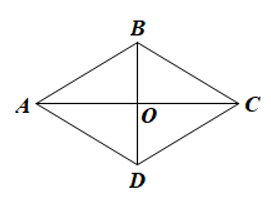
Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường.
Do đó AC = 2OA, BD = 2OB.
Ta có: AC2 + BD2 = (2OA)2 + (2OB)2 = 4OA2 + 4OB2 = 4(OA2 + OB2).
Xét ΔOAB vuông tại O, theo định lí Pythagore ta có:
AB2 = OA2 + OB2
Suy ra AC2 + BD2 = 4(OA2 + OB2) = 4AB2.
Bài 3 trang 115 Toán 8 Tập 1: Cho hình thoi ABCD có . Tính số đo mỗi góc của hình thoi ABCD.
Lời giải:
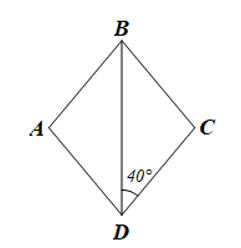
Vì ABCD là hình thoi nên BD là phân giác của
Do đó .
Suy ra .
Do ABCD là hình thoi nên AB // CD, do đó
Suy ra .
Do đó .
Vậy và .
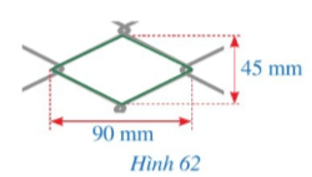
Lời giải:
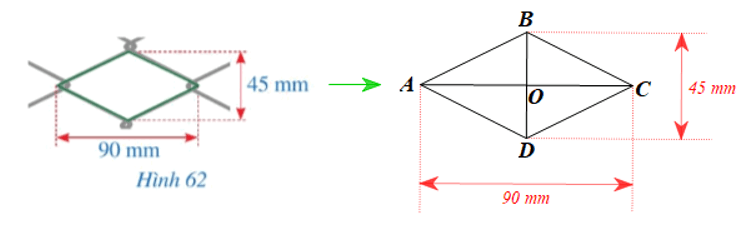
Giả sử một lưới mắt cáo được mô tả bởi hình thoi ABCD như hình vẽ trên.
Khi đó AC = 90 mm, BD = 45 mm.
Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường.
Suy ra ; .
Xét ΔOAB vuông tại O, theo định lí Pythagore ta có:
AB2 = OA2 + OB2 = 452 + 22,52 = 2 025 + 506,25 = 2531,25
Suy ra .
Lời giải:
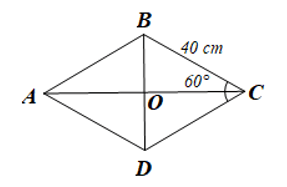
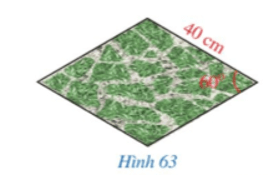
Giả sử viên gạch trang trí được mô tả bởi hình thoi ABCD như hình vẽ trên với
• Tam giác BCD có BC = CD (do ABCD là hình thoi) nên là tam giác cân tại C.
Lại có nên ΔBCD là tam giác đều.
Do đó BC = CD = BD = 40 cm.
• Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường.
Suy ra .
Xét ΔOBC vuông tại O, theo định lí Pythagore ta có:
BC2 = OB2 + OC2
Do đó OC2 = BC2 – OB2 = 402 – 202 = 1 600 – 400 = 1 200.
Suy ra
Mà O là trung điểm của AC nên AC = 2OC ≈ 69,28 (cm).
• Diện tích của viên gạch có dạng hình thoi đó là
.
Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.