Toptailieu biên soạn và giới thiệu lời Giải Toán 8 Bài 9: Phân tích đa thức thành nhân tử hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi sgk Toán 8 Bài 9 từ đó học tốt môn Toán 8.
Nội dung bài viết
Toán 8 (Kết nối tri thức) Bài 9: Phân tích đa thức thành nhân tử
1. Phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung
HĐ 1 trang 42 Toán 8 Tập 1: Hãy viết đa thức x2−2xy thành tích của các đa thức, khác đa thức là số.
Lời giải:
x2−2xy=x.x−2xy=x(x−2y)
Luyện tập 1 trang 42 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:
a) 6y3+2y
b) 4(x−y)−3x(x−y)
Lời giải:
a) 6y3+2y=2y.(3y2+1)
b) 4(x−y)−3x(x−y)=(x−y)(4−3x)
Vận dụng 1 trang 42 Toán 8 Tập 1: Giải bài toán mở đâu bằng cách phân tích 2x2+x thành nhân tử.
Lời giải:
2x2+x=0⇔x(2x+1)=0⇔[x=02x+1=0⇔[x=0x=−12
Vậy x=0;x=−12
2. Phân tích đa thức thành nhân tử bằng cách sử dụng hằng đẳng thức
Luyện tập 2 trang 43 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử
Lời giải:
a) (x+1)2−y2=(x+1+y)(x+1−y)
b) x3+3x2+3x+1=(x+1)3
c) 8x3−12x2+6x−1=(2x)3−3.(2x)2.1+3.2x.1−13=(2x−1)3
3. Phân tích đa thức thành nhân tử bằng cách nhóm các hạng tử
Luyện tập 3 trang 44 Toán 8 Tập 1: Phân tích đa thức 2x2−4xy+2y−x thành nhân tử.
Lời giải:
2x2−4xy+2y−x=(2x2−4xy)+(2y−x)=2x(x−2y)−(x−2y)=(x−2y)(2x−1)
Vận dụng 2 trang 44 Toán 8 Tập 1: Tính nhanh giá trị của biểu thức
A=x2+2y−2x−xy tại x=2022,y=2020
Lời giải:
A=x2+2y−2x−xy=(x2+2y)−(2x+xy)=x(x+2)−x(2+y)=x[x+2−(2+y)]=x.(x−y)
Thay x=2022,y=2020 vào A ta được:
A=2022.(2022−2020)=2022.2=4044
Tranh luận trang 44 Toán 8 Tập 1: Phân tích đa thức x3−x thành nhân tử.
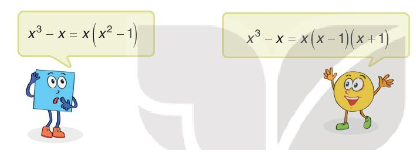
Em hãy nêu ý kiến của em về lời giải của Tròn và Vuông.
Lời giải:
x3−x=x(x2−1)=x(x−1)(x+1)
Bạn Tròn có kết quả đúng, bạn Vuông chưa phân tích triệt để.
Bài tập
Bài 2.22 trang 44 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:
a)x2+xy;b)6a2b−18ab;c)x3−4x;d)x4−8x.
Lời giải:
a)x2+xy=x.x+x.y=x(x+y);b)6a2b−18ab=6ab(a−3);c)x3−4x=x(x2−4)=x(x−2)(x+2);d)x4−8x=x(x3−8)=x(x−2)(x2+2x+4).
Bài 2.23 trang 44 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:
Lời giải:
a)
x2−9+xy+3y=(x2−9)+(xy+3y)=(x−3)(x+3)+y(x+3)=(x+3)(x−3+y)
b)
x2y+x2+xy−1=(x2y+xy)+(x2−1)=xy(x+1)+(x+1)(x−1)=(x+1)(xy+x−1)
Bài 2.24 trang 44 Toán 8 Tập 1: Tìm x biết:
a) x2−4x=0
b) 2x3−2x=0
Lời giải:
a)
x2−4x=0⇔x(x−4)=0⇔[x=0x−4=0⇔[x=0x=4
Vậy x∈{0;4}
b)
2x3−2x=0⇔2x(x2−1)=0⇔2x(x−1)(x+1)=0⇔[x=0x−1=0x+1=0⇔[x=0x=1x=−1
Vậy x∈{0;1;−1}
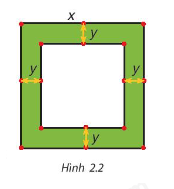
a) Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y.
b) Phân tích S thành nhân tử rồi tính A khi x=102 m, y=2 m.
Lời giải:
a) S=x2−(x−2y)2
b)
S=x2−(x−2y)2=(x−x+2y)(x+x−2y)=2y.(2x−2y)=2y.2(x−y)=4y(x−y)
Khi x=102 m, y=2 m thì S=4.2.(102−2)=800 (m2)
Xem thêm các bài giải Toán 8 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.