Với giải Bài 10 trang 121 Toán 11 Tập 1 Cánh Diều chi tiết trong Bài tập cuối chương 4 giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Bài 10 trang 121 Toán 11 Tập 1 | Cánh Diều Giải Toán lớp 11
Bài 10 trang 121 Toán 11 Tập 1: Một khối gỗ có các mặt đều là một phần của mặt phẳng với (ABCD) // (EFMH), CK // DH. Khối gỗ bị hỏng một góc (Hình 91). Bác thợ mộc muốn làm đẹp khối gỗ bằng cách cắt khối gỗ theo mặt phẳng (R) đi qua K và song song với mặt phẳng (ABCD).
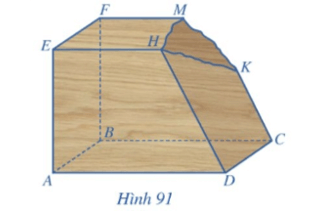
a) Hãy giúp bác thợ mộc xác định giao tuyến của mặt phẳng (R) với các mặt của khối gỗ để cắt được chính xác.
b) Gọi I, J lần lượt là giao điểm DH, BF với mặt phẳng (R). Biết BF = 60 cm, DH = 75 cm, CK = 40 cm. Tính FJ.
Lời giải:
a)
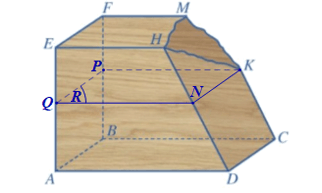
Trong mp(CDHK), qua K vẽ đường thẳng song song với CD, cắt DH tại N.
Trong mp(BCKF), qua K vẽ đường thẳng song song với BC, cắt BF tại P.
Ta có: NK // CD, mà CD ⊂ (ACBD) nên NK // (ABCD).
KP // BC, mà BC ⊂ (ACBD) nên KP // (ABCD).
NK, KP cắt nhau tại K trong mp(NPK).
Do đó (NPK) // (ABCD).
Khi đó mp(R) qua K và song song với (ABCD) chính là mp(NPK).
Trong mp(ADHE), qua N vẽ đường thẳng song song với AD, cắt AE tại Q.
Khi đó mp(R) là mp(NKPQ).
Vậy: (NKPQ) ∩ (ADHE) = QN;
(NKPQ) ∩ (CDHK) = NK;
(NKPQ) ∩ (BCKF) = KP;
(NKPQ) ∩ (ABFE) = PQ.
b)
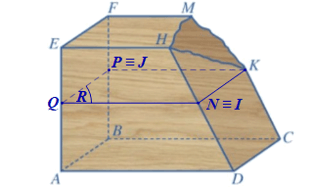
Ta có: DH cắt NK tại N, mà NK ⊂ (R) nên giao điểm của DH và (R) là điểm N.
Theo bài, I là giao điểm của DH và (R) nên điểm I và điểm N trùng nhau.
Tương tự ta cũng có điểm J trùng với điểm P.
Ta có: (ABCD) // (EFMH) và (R) // (ABCD) nên (EFMH) // (R) // (ABCD).
Lại có, hai cát tuyến FB, HD cắt ba mặt phẳng song song (EFMH), (R), (ABCD) lần lượt tại F, J, B và H, I, D nên theo định lí Thalès ta có: .
Mặt khác, trong mp(CDKH), tứ giác CDIK có CK // DI (do CK // DH) và IK // CD
Do đó CDIK là hình bình hành, suy ra DI = CK = 40 cm.
Khi đó HI = DH – DI = 75 – 40 = 35 (cm).
Vì vậy, từ ta có: , suy ra (cm).
Vậy FJ = 28 cm.
Bài 1 trang 120 Toán 11 Tập 1: Trong không gian, hai đường thẳng song song với nhau khi và chỉ khi:
Bài 3 trang 120 Toán 11 Tập 1: Trong không gian, đường thẳng song song với mặt phẳng khi và chỉ khi:
Bài 4 trang 120 Toán 11 Tập 1: Trong không gian, hai mặt phẳng song song với nhau khi và chỉ khi:
Xem thêm các bài giải sách giáo khoa Toán 11 Cánh Dều hay, chi tiết khác:
Bài 2: Hai đường thẳng song song trong không gian
Bài 3: Đường thẳng và mặt phẳng song song
Bài 4: Hai mặt phẳng song song
Bài 5: Hình lăng trụ và hình hộp
Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.