Với giải Bài 7 trang 121 Toán 11 Tập 1 Cánh Diều chi tiết trong Bài tập cuối chương 4 giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Bài 7 trang 121 Toán 11 Tập 1 | Cánh Diều Giải Toán lớp 11
Bài 7 trang 121 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD) và AB = 2CD. Gọi M, N lần lượt là trung điểm các cạnh SA, SB. Chứng minh rằng:
a) MN // (SCD);
b) DM // (SBC);
c) Lấy điểm I thuộc cạnh SD sao cho . Chứng minh rằng: SB // (AIC).
Lời giải:
a)
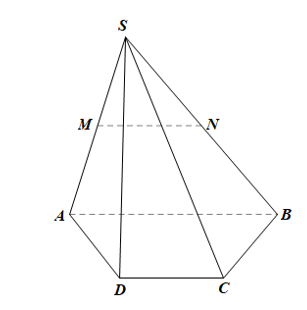
Trong mp(SAB), xét DSAB có M, N lần lượt là trung điểm của SA, SB nên MN là đường trung bình của tam giác
Do đó MN // AB.
Mà AB // CD (giả thiết) nên MN // CD.
Lại có CD ⊂ (SCD) nên MN // (SCD).
b)
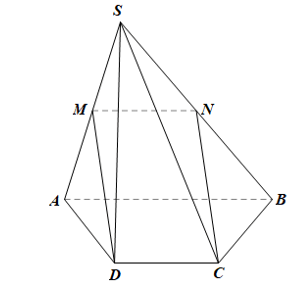
Theo câu a, MN là đường trung bình của SAB nên MN = AB
Mà AB = 2CD hay CD = AB
Do đó MN = CD.
Xét tứ giác MNCD có: MN // CD và MN = CD nên MNCD là hình bình hành
Suy ra DM // CN
Mà CN ⊂ (SBC) nên DM // (SBC).
c)
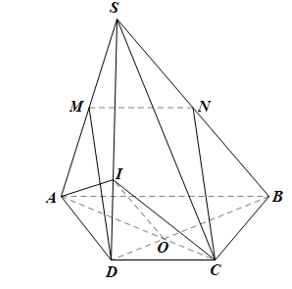
• Trong mp(ABCD), gọi O là giao điểm của AC và BD.
Do AB // CD, theo hệ quả định lí Thalès ta có:
Suy ra hay
• Trong mp(SDB), xét SDB có nên IO // SB (theo định lí Thalès đảo)
Mà IO ⊂ (AIC) nên SB // (AIC).
Bài 1 trang 120 Toán 11 Tập 1: Trong không gian, hai đường thẳng song song với nhau khi và chỉ khi:
Bài 3 trang 120 Toán 11 Tập 1: Trong không gian, đường thẳng song song với mặt phẳng khi và chỉ khi:
Bài 4 trang 120 Toán 11 Tập 1: Trong không gian, hai mặt phẳng song song với nhau khi và chỉ khi:
Xem thêm các bài giải sách giáo khoa Toán 11 Cánh Dều hay, chi tiết khác:
Bài 2: Hai đường thẳng song song trong không gian
Bài 3: Đường thẳng và mặt phẳng song song
Bài 4: Hai mặt phẳng song song
Bài 5: Hình lăng trụ và hình hộp
Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.