Toptailieu biên soạn và giới thiệu giải Sách bài tập Toán 8 Bài tập cuối chương 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 8 Bài tập cuối chương 1.

SBT Toán 8 (Chân trời sáng tạo) Bài tập cuối chương 1

SBT Toán 8 Chân trờ sáng tạo trang 26

Câu 1 trang 26 sách bài tập Toán 8 Tập 1: Bậc của đơn thức 2x²y(2y²)² là

A. 2.

B. 5.

C. 8.

D. 7.

Lời giải:

Đáp án đúng là: D

Ta có: 2x²y(2y²)² = 2x²y.4y⁴ = 8x²y⁵, bậc của 8x²y⁵ là 7.

Câu 2 trang 26 sách bài tập Toán 8 Tập 1: Kết quả của phép nhân (4x – y)(y + 4x) là

A. 16x² – y².

B. y² – 16x².

C. 4x² – y².

D. 16x² – 8xy + y².

Lời giải:

Đáp án đúng là: A

Ta có: (4x – y)(y + 4x) = (4x – y)(4x + y) = (4x)² ‒ y² = 16x² – y².

Câu 3 trang 26 sách bài tập Toán 8 Tập 1: Thực hiện phép nhân (a² – 2a + 4)(a + 2), ta nhận được

A. a³ – 8.

B. a³ + 8.

C. (a – 2)³.

D. (a + 2)³.

Lời giải:

Đáp án đúng là: B

Ta có:

(a² – 2a + 4)(a + 2)

= (a + 2)(a² – 2.a + 2²)

= a³ + 2³

= a³ + 8.

Câu 4 trang 26 sách bài tập Toán 8 Tập 1: Phân tích đa thức 16x² – y⁴ thành nhân tử, ta nhận được

A. (4x² – y²)(4x² + y²).

B. x²(2 – y)(2 + y)(4x + y²).

C. (y² + 4x)(y² – 4x).

D. (4x – y²)(4x + y²).

Lời giải:

Đáp án đúng là: D

Ta có: 16x² – y⁴ = (4x)² ‒ (y²)² = (4x ‒ y²)(4x + y²).

Câu 5 trang 26 sách bài tập Toán 8 Tập 1: Phân tích đa thức x²(x + 1) – x(x + 1) thành nhân tử, ta nhận được

A. x.

B. x(x + 1).

C. x(x – 1)(x + 1).

D. x(x + 1)².

Lời giải:

Đáp án đúng là: C

Ta có: x²(x + 1) – x(x + 1) = (x + 1)(x² ‒ x) = x(x + 1)(x ‒1).

Câu 6 trang 26 sách bài tập Toán 8 Tập 1: Phân tích đa thức 5x – 5y + ax – ay thành nhân tử, ta nhận được

A. (5 + a)(x – y).

B. (5 – a)(x + y).

C. (5 + a)(x + y).

D. 5(x – y + a).

Lời giải:

Đáp án đúng là: A

Ta có: 5x – 5y + ax – ay = (5x – 5y) + (ax – ay)

= 5(x ‒ y) + a(x ‒ y) = (x ‒ y)(5 + a).

Câu 7 trang 26 sách bài tập Toán 8 Tập 1: Rút gọn phân thức $\frac{a\left(7-b\right)}{b\left(b^2-49\right)}$,ta nhận được

A. $\frac{a}{b\left(b-7\right)}$.

B. $\frac{a}{b\left(b+7\right)}$.

C. $-\frac{a}{b\left(b+7\right)}$.

D. $\frac{a}{b\left(7-b\right)}$.

Lời giải:

Đáp án đúng là: C

Ta có: $\frac{a\left(7-b\right)}{b\left(b^2-49\right)}=\frac{-a\left(b-7\right)}{b\left(b-7\right)\left(b+7\right)}=\frac{-a}{b\left(b+7\right)}$.

Câu 8 trang 26 sách bài tập Toán 8 Tập 1: Kết quả của phép trừ $\frac{a^2+2ab}{a-2b}-\frac{6ab-4b^2}{a-2b}$ là

A. a + 2b.

B. a – 2b.

C. 2.

D. $\frac{a^2-4ab-4b^2}{a-2b}$.

Lời giải:

Đáp án đúng là: B

Ta có: $\frac{a^2+2ab}{a-2b}-\frac{6ab-4b^2}{a-2b}=\frac{a^2+2ab-\left(6ab-4b^2\right)}{a-2b}$

$=\frac{a^2+2ab-6ab+4b^2}{a-2b}=\frac{a^2-4ab+4b^2}{a-2b}$

$=\frac{{\left(a-2b\right)}^2}{a-2b}=a-2b$.

Câu 9 trang 26 sách bài tập Toán 8 Tập 1: Kết quả của phép trừ $\frac{2b}{a^2+ab}-\frac{2a}{b^2+ab}$ là

A. $\frac{2\left(a+b\right)}{ab}$.

B. $\frac{2\left(a^2+b^2\right)}{ab}$.

C. $\frac{2\left(a-b\right)}{ab}$.

D. $\frac{2\left(b-a\right)}{ab}$.

Lời giải:

Đáp án đúng là: D

Ta có: $\frac{2b}{a^2+ab}-\frac{2a}{b^2+ab}=\frac{2b}{a\left(a+b\right)}-\frac{2a}{b\left(a+b\right)}$

$=\frac{2b.b-2a.a}{ab\left(a+b\right)}=\frac{2b^2-2a^2}{ab\left(a+b\right)}$

$=\frac{2\left(b-a\right)\left(b+a\right)}{ab\left(a+b\right)}=\frac{2\left(b-a\right)}{ab}$.

Câu 10 trang 26 sách bài tập Toán 8 Tập 1: Kết quả của phép chia $\frac{x^2-y^2}{6xy}:\frac{x-y}{3y}$ là

A. $\frac{x+y}{2x}$.

B. $\frac{x+y}{18x}$.

C. $\frac{2\left(x+y\right)}{x}$.

D. $\frac{x+y}{18x{y}^2}$.

Lời giải:

Đáp án đúng là: A

Ta có: $\frac{x^2-y^2}{6xy}:\frac{x-y}{3y}=\frac{x^2-y^2}{6xy}.\frac{3y}{x-y}$

$=\frac{\left(x-y\right)\left(x+y\right)}{6xy}.\frac{3y}{x-y}=\frac{x+y}{2x}$.

SBT Toán 8 Chân trờ sáng tạo trang 27

Bài 11 trang 27 sách bài tập Toán 8 Tập 1: Thu gọn các đa thức sau:

a) ab(3a – 2b) – ab(3b – 2a);

b) (a – 4b)(a + 2b) + a(a + 2b).

Lời giải:

a) Cách 1:

ab(3a – 2b) – ab(3b – 2a)

= 3a²b – 2ab² – 3ab² + 2a²b

= (3a²b + 2a²b) + (– 2ab² – 3ab²)

= 5a²b – 5ab².

Cách 2:

ab(3a – 2b) – ab(3b – 2a)

= ab[(3a ‒ 2b) ‒ (3b ‒ 2a)]

= ab(3a ‒ 2b ‒ 3b + 2a)

= ab(5a ‒ 5b) = 5a²b ‒ 5ab².

b) Cách 1:

(a – 4b)(a + 2b) + a(a + 2b)

= a(a + 2b) – 4b(a + 2b) + a² + 2ab

= a² + 2ab – 4ab – 8b² + a² + 2ab

= (a² + a²) + (2ab – 4ab + 2ab) – 8b²

= 2a² – 8b².

Cách 2:

(a – 4b)(a + 2b) + a(a + 2b)

= (a + 2b)(a ‒ 4b + a)

= (a + 2b)(2a ‒ 4b)

= 2(a + 2b)(a ‒ 2b)

= 2[a² ‒ (2b)²] = 2(a² – 4b²)

= 2a² ‒ 8b².

Bài 12 trang 27 sách bài tập Toán 8 Tập 1: Thu gọn các biểu thức sau:

a) (a – 4)(a + 4) + (2a – 1)²;

b) (3a – b)² – (a – 2b)(2b – a).

Lời giải:

a) (a – 4)(a + 4) + (2a – 1)²

= a² ‒ 4² + (2a)² ‒2.2a + 1

= a² ‒ 16 + 4a² ‒ 4a + 1

= (a² + 4a²) ‒ 4a ‒16 + 1

= 5a² ‒ 4a ‒ 15.

b) (3a – b)² – (a – 2b)(2b – a)

= (3a – b)² – [‒(a – 2b)(a ‒ 2b)]

= (3a)²‒2.3a.b + b² + (a ‒ 2b)²

= 9a² ‒ 6ab + b² + a² ‒ 4ab + 4b²

= (9a² + a²) + (‒6ab ‒ 4ab) + (b² + 4b²)

= 10a² ‒ 10ab + 5b².

Bài 13 trang 27 sách bài tập Toán 8 Tập 1: Thực hiện các phép nhân sau:

a) (x + y + 1)(x + y – 1);

b) (x + y – 4)(x – y + 4).

Lời giải:

a) Cách 1:

(x + y + 1)(x + y – 1)

= x(x + y – 1) + y(x + y – 1) + (x + y – 1)

= x² + xy ‒ x + xy + y² ‒ y + x + y ‒ 1

= x² + y² + (xy + xy) + (‒x + x) + (‒y + y) ‒1

= x² + y² + 2xy ‒ 1.

Cách 2:

(x + y + 1)(x + y – 1)

= (x + y)² – 1

= x² + 2xy + y² – 1.

b) Cách 1:

(x + y – 4)(x – y + 4)

= x(x – y + 4) + y(x – y + 4) – 4(x – y + 4)

= x² ‒ xy + 4x + xy ‒ y² + 4y ‒ 4x + 4y ‒16

= x² ‒y² +(‒xy + xy) + (4x ‒ 4x) + (4y + 4y) ‒16

= x² ‒y² + 8y ‒16.

Cách 2:

(x + y – 4)(x – y + 4)

= [x + (y – 4)].[x – (y – 4)]

= x² – (y – 4)²

= x² – (y² – 8y + 16)

= x² ‒y² + 8y ‒16.

Bài 14 trang 27 sách bài tập Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 3(a – b) + 2(a – b)²;

b) (a + 2)² – (4 – a²);

c) a² – 2ab – 4a + 8b;

d) 9a² – 4b² + 4b – 1;

e) a²b⁴ – 81a²;

g) a⁶ – 1.

Lời giải:

a) 3(a – b) + 2(a – b)²

= (a ‒ b)[3 + 2(a ‒ b)]

= (a ‒ b)(3 + 2a ‒ 2b).

b) (a + 2)² – (4 – a²)

= (a + 2)²‒ (2 ‒ a)(2 + a)

= (a + 2)[(a + 2) ‒ (2 ‒ a)]

= (a + 2)(a + 2 ‒ 2 + a)

= 2a(a + 2).

c) a² – 2ab – 4a + 8b

= (a² – 2ab) – (4a ‒ 8b)

= a(a ‒ 2b) ‒ 4(a ‒ 2b)

= (a ‒ 2b)(a ‒ 4).

d) 9a² – 4b² + 4b – 1

= 9a² – (4b² – 4b + 1)

= (3a)² – (2b – 1)²

= (3a + 2b – 1)(3a – 2b + 1).

e) a²b⁴ – 81a²

= a²(b⁴ ‒ 81)

= a²[(b²)² ‒ 9²]

= a²(b² + 9)(b² ‒ 9)

= a²(b² + 9)(b² ‒3²)

= a²(b² + 9)(b ‒ 3)(b + 3).

g) a⁶ – 1

= (a³)² ‒ 1²

= (a³ ‒ 1)(a³ + 1)

= (a ‒ 1)(a² + a + 1)(a + 1)(a² ‒ a + 1).

Bài 15 trang 27 sách bài tập Toán 8 Tập 1: Tính:

a) $\left(a+1+\frac{1-2a^2}{a-1}\right):\left(1-\frac{1}{1-a}\right)$;

b) $\left(\frac{a}{b^2}-\frac{1}{a}\right):\left(\frac{1}{b}+\frac{1}{a}\right)$;

c) $\left(a-\frac{4ab}{a+b}+b\right).\left(a+\frac{4ab}{a-b}-b\right)$;

d) $ab+\frac{ab}{a+b}\left(\frac{a+b}{a-b}-a-b\right)$.

Lời giải:

a) $\left(a+1+\frac{1-2a^2}{a-1}\right):\left(1-\frac{1}{1-a}\right)$

$=\frac{(a+1)(a-1)+1-2a^2}{a-1}:\frac{1-a-1}{1-a}$

$=\frac{a^2-1+1-2a^2}{a-1}:\frac{-a}{1-a}$

$=\frac{-a^2}{a-1}.\frac{1-a}{-a}$

$=\frac{-a^2}{a-1}.\frac{a-1}{a}=-a$.

b) $\left(\frac{a}{b^2}-\frac{1}{a}\right):\left(\frac{1}{b}+\frac{1}{a}\right)$

$=\frac{a^2-b^2}{a{b}^2}:\frac{a+b}{ab}=\frac{\left(a+b\right)(a-b)}{a{b}^2}.\frac{ab}{a+b}$

$=\frac{\left(a+b\right)(a-b)ab}{a{b}^2\left(a+b\right)}=\frac{a-b}{b}$.

c) $\left(a-\frac{4ab}{a+b}+b\right).\left(a+\frac{4ab}{a-b}-b\right)$

$=\left(\frac{a\left(a+b\right)}{a+b}-\frac{4ab}{a+b}+\frac{b(a+b)}{a+b}\right).\left(\frac{a(a-b)}{a-b}+\frac{4ab}{a-b}-\frac{b(a-b)}{a-b}\right)$

$=\frac{a^2+ab-4ab+ab+b^2}{a+b}.\frac{a^2-ab+4ab-ab+b^2}{a-b}$

$=\frac{a^2-2ab+b^2}{a+b}.\frac{a^2+2ab+b^2}{a-b}$

$=\frac{{\left(a-b\right)}^2{\left(a+b\right)}^2}{(a+b)(a-b)}=(a+b)(a-b)=a^2-b^2$.

d) $ab+\frac{ab}{a+b}\left(\frac{a+b}{a-b}-a-b\right)$

$=ab+\frac{ab}{a+b}\left(\frac{a+b}{a-b}-\left(a+b\right)\right)$

$=ab+\frac{ab}{a+b}.\frac{a+b}{a-b}-\frac{ab}{a+b}.\left(a+b\right)$

$ab+\frac{ab}{a-b}-ab=\frac{ab}{a-b}$.

Bài 16 trang 27 sách bài tập Toán 8 Tập 1: Ở hình bên, độ dài các cạnh AB, BC và GH đã được cho theo a và b; hai cạnh CD và EF bằng nhau; ba cạnh AH, GF và ED bằng nhau.

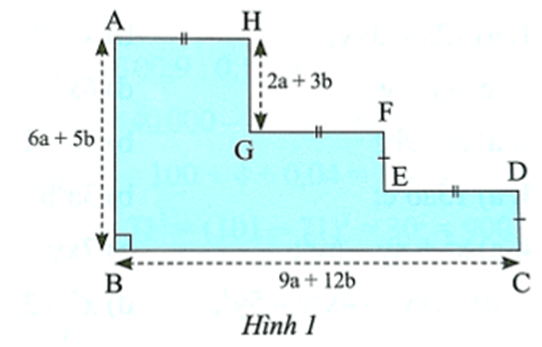
a) Tìm độ dài các cạnh AH, GF, ED.

b) Tìm độ dài các cạnh CD, EF.

c) Tính chu vi của hình bên.

Lời giải:

a) Ta có: AH = GF = ED và AH + GF + ED = BC

Nên $AH=GF=ED=\frac{BC}{3}=\frac{9a+12b}{3}=\frac{3(3a+4b)}{3}=3a+4b$.

b) Ta có:

EF + CD = AB ‒ GH

= 6a + 5b ‒ (2a + 3b) = 6a + 5b ‒ 2a ‒ 3b = 4a + 2b.

Mà EF = CD nên $EF=CD=\frac{4a+2b}{2}=\frac{2(2a+b)}{2}=2a+b$.

c) Chu vi hình vẽ là:

AB + BC + CD + DE + EF + FG + GH + HA

= AB + BC + (CD + EF + GH) + (DE + FG + HA)

= AB + BC + AB + BC

= 2AB + 2BC

= 2(6a + 5b) + 2(9a + 12b)

= 12a + 10b + 18a + 24b

= 30a + 34b.

Bài 17 trang 27 sách bài tập Toán 8 Tập 1: Lúc đầu người ta dự kiến thiết kế một chiếc hộp hình lập phương với độ dài mỗi cạnh là x (cm) (x > 3). Sau đó người ta điều chỉnh tăng chiều 3 cm, giảm chiều rộng 3 cm và giữ nguyên chiều cao. Sau khi điều chỉnh, thể tích của hộp giảm bao nhiêu, diện tích toàn phần của hộp giảm bao nhiêu so với dự kiến ban đầu? Áp dụng với x = 15 cm.

Lời giải:

Theo dự kiến, thể tích và diện tích toàn phần của hộp hình lập phương lần lượt là:

V = x³ (cm³); S = 6x² (cm²).

Sau khi điều chỉnh, hộp cso dạng hình hộp chữ nhật và có:

• Chiều dài là: x + 3 (cm).

• Chiều rộng là: x – 3 (cm).

• Thể tích là: V’ = (x + 3)(x ‒3)x = x(x² ‒ 9) = x³ – 9x (cm³).

• Diện tích một mặt đáy là: S_đáy = (x + 3)(x – 3) = x² – 9 (cm²).

• Diện tích xung quanh là:

S_xq = 2(x + 3 + x – 3).x = 2.2x.x = 4x² (cm²).

• Diện tích toàn phần là:

S’ = S_xq + 2S_đáy = 4x² + 2(x² – 9) = 4x² + 2x² – 18 = 6x² – 18 (cm²).

Từ đó, V ‒ V’ = x³ – (x³ ‒ 9x) = x³ – x³ + 9x = 9x (cm³).

Và S ‒ S’ = 6x² – (6x² ‒ 18) = 6x² ‒ 6x² + 18 = 18 (cm²).

Vậy sau khi điều chỉnh, thể tích của hộp giảm 9x (cm³) và diện tích toàn phần của hộp giảm 18 cm² so với dự kiến ban đầu.

Với x = 15, ta có:

V ‒ V’= 9.15 = 135 (cm³); S ‒ S’ = 18 (cm²).

Xem thêm các bài giải sách bài tậpToán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 6: Cộng, trừ phân thức

Bài 7: Nhân, chia phân thức

Bài 1: Hình chóp tam giác đều

Bài tập cuối chương 2

Bài 1: Định lí Pythagore