SBT Toán 11 (Chân trời sáng tạo) Bài 5: Phương trình lượng giác cơ bản

Ngọc Nguyễn Ngày: 13-03-2024 Lớp 11

217

Toptailieu.vn biên soạn và giới thiệu giải Sách bài tập Toán 11 Bài 5: Phương trình lượng giác cơ bản sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 11 Bài 5.

SBT Toán 11 (Chân trời sáng tạo) Bài 5: Phương trình lượng giác cơ bản

SBT Toán 11 trang 31 Tập 1 (Chân trời sáng tạo)

Bài 1 trang 30 SBT Toán 11 Tập 1: Giải các phương trình lượng giác sau:

a) $\sin (3 x + \frac{π}{6}) = \frac{\sqrt{3}}{2};$

b) cos(2x ‒ 30°) = ‒1;

c) 3sin(‒2x + 17°) = 4;

d) $\cos (3 x - \frac{7 π}{12}) = \cos (- x + \frac{π}{4});$

e) $\sqrt{3} \tan (x - \frac{π}{4}) - 1 = 0;$

g) $\cot (\frac{x}{3} + \frac{2 π}{5}) = \cot \frac{π}{5} .$

Lời giải:

a) $\sin (3 x + \frac{π}{6}) = \frac{\sqrt{3}}{2}$

$\Leftrightarrow \sin (3 x + \frac{π}{6}) = \sin (\frac{π}{3})$

$\Leftrightarrow 3 x + \frac{π}{6} = \frac{π}{3} + k 2 π, k \in ℤ$ hoặc $\Leftrightarrow 3 x + \frac{π}{6} = \frac{π}{3} + k 2 π, k \in ℤ$

$\Leftrightarrow x = \frac{π}{18} + k \frac{2 π}{3}, k \in ℤ$ và $x = \frac{π}{6} + k \frac{2 π}{3}, k \in ℤ$

Vậy phương trình có nghiệm là $x = \frac{π}{18} + k \frac{2 π}{3}, k \in ℤ$ và $x = \frac{π}{6} + k \frac{2 π}{3}, k \in ℤ$

b) cos(2x ‒ 30°) = ‒1

⇔ 2x ‒ 30° = 180° +k360π (k ∈ ℤ)

⇔ 2x = 210 + k360° (k ∈ ℤ)

⇔ x = 105° + k180° (k ∈ ℤ)

Vậy phương trình có nghiệm là x = 105° + k180° (k ∈ ℤ).

c) 3sin(‒2x + 17°) = 4

$\Leftrightarrow \sin (- 2 x + 17 °) = \frac{4}{3}$

Do $\frac{4}{3} > 1$ nên phương trình vô nghiệm.

d) $\cos (3 x - \frac{7 π}{12}) = \cos (- x + \frac{π}{4})$

$\Leftrightarrow 3 x - \frac{7 π}{12} = - x + \frac{π}{4} + k 2 π, k \in ℤ$ hoặc $\Leftrightarrow 3 x - \frac{7 π}{12} = - (- x + \frac{π}{4}) + k 2 π, k \in ℤ$

$\Leftrightarrow x = \frac{5 π}{24} + k \frac{π}{2}, k \in ℤ$ và $x = \frac{π}{6} + k π, k \in ℤ$

Vậy phương trình có nghiệm là $x = \frac{5 π}{24} + k \frac{π}{2}, k \in ℤ$ và $x = \frac{π}{6} + k π, k \in ℤ$

e) $\sqrt{3} \tan (x - \frac{π}{4}) - 1 = 0$

$\Leftrightarrow \tan (x - \frac{π}{4}) = \frac{1}{\sqrt{3}}$

$\Leftrightarrow \tan (x - \frac{π}{4}) = \tan \frac{π}{6}$

$\Leftrightarrow x - \frac{π}{4} = \frac{π}{6} + k π, k \in ℤ$

$\Leftrightarrow x = \frac{5 π}{12} + k π, k \in ℤ$

Vậy phương trình có nghiệm là $x = \frac{5 π}{12} + k π, k \in ℤ$

g) $\cot (\frac{x}{3} + \frac{2 π}{5}) = \cot \frac{π}{5}$

$\Leftrightarrow \frac{x}{3} + \frac{2 π}{5} = \frac{π}{5} + k π, k \in ℤ$

$\Leftrightarrow x = - \frac{3 π}{5} + k 3 π, k \in ℤ$

Vậy phương trình có nghiệm là $x = - \frac{3 π}{5} + k 3 π, k \in ℤ$

Bài 2 trang 31 SBT Toán 11 Tập 1: Giải các phương trình lượng giác sau:

a) cos(2x + 10°) = sin(50° ‒ x);

b) 8sin³x + 1 = 0;

c) (sinx + 3)(cotx ‒ 1) = 0;

d) tan(x ‒ 30°) ‒ cot50° = 0.

Lời giải:

a) cos(2x + 10°) = sin(50° ‒ x)

⇔ cos(2x + 10°) = cos(x + 40°)

⇔ 2x + 10° = x + 40°+ k360°, k ∈ ℤ hoặc 2x + 10° = ‒x ‒ 40°+ k360°, k ∈ ℤ

⇔ x = 30° + k360°, k ∈ ℤ hoặc $x = - \frac{1}{3} {.50}^{\circ} + k 120^{\circ}, k \in ℤ$ .

Vậy phương trình có các nghiệm là x = 30° + k360°, k ∈ ℤvà $x = - \frac{1}{3} \cdot 50^{\circ} + k 120^{\circ}, k \in ℤ .$

b) 8sin³x + 1 = 0

$\Leftrightarrow \sin^{3} x = - \frac{1}{8} \Leftrightarrow \sin x = - \frac{1}{2}$

$x = - \frac{π}{6} + k 2 π, k \in ℤ$ hoặc $x = π - (- \frac{π}{6}) + k 2 π, k \in ℤ$

$\Leftrightarrow x = - \frac{π}{6} + k 2 π, k \in ℤ$ hoặc $x = \frac{7 π}{6} + k 2 π, k \in ℤ$

Vậy phương trình có các nghiệm là $x = - \frac{π}{6} + k 2 π, k \in ℤ$ và $x = \frac{7 π}{6} + k 2 π, k \in ℤ$ .

c) (sinx + 3)(cotx ‒ 1) = 0

⇔ sinx + 3 = 0 hoặc cotx ‒ 1 = 0

⇔ sinx = ‒3 hoặc cotx = 1

Phương trình sinx = ‒3 vô nghiệm.

Phương trình cotx = 1 có nghiệm là $x = \frac{π}{4} + k π, k \in ℤ$ .

Vậy phương trình có các nghiệm là $x = \frac{π}{4} + k π, k \in ℤ$ .

d) tan(x ‒ 30°) ‒ cot50° = 0

⇔ tan(x ‒ 30°) = cot50°

⇔ tan(x ‒ 30°) = tan40°

⇔ x ‒ 30° = 40° + k180°, k ∈ ℤ

⇔ x = 70° + k180°, k ∈ ℤ

Vậy phương trình có các nghiệm là x = 70° + k180°, k ∈ ℤ.

Bài 3 trang 31 SBT Toán 11 Tập 1: Giải các phương trình lượng giác sau:

a) $\cos (x + \frac{π}{4}) + \cos (\frac{π}{4} - x) = 0;$

b) 2cos²x + 5sinx ‒ 4 = 0;

c) $\cos (3 x - \frac{π}{4}) + 2 \sin^{2} x - 1 = 0.$

Lời giải:

a) $cos (x + \frac{π}{4}) + cos (\frac{π}{4} - x) = 0$

$\Leftrightarrow cos (x + \frac{π}{4}) = - cos (\frac{π}{4} - x) \Leftrightarrow cos (x + \frac{π}{4}) = cos (\frac{3 π}{4} + x)$

$\Leftrightarrow x + \frac{π}{4} = \frac{3 π}{4} + x + k 2 π, k \in ℤ$ hoặc $x + \frac{π}{4} = - \frac{3 π}{4} - x + k 2 π, k \in ℤ$

$\Leftrightarrow x = - \frac{π}{2} + k π, k \in ℤ$

Vậy phương trình có các nghiệm là $x = - \frac{π}{2} + k π, k \in ℤ$

b) 2cos²x + 5sinx ‒ 4 = 0

⇔ 2(1 ‒ sin²x) + 5sinx ‒ 4 = 0

⇔ ‒2sin²x + 5sinx ‒ 2 = 0

⇔ sinx = 2 hoặc $sin x = \frac{1}{2} \Leftrightarrow sin x = \frac{1}{2}$

$\Leftrightarrow x = \frac{π}{6} + k 2 π, k \in ℤ$ hoặc $x = \frac{5 π}{6} + k 2 π, k \in ℤ$

Vậy phương trình có các nghiệm $x = \frac{π}{6} + k 2 π, k \in ℤ$ và $x = \frac{5 π}{6} + k 2 π, k \in ℤ$

c) $cos (3 x - \frac{π}{4}) + 2 {sin}^{2} x - 1 = 0$

$\Leftrightarrow cos (3 x - \frac{π}{4}) = 1 - 2 {sin}^{2} x \Leftrightarrow cos (3 x - \frac{π}{4}) = cos 2 x$

$\Leftrightarrow 3 x - \frac{π}{4} = 2 x + k 2 π, k \in ℤ$ hoặc $3 x - \frac{π}{4} = - 2 x + k 2 π, k \in ℤ$

$\Leftrightarrow x = \frac{π}{4} + k 2 π, k \in ℤ$ hoặc $x = \frac{π}{20} + k \frac{2 π}{5}, k \in ℤ$

Vậy phương trình có các nghiệm là $x = \frac{π}{4} + k 2 π, k \in ℤ$ và $x = \frac{π}{20} + k \frac{2 π}{5}, k \in ℤ$

Bài 4 trang 31 SBT Toán 11 Tập 1: Tìm tập xác định của hàm số lượng giác $y = \frac{s inx - 2 \cos 3 x}{s inx + \sin (2 x - \frac{π}{3})} .$

Lời giải:

Hàm số xác định khi và chỉ khi $sin x + sin (2 x - \frac{π}{3}) \neq 0.$

Ta có

$sin x + sin (2 x - \frac{π}{3}) = 0 \Leftrightarrow sin x = - sin (2 x - \frac{π}{3}) \Leftrightarrow sin x = sin (- 2 x + \frac{π}{3})$

$\Leftrightarrow x = - 2 x + \frac{π}{3} + k 2 π, k \in ℤ$ hoặc $x = π + 2 x - \frac{π}{3} + k 2 π, k \in ℤ$

$\Leftrightarrow x = \frac{π}{9} + k \frac{2 π}{3}, k \in ℤ$ hoặc $x = - \frac{2 π}{3} + k 2 π, k \in ℤ$

Do đó $sin x + sin (2 x - \frac{π}{3}) \neq 0$ khi và chỉ khi $x \neq \frac{π}{9} + k \frac{2 π}{3}, k \in ℤ và x \neq - \frac{2 π}{3} + k 2 π, k \in ℤ .$

Vậy tập xác định của hàm số là $D = ℝ ∖ (\frac{π}{9} + k \frac{2 π}{3}; - \frac{2 π}{3} + k 2 π ∣ k \in ℤ) .$

Bài 5 trang 31 SBT Toán 11 Tập 1: Tìm các nghiệm của mỗi phương trình sau trong khoảng (‒π; π)

a) $\sin (3 x - \frac{π}{3}) = 1;$

b) $2 \cos (2 x - \frac{3 π}{4}) = \sqrt{3};$

c) $\tan (x + \frac{π}{9}) = \tan \frac{4 π}{9} .$

Lời giải:

a) $\sin (3 x - \frac{π}{3}) = 1$

$\Leftrightarrow 3 x - \frac{π}{3} = \frac{π}{2} + k 2 π, k \in ℤ$

$\Leftrightarrow x = \frac{5 π}{18} + k \frac{2 π}{3}, k \in ℤ$

Với k = ‒1, ta có: $x = \frac{5 π}{18} - 1 \cdot \frac{2 π}{3} = - \frac{7 π}{18}$

Với k = 0, ta có: $x = \frac{5 π}{18} + 0 \cdot \frac{2 π}{3} = \frac{5 π}{18}$

Với k = 1, ta có: $x = \frac{5 π}{18} + 1 \cdot \frac{2 π}{3} = \frac{17 π}{18}$

Do phương trình có nghiệm thuộc (‒π; π) nên $x \in (- \frac{7 π}{18}; \frac{5 π}{18}; \frac{17 π}{18})$

b) $2 \cos (2 x - \frac{3 π}{4}) = \sqrt{3}$

$\Leftrightarrow \cos (2 x - \frac{3 π}{4}) = \frac{\sqrt{3}}{2}$

$\Leftrightarrow \cos (2 x - \frac{3 π}{4}) = \cos \frac{π}{6}$

$\Leftrightarrow 2 x - \frac{3 π}{4} = \frac{π}{6} + k 2 π, k \in ℤ$ hoặc $2 x - \frac{3 π}{4} = - \frac{π}{6} + k 2 π, k \in ℤ$

$\Leftrightarrow x = \frac{11 π}{24} + k π, k \in ℤ$ hoặc $x = \frac{7 π}{24} + k π, k \in ℤ$

Với k = ‒1, ta có $x = \frac{11 π}{24} + (- 1) \cdot π = - \frac{13 π}{24}$ hoặc $x = \frac{7 π}{24} + (- 1) \cdot π = \frac{- 17 π}{24}$

Với k = 0, ta có $x = \frac{11 π}{24} + 0 \cdot π = \frac{11 π}{24}$ hoặc $x = \frac{7 π}{24} + 0 \cdot π = \frac{7 π}{24}$

Với k = 1, ta có $x = \frac{11 π}{24} + 1 \cdot π = \frac{35 π}{24}$ hoặc $x = \frac{7 π}{24} + \cdot π = \frac{31 π}{24}$

Do phương trình có nghiệm thuộc (‒π; π) nên $x \in (- \frac{17 π}{24}; - \frac{13 π}{24}; \frac{7 π}{24}; \frac{11 π}{24})$

c) $\tan (x + \frac{π}{9}) = \tan \frac{4 π}{9}$

$\Leftrightarrow x + \frac{π}{9} = \frac{4 π}{9} + k π, k \in ℤ$

$\Leftrightarrow x = \frac{π}{3} + k π, k \in ℤ$

Với x = ‒1, ta có: $x = \frac{π}{3} + (- 1) \cdot π = \frac{- 2 π}{3}$

Với x = 0, ta có: $x = \frac{π}{3} + 0 \cdot π = \frac{π}{3}$

Với x = ‒1, ta có: $x = \frac{π}{3} + 1 \cdot π = \frac{4 π}{3}$

Do phương trình có nghiệm thuộc (‒π; π) nên $x \in (- \frac{2 π}{3}; \frac{π}{3})$

Bài 6 trang 31 SBT Toán 11 Tập 1: Tìm hoành độ các giao điểm của đồ thị các hàm số sau:

a) $y = \sin (2 x - \frac{π}{3})$ và $y = \sin (\frac{π}{4} - x);$

b) $y = \cos (3 x - \frac{π}{4})$ và $y = \cos (x + \frac{π}{6}) .$

Lời giải:

a) Hoành độ các giao điểm của đồ thị 2 hàm số là nghiệm của phương trình: $\sin (2 x - \frac{π}{3}) = \sin (\frac{π}{4} - x)$

$\Leftrightarrow 2 x - \frac{π}{3} = \frac{π}{4} - x + k 2 π, k \in ℤ$ hoặc $2 x - \frac{π}{3} = π - (\frac{π}{4} - x) + k 2 π, k \in ℤ$

$\Leftrightarrow x = \frac{7 π}{36} + k \frac{2 π}{3}, k \in ℤ$ hoặc $x = \frac{13 π}{12} + k 2 π, k \in ℤ$

Vậy hoành độ các giao điểm của đồ thị 2 hàm số là: $x = \frac{7 π}{36} + k \frac{2 π}{3}, k \in ℤ$ và $x = \frac{13 π}{12} + k 2 π, k \in ℤ$

b) Hoành độ các giao điểm của đồ thị 2 hàm số là nghiệm của phương trình:

$\cos (3 x - \frac{π}{4}) = \cos (x + \frac{π}{6})$

$\Leftrightarrow 3 x - \frac{π}{4} = x + \frac{π}{6} + k 2 π, k \in ℤ$ hoặc $3 x - \frac{π}{4} = - (x + \frac{π}{6}) + k 2 π, k \in ℤ$

$\Leftrightarrow x = \frac{5 π}{24} + k π, k \in ℤ$ hoặc $x = \frac{π}{48} + k \frac{π}{2}, k \in ℤ$

Vậy hoành độ các giao điểm của đồ thị 2 hàm số là: $x = \frac{5 π}{24} + k π, k \in ℤ$ và $x = \frac{π}{48} + k \frac{π}{2}, k \in ℤ$ .

Bài 7 trang 31 SBT Toán 11 Tập 1: Tìm hoành độ các giao điểm của đồ thị hàm số $y = \sin 3 x - \cos (\frac{3 π}{4} - x)$ với trục hoành.

Lời giải:

Hoành độ các giao điểm của đồ thị hàm số $y = \sin 3 x - \cos (\frac{3 π}{4} - x)$ với trục hoành là nghiệm của phương trình:

$\sin 3 x - \cos (\frac{3 π}{4} - x) = 0$

$\Leftrightarrow \sin 3 x = \cos (\frac{3 π}{4} - x)$

$\Leftrightarrow \sin 3 x = \cos (\frac{π}{2} + \frac{π}{4} - x)$

$\Leftrightarrow \sin 3 x = \sin (x - \frac{π}{4})$

$3 x = x - \frac{π}{4} + k 2 π, k \in ℤ$ hoặc $3 x = π - (x - \frac{π}{4}) + k 2 π, k \in ℤ$

$\Leftrightarrow x = - \frac{π}{8} + k π, k \in ℤ$ và $x = \frac{5 π}{16} + k \frac{π}{2}, k \in ℤ$ .

Vậy hoành độ các giao điểm của đồ thị hàm số $y = \sin 3 x - \cos (\frac{3 π}{4} - x)$ với trục hoành là $x = - \frac{π}{8} + k π, k \in ℤ$ và $x = \frac{5 π}{16} + k \frac{π}{2}, k \in ℤ$ .

Bài 8 trang 31 SBT Toán 11 Tập 1: Theo định luật khúc xạ ánh sáng, khi một tia sáng được chiếu tới mặt phân cách giữa hai môi trường trong suốt không đồng chất thì tỉ số $\frac{\sin i}{s inr},$ với i là góc tới và r là góc khúc xạ, là một hằng số phụ thuộc vào chiết suất của hai môi trường. Biết rằng khi góc tới là 45° thì góc khúc xạ là bao nhiêu? Làm tròn kết quả đến hàng phần trăm.

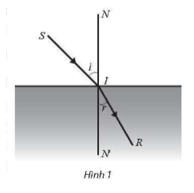
SBT Toán 11 (Kết nối tri thức) Bài 5: Phương trình lượng giác cơ bản (ảnh 1)

Lời giải:

Vì $\frac{sin 45 °}{sin 30 °} = \frac{sin 60 °}{sin r}$ nên $sin r = \frac{sin 60 ° sin 30 °}{sin 45 °} = \frac{\sqrt{6}}{4}$ . Suy ra r = 37,76°.

SBT Toán 11 trang 32 Tập 1 (Chân trời sáng tạo)

Bài 9 trang 32 SBT Toán 11 Tập 1: Một quả bóng được ném xiên một góc α (0° ≤ α ≤ 90°) từ mặt đất với tốc độ v₀ (m/s). Khoảng cách theo phương ngang từ vị trí ban đầu của quả bóng đến vị trí bóng chạm đất được tính bởi công thức $d = \frac{v_{0}^{2} \sin 2 α}{10} .$

a) Tính khoảng cách d khi bóng được ném đi với tốc độ ban đầu 10m/s và góc ném là 30° so với phương ngang.

b) Nếu tốc độ ban đầu của bóng là 10m/s thì cần ném bóng với góc bao nhiêu độ để khoảng cách d là 5 m?

Lời giải:

a) Khoảng cách d khi bóng được ném đi với tốc độ ban đầu 10m/s và góc ném là 30° so với phương ngang là:

$d = \frac{10^{2} \sin 2 \cdot 30 °}{10} = 5 \sqrt{3} \approx 8,66$ (m)

b) $d = \frac{v_{0}^{2} \sin 2 α}{10} .$ nên $\sin 2 α = \frac{10 d}{v_{0}^{2}}$

Nếu tốc độ ban đầu của bóng là 10m/s thì cần ném bóng với góc bao nhiêu độ để khoảng cách d là 5 m là:

$\sin 2 α = \frac{10 d}{v_{0}^{2}} = \frac{10 \cdot 5}{10^{2}} = \frac{1}{2}$

⇔ 2α = 30° hoặc 2α = 150°

⇔ α = 15° hoặc α = 75°

Bài 10 trang 32 SBT Toán 11 Tập 1: Chiều cao h(m) của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển động được cho bởi công thức $h (t) = 30 + 20 \sin (\frac{π}{25} t + \frac{π}{3}) .$

a) Cabin đạt độ cao tối đa là bao nhiêu?

b) Sau bao nhiêu giây thì cabin đạt độ cao 40 m lần đầu tiên?

Lời giải:

a) Cabin đạt độ cao tối đa khi $\sin (\frac{π}{25} t + \frac{π}{3}) = 1.$

Khi đó độ cao của cabin là h = 30 + 20.1 = 50 (m).

b) Thời gian để cabin đạt độ cao 40 m lần đầu tiênlà nghiệm của phương trình:

$30 + 20 \sin (\frac{π}{25} t + \frac{π}{3}) = 40$

$\Leftrightarrow \sin (\frac{π}{25} t + \frac{π}{3}) = \frac{1}{2}$

$\Leftrightarrow \sin (\frac{π}{25} t + \frac{π}{3}) = \sin \frac{π}{6}$

$\Leftrightarrow \frac{π}{25} t + \frac{π}{3} = \frac{π}{6} + k 2 π, k \in ℤ$ hoặc $\frac{π}{25} t + \frac{π}{3} = π - \frac{π}{6} + k 2 π, k \in ℤ$

$\Leftrightarrow t = - \frac{25}{6} + k 50, k \in ℤ$ hoặc $t = \frac{25}{2} + k 50, k \in ℤ$

⦁ Xét $t = - \frac{25}{6} + k 50, k \in ℤ$ ta có:

$- \frac{25}{6} + k 50 > 0 \Leftrightarrow k > \frac{1}{12}$ , k ∈ℤ nên k = 1. Do đó t = 44,8 s.

⦁ Xét $t = \frac{25}{2} + k 50, k \in ℤ$ ta có:

$t = \frac{25}{2} + k 50 > 0 \Leftrightarrow k > - \frac{1}{4}$ , k ∈ℤ nên k = 0. Do đó t = 12,5 s.

Do 12,5 < 44,8 nên sau 12,5 giây thì cabin đạt độ cao 40 m lần đầu tiên.

Xem thêm các bài SBT Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Hàm số lượng giác và đồ thị

Bài tập cuối chương 1 trang 32

Bài 1: Dãy số

Bài 2: Cấp số cộng

Bài 3: Cấp số nhân

Từ khóa :

Giải bài tập Toán 11

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương