Với Giải trang 9 SBT Toán lớp 11 trong Bài 1: Góc lượng giác Sách bài tập Toán lớp 11 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán lớp 11.

 SBT Toán 11 trang 9 Tập 1 (Chân trời sáng tạo)

Bài 4 trang 9 SBT Toán 11 Tập 1: Hãy tìm số đo α của góc lượng giác (Om, On), với ‒π ≤ α < π, biết một góc lượng giác cùng tia đầu Om và tia cuối On có số đo là:

a) $\frac{36\pi }{5};$          b) $\frac{-75\pi }{14};$                c) $\frac{39\pi }{8};$                          d) 2023π.

Lời giải:

a) Số đo α của các góc lượng giác bất kì có cùng tia đầu Om và tia cuối On sai khác nhau một bội nguyên của 2π nên có dạng là $\alpha =\frac{36\pi }{5}+k2\pi \left(k\in \mathbb{Z}\right)$

Ta có  ‒π ≤ α < π, suy ra $-\frac{41\pi }{5}\le k2\pi <\pi -\frac{36\pi }{5}$, suy ra $-\frac{41}{10}\le k<-\frac{31}{10}$.

Vì k ∈ ℤ nên k = ‒4.

Vậy $\alpha =\frac{36\pi }{5}+\left(-4\right).2\pi =\frac{-4\pi }{5}.$

b) Số đo α của các góc lượng giác bất kì có cùng tia đầu Om và tia cuối On sai khác nhau một bội nguyên của 2π nên có dạng là $\alpha =-\frac{75\pi }{14}+k2\pi \left(k\in \mathbb{Z}\right)$

Ta có  ‒π ≤ α < π, suy ra $-\pi +\frac{75\pi }{14}\le k2\pi <\pi +\frac{75\pi }{14}$, suy ra $\frac{61}{28}\le k<\frac{89}{28}$.

Vì k ∈ ℤ nên k = 3.

Vậy $\alpha =-\frac{75\pi }{14}+3.2\pi =\frac{9\pi }{14}.$

c) Số đo α của các góc lượng giác bất kì có cùng tia đầu Om và tia cuối On sai khác nhau một bội nguyên của 2π nên có dạng là $\alpha =\frac{39\pi }{8}+k2\pi \left(k\in \mathbb{Z}\right)$.

Ta có  ‒π ≤ α < π, suy ra $-\frac{47\pi }{8}\le k2\pi <\pi -\frac{31\pi }{8}$, suy ra $-\frac{47}{16}\le k<-\frac{31}{16}$.

Vì k ∈ ℤ nên k = ‒2.

Vậy $\alpha =\frac{39\pi }{8}+\left(-2\right).2\pi =\frac{7\pi }{8}.$

d) Số đo α của các góc lượng giác bất kì có cùng tia đầu Om và tia cuối On sai khác nhau một bội nguyên của 2π nên có dạng là α = 2023π + k2π (k ∈ ℤ).

Ta có  ‒π ≤ α < π, suy ra ‒2024π ≤ k2π < ‒2022π, suy ra ‒1012π ≤ k < ‒1011.

Vì k ∈ ℤ nên k = ‒1012.

Vậy α = 2023π + (‒1012).2π = ‒π.

Bài 5 trang 9 SBT Toán 11 Tập 1: Cho một góc lượng giác có số đo là 375°.

a) Tìm số lớn nhất trong các số đo của góc lượng giác cùng tia đầu, tia cuối với góc đó mà có số đo âm;

b) Tìm số nhỏ nhất trong các số đo của góc lượng giác cùng tia đầu, tia cuối với góc đó mà có số đo dương.

Lời giải:

Góc lượng giác cùng tia đầu, tia cuối với góc có số đo là 375° là 375° + k360° (k ∈ ℤ).

a) Góc này có số đo âm nên 375° + k360° < 0°, do đó $k<\frac{-375}{360}=\frac{-25}{24}$

Mà k ∈ ℤ và góc này có số đo âm lớn nhất nên k = −2

Khi đó góc cần tìm có số đo là 375° + (−2).360° = 345°.

b) Góc này có số đo dương nên 375° + k360° > 0°, do đó $k>\frac{-375}{360}=\frac{-25}{24}$

Mà k ∈ ℤ và góc này có số đo dương nhỏ nhất nên k = −1

Khi đó góc cần tìm có số đo là 375° + (−1).360° = 15°.

Bài 6 trang 9 SBT Toán 11 Tập 1: Viết công thức tổng quát của số đo góc lượng giác (Om, On) dưới dạng a° + k360° (k ∈ ℤ), với 0 ≤ a < 360°, biết một góc lượng giác với tia đầu Om, tia cuối On có số đo:

a) 1935°;                b) ‒450°;               c) ‒1440°;                     d) 754,5°

Lời giải:

a) Ta có 1935° = 135° + 5.360° nên công thức tồng quát của số đo góc lượng giác (Om, On) là (Om, On) = 135° + k360° (k ∈ ℤ).

b) Ta có ‒450° = 270° ‒ 2.360° nên công thức tồng quát của số đo góc lượng giác (Om, On) là (Om, On) = 270° +k360° (k ∈ ℤ).

c) Ta có ‒1440° = ‒4.360° nên công thức tổng quát của số đo góc lượng giác (Om, On) là (Om, On) =k360° (k ∈ ℤ).

d) Ta có 754,5° = 34,5° + 2.360° nên công thức tổng quát của số đo góc lượng giác (Om, On) là (Om, On) = 34,5° +k360° (k ∈ ℤ).

Bài 7 trang 9 SBT Toán 11 Tập 1: Biểu diễn các góc sau trên đường tròn lượng giác:

a) ‒1965°;                                    b) $\frac{48\pi }{5}.$

Lời giải:

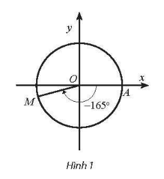
a) Ta có ‒1965° = ‒165° + (‒5).360°. Vậy điểm biểu diễn góc lượng giác có số đo ‒1965° là điếm M trên đường tròn lượng giác thuộc góc phần tư thứ III sao cho $\widehat{AOM}=165°$ như Hình 1.

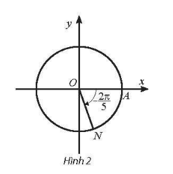
b) Ta có $\frac{48\pi }{5}=-\frac{2\pi }{5}+10\pi$. Vậy điểm biểu diễn góc lượng giác có số đo $\frac{48\pi }{5}$ là điểm N trên đường tròn lượng giác thuộc góc phần tư thứ III sao cho $\widehat{AON}=\frac{2\pi }{5}$ như Hình 2.

Bài 8 trang 9 SBT Toán 11 Tập 1:

a) Góc lượng giác ‒245° có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?

‒605°; ‒65°; 115°; 205°; 475°.

b) Góc lượng giác $\frac{24\pi }{5}$ có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?

$\frac{-16\pi }{5};\frac{-\pi }{5};\frac{14\pi }{5};\frac{29\pi }{5};\frac{53\pi }{10}.$

Lời giải:

a) Hiệu số đo của góc lượng giác ‒245° với góc lượng giác ‒605°; ‒65°; 115°; 205°; 475° là:

‒245° ‒ (‒605°) = 360°;

‒245°‒ (‒65°) = ‒180°;

‒245° ‒ 115° = ‒360°;

‒245° ‒ 205° = ‒450°;

‒245° ‒ 475° = ‒720° = 2.360°.

Vậy góc lượng giác ‒245° có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác là: ‒605°; 115°; 475°

b) Hiệu số đo của góc lượng giác $\frac{24\pi }{5}$ với góc lượng giác $\frac{-16\pi }{5};\frac{-\pi }{5};\frac{14\pi }{5};\frac{29\pi }{5};\frac{53\pi }{10}.$ là:

$\frac{24\pi }{5}-\left(-\frac{16\pi }{5}\right)=\frac{24\pi }{5}+\frac{16\pi }{5}=8\pi =4.2\pi ;$

$\frac{24\pi }{5}-\left(-\frac{\pi }{5}\right)=\frac{24\pi }{5}+\frac{\pi }{5}=5\pi =2.2\pi +\pi ;$

$\frac{24\pi }{5}-\frac{14\pi }{5}=2\pi ;$

$\frac{24\pi }{5}-\left(\frac{29\pi }{5}\right)=-\pi ;$

$\frac{24\pi }{5}-\frac{53\pi }{10}=\frac{48\pi }{10}-\frac{53\pi }{10}=-\frac{\pi }{2}.$

Vậy góc lượng giác $\frac{24\pi }{5}$ có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác là: $-\frac{16\pi }{5};\frac{14\pi }{5}.$

Bài 9 trang 9 SBT Toán 11 Tập 1: Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số đo có dạng là:

a) $\frac{\pi }{6}+k\pi \left(k\in \mathbb{Z}\right);$                         b) $\frac{\pi }{4}+k\frac{\pi }{2}\left(k\in \mathbb{Z}\right);$

Lời giải:

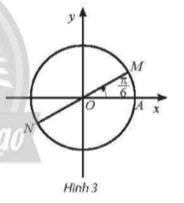
a) Trên đường tròn lượng giác, các góc có số đo $\frac{\pi }{6}+k\pi \left(k\in \mathbb{Z}\right)$ được biểu diễn bới hai điểm M và N như Hình 3.

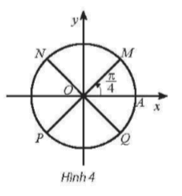
b) Trên đường tròn lượng giác, các góc có số đo $\frac{\pi }{4}+k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$ được biễu diễn bởi bốn điểm M, N, P, Q như Hình 4.

Bài 10 trang 9 SBT Toán 11 Tập 1: Trong hình bên, các điểm M, A’, N tạo thành ba đỉnh của một tam giác đều. Vị trí các điểm M, A’, N trên đường tròn lượng giác có thể được biểu diễn cho góc lượng giác nào sau đây?

$\frac{\pi }{3}+k\frac{2\pi }{3}\left(k\in \mathbb{Z}\right);-\pi +k\frac{2\pi }{3}\left(k\in \mathbb{Z}\right);-\frac{\pi }{3}+k\frac{\pi }{3}\left(k\in \mathbb{Z}\right).$

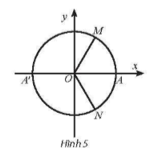
Lời giải:

Điểm M trên đường tròn lượng giác biểu diễn cho góc lượng giác có số đo: $\frac{\pi }{3}+k\frac{2\pi }{3}\left(k\in \mathbb{Z}\right);$

Điểm A’ trên đường tròn lượng giác biểu diễn cho góc lượng giác có số đo: $-\pi +k\frac{2\pi }{3}\left(k\in \mathbb{Z}\right)$

Điểm N trên đường tròn lượng giác biểu diễn cho góc lượng giác có số đo: $-\frac{\pi }{3}+k\frac{\pi }{3}\left(k\in \mathbb{Z}\right).$