Toptailieu.vn biên soạn và giới thiệu giải Sách bài tập Toán 11 Bài 1: Góc lượng giác sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 11 Bài 1.
Nội dung bài viết
SBT Toán 11 (Chân trời sáng tạo) Bài 1: Góc lượng giác
SBT Toán 11 trang 8 Tập 1 (Chân trời sáng tạo)
Bài 1 trang 8 SBT Toán 11 Tập 1: Đổi số đo của các góc sau đây sang radian:
a) 15°; b) 65°; c) ‒105°; d) (−5π)°
Lời giải:
a) 15°=15π180=π12;
b) 65°=65π180=13π36;
c) −105°=−105π180=−7π12;
d) (−5π)=(−5π)π180=−5180=−136.
Bài 2 trang 8 SBT Toán 11 Tập 1: Đổi số đo của các góc sau đây sang độ:
a) 6; b) 4π15; c) −19π8; d) 53.
Lời giải:
a) 6rad=(6⋅180π)°=343,77°.
b) 4π15rad=(4π15⋅180π)°=48°.
c) −19π8=(−19π8⋅180π)°=−427,5°.
d) 53rad=(53⋅180π)°=95,49°.
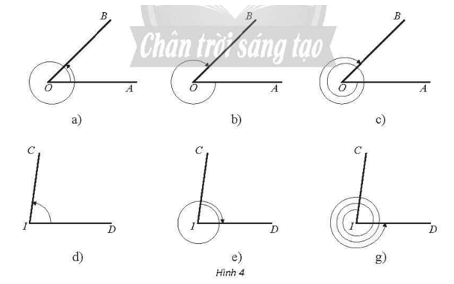
Lời giải:
a) Số đo góc lượng giác (OA, OB) trong Hình 4a là: π4+2π=9π4.
b) Số đo góc lượng giác (OA, OB) trong Hình 4b là: π4−2π=−7π4.
c) Số đo góc lượng giác (OA, OB) trong Hình 4c là: π4−2⋅2π=−15π4.
d) Số đo góc lượng giác (IC, ID) trong Hình 4d là: 82°.
e) Số đo góc lượng giác (IC, ID) trong Hình 4e là: ‒82° ‒ 360° = ‒442°.
g) Số đo góc lượng giác (IC, ID) trong Hình 4g là: ‒82 + 360°.3 = 998°.
SBT Toán 11 trang 9 Tập 1 (Chân trời sáng tạo)
a) 36π5; b) −75π14; c) 39π8; d) 2023π.
Lời giải:
a) Số đo α của các góc lượng giác bất kì có cùng tia đầu Om và tia cuối On sai khác nhau một bội nguyên của 2π nên có dạng là α=36π5+k2π(k∈ℤ)
Ta có ‒π ≤ α < π, suy ra −41π5≤k2π<π−36π5, suy ra −4110≤k<−3110.
Vì k ∈ ℤ nên k = ‒4.
Vậy α=36π5+(−4).2π=−4π5.
b) Số đo α của các góc lượng giác bất kì có cùng tia đầu Om và tia cuối On sai khác nhau một bội nguyên của 2π nên có dạng là α=−75π14+k2π(k∈ℤ)
Ta có ‒π ≤ α < π, suy ra −π+75π14≤k2π<π+75π14, suy ra 6128≤k<8928.
Vì k ∈ ℤ nên k = 3.
Vậy α=−75π14+3.2π=9π14.
c) Số đo α của các góc lượng giác bất kì có cùng tia đầu Om và tia cuối On sai khác nhau một bội nguyên của 2π nên có dạng là α=39π8+k2π(k∈ℤ).
Ta có ‒π ≤ α < π, suy ra −47π8≤k2π<π−31π8, suy ra −4716≤k<−3116.
Vì k ∈ ℤ nên k = ‒2.
Vậy α=39π8+(−2).2π=7π8.
d) Số đo α của các góc lượng giác bất kì có cùng tia đầu Om và tia cuối On sai khác nhau một bội nguyên của 2π nên có dạng là α = 2023π + k2π (k ∈ ℤ).
Ta có ‒π ≤ α < π, suy ra ‒2024π ≤ k2π < ‒2022π, suy ra ‒1012π ≤ k < ‒1011.
Vì k ∈ ℤ nên k = ‒1012.
Vậy α = 2023π + (‒1012).2π = ‒π.
Bài 5 trang 9 SBT Toán 11 Tập 1: Cho một góc lượng giác có số đo là 375°.
a) Tìm số lớn nhất trong các số đo của góc lượng giác cùng tia đầu, tia cuối với góc đó mà có số đo âm;
b) Tìm số nhỏ nhất trong các số đo của góc lượng giác cùng tia đầu, tia cuối với góc đó mà có số đo dương.
Lời giải:
Góc lượng giác cùng tia đầu, tia cuối với góc có số đo là 375° là 375° + k360° (k ∈ ℤ).
a) Góc này có số đo âm nên 375° + k360° < 0°, do đó k<−375360=−2524
Mà k ∈ ℤ và góc này có số đo âm lớn nhất nên k = −2
Khi đó góc cần tìm có số đo là 375° + (−2).360° = 345°.
b) Góc này có số đo dương nên 375° + k360° > 0°, do đó k>−375360=−2524
Mà k ∈ ℤ và góc này có số đo dương nhỏ nhất nên k = −1
Khi đó góc cần tìm có số đo là 375° + (−1).360° = 15°.
a) 1935°; b) ‒450°; c) ‒1440°; d) 754,5°
Lời giải:
a) Ta có 1935° = 135° + 5.360° nên công thức tồng quát của số đo góc lượng giác (Om, On) là (Om, On) = 135° + k360° (k ∈ ℤ).
b) Ta có ‒450° = 270° ‒ 2.360° nên công thức tồng quát của số đo góc lượng giác (Om, On) là (Om, On) = 270° +k360° (k ∈ ℤ).
c) Ta có ‒1440° = ‒4.360° nên công thức tổng quát của số đo góc lượng giác (Om, On) là (Om, On) =k360° (k ∈ ℤ).
d) Ta có 754,5° = 34,5° + 2.360° nên công thức tổng quát của số đo góc lượng giác (Om, On) là (Om, On) = 34,5° +k360° (k ∈ ℤ).
Bài 7 trang 9 SBT Toán 11 Tập 1: Biểu diễn các góc sau trên đường tròn lượng giác:
a) ‒1965°; b) 48π5.
Lời giải:
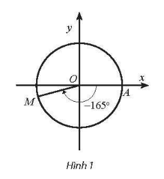
a) Ta có ‒1965° = ‒165° + (‒5).360°. Vậy điểm biểu diễn góc lượng giác có số đo ‒1965° là điếm M trên đường tròn lượng giác thuộc góc phần tư thứ III sao cho ^AOM=165° như Hình 1.
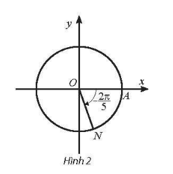
b) Ta có 48π5=−2π5+10π. Vậy điểm biểu diễn góc lượng giác có số đo 48π5 là điểm N trên đường tròn lượng giác thuộc góc phần tư thứ III sao cho ^AON=2π5 như Hình 2.
Bài 8 trang 9 SBT Toán 11 Tập 1:
‒605°; ‒65°; 115°; 205°; 475°.
b) Góc lượng giác 24π5 có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?
−16π5;−π5;14π5;29π5;53π10.
Lời giải:
a) Hiệu số đo của góc lượng giác ‒245° với góc lượng giác ‒605°; ‒65°; 115°; 205°; 475° là:
‒245° ‒ (‒605°) = 360°;
‒245°‒ (‒65°) = ‒180°;
‒245° ‒ 115° = ‒360°;
‒245° ‒ 205° = ‒450°;
‒245° ‒ 475° = ‒720° = 2.360°.
Vậy góc lượng giác ‒245° có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác là: ‒605°; 115°; 475°
b) Hiệu số đo của góc lượng giác 24π5 với góc lượng giác −16π5;−π5;14π5;29π5;53π10. là:
24π5−(−16π5)=24π5+16π5=8π=4.2π;
24π5−(−π5)=24π5+π5=5π=2.2π+π;
24π5−14π5=2π;
24π5−(29π5)=−π;
24π5−53π10=48π10−53π10=−π2.
Vậy góc lượng giác 24π5 có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác là: −16π5;14π5.
a) π6+kπ(k∈ℤ); b) π4+kπ2(k∈ℤ);
Lời giải:
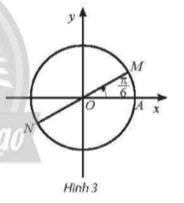
a) Trên đường tròn lượng giác, các góc có số đo π6+kπ(k∈ℤ) được biểu diễn bới hai điểm M và N như Hình 3.
b) Trên đường tròn lượng giác, các góc có số đo π4+kπ2(k∈ℤ) được biễu diễn bởi bốn điểm M, N, P, Q như Hình 4.
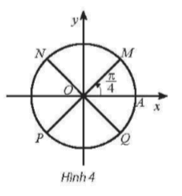
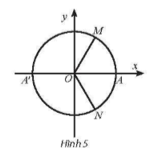
π3+k2π3(k∈ℤ);−π+k2π3(k∈ℤ);−π3+kπ3(k∈ℤ).
Lời giải:
Điểm M trên đường tròn lượng giác biểu diễn cho góc lượng giác có số đo: π3+k2π3(k∈ℤ);
Điểm A’ trên đường tròn lượng giác biểu diễn cho góc lượng giác có số đo: −π+k2π3(k∈ℤ)
Điểm N trên đường tròn lượng giác biểu diễn cho góc lượng giác có số đo: −π3+kπ3(k∈ℤ).
SBT Toán 11 trang 10 Tập 1 (Chân trời sáng tạo)
Lời giải:
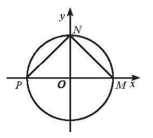
Dễ thấy M(1; 0), N(0; 1) và P(-1; 0).
Suy ra MN = NP = √2, MP = 2.
Do đó MNP là tam giác vuông cân tại N.
a) Sau 5 giây cánh quạt quay được một góc có số đo bao nhiêu radian?
b) Sau thời gian bao lâu cánh quạt quay được một góc có số đo 42π?
Lời giải:
a) Sau 1 giây, cánh quạt quay được 17560=3512(vòng) theo chiểu dương. Suy ra sau 1 giây, cánh quạt quay được một góc có số đo là 3512⋅2π=35π6.
Vậy sau 5 giây, cánh quạt quay được một góc có số đo là 35π6⋅5=175π6.
b) Thời gian để cánh quạt quay được một góc có số đo 42π là:
42π:35π6=7,2 (giây).
a) Sau 1 phút, van V đó quay được một góc có số đo là bao nhiêu radian?
b) Biết rằng bán kính của bánh xe là 35 cm. Độ dài quãng đường mà vận động viên đua xe đạp đã đi được trong một phút là bao nhiêu mét?
Lời giải:
a) Sau 1 giây, van V cúa bánh xe quay được 308=3,75(vòng).
Sau 1 phút, van V của bánh xe quay được 3,75. 60 = 225 (vòng).
Suy ra sau 1 phút, van V của bánh xe quay được một góc có số đo là 225.2π = 450π.
b) Mỗi góc ở tâm với số đo I rad chắn một cung có độ dài bằng bán kính bánh xe r = 0,35m. Do đó độ đài quãng đường mà vận động viên đua xe đạp đã đi được trong 1 phút là: 450π.0,35 ≈ 494,8 (m).
Xem thêm các bài SBT Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Giá trị lượng giác của một góc lượng giác
Bài 3: Các công thức lượng giác
Bài 4: Hàm số lượng giác và đồ thị
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.