Toptailieu.vn xin giới thiệu 30 câu trắc nghiệm Bài tập cuối chương III (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
30 câu trắc nghiệm Bài tập cuối chương III (có đáp án) chọn lọc
Câu 1. Tìm tập xác định D của hàm số y=f(x)=√x+2022+1xy=fx=x+2022+1x
A. D = ℝ \ {0};
B. D = ℝ \ {‒2022; 0};
C. D = [‒2022; +∞∞) \{0};
D. D = [‒2022; +∞∞).
Đáp án: C
Biểu thức y=f(x)=√x+2022+1x có nghĩa khi và chỉ khi:
Vậy tập xác định của hàm số này là D = [‒2022; +∞) \{0}.
Câu 2. Tập xác định của hàm số y=5−xx2−2xy=5−xx2−2xlà:
A. D = ℝ \ {0; 2};
B. D = ℝ \ {0; 2; 5};
C. D = ℝ \ (0; 2);
D. D = ℝ \ [0; 2];
Đáp án: A
Biểu thức y=5−xx2−2x có nghĩa khi và chỉ khi x2 – 2x ≠ 0
⇔x(x – 2) ≠ 0
Vậy tập xác định của hàm số đã cho là D = ℝ \ {0; 2}.
Câu 3. Cho hàm số f(x)=x+√x−3. Giá trị của f(f(4)) bằng:
A. 4;
B. 5;
C.5+√2;
D.5-√2;
Đáp án: C
Hàm số f(x)=x+√x−3 có tập xác định là D = [3; +∞)
Ta có: f(4)=4+√4−3=4+1=5
Do đó f(f(4))=f(5)=5+√5−3=5+√2
Vậy f(f(4))=5+√2.
Câu 4. Cho hàm số f(x) = 2x2 + ax + b (với a, b là tham số) thoả mãn f(2) = 11, f(3) = ‒7. Giá trị của 5a + 2b bằng:
A. ‒26;
B. ‒22;
C. 4;
D. 22.
Đáp án: B
Hàm số f(x) = 2x2 + ax + b có:
+) f(2) = 11 nên 2.22 + a.2 + b = 11 hay 2a + b = 3; (1)
+) f(3) = ‒7 nên 2.32 + a.3 + b = ‒7 hay 3a + b = ‒25. (2)
Cộng vế theo vế (1) và (2) ta được: 5a + 2b = ‒25 + 3 = ‒22.
Vậy: 5a + 2b = ‒22.
Câu 5. Cho hàm số y = 4x – 5 với x ∈ ℤ. Có bao nhiêu giá trị nguyên của x để ‒3 < y ≤ 10?
A. 2;
B. 3;
C. 4;
D. 5.
Đáp án: B
Để hàm số y = 4x – 5 (D = ℤ) thoả mãn điều kiện ‒3 < y ≤ 10 thì:
Mà x ∈ ℤ nên x ∈ {1;2;3}
Vậy có 3 giá trị x thoả mãn yêu cầu đề bài.
Câu 6. Một chất điểm chuyển động chậm dần đều với vận tốc v = 16t – 2t (cm/s), thời gian đo bằng giây. Tại thời điểm nào chất điểm đạt vận tốc 6 cm/s?
A. t = 2(s);
B. t = 4 (s);
C. t = 5 (s);
D. t = 10 (s).
Đáp án: C
Chất điểm chuyển động chậm dần đều với vận tốc v = 16t – 2t (cm/s), nên để chất điểm đạt vận tốc 6 cm/s thì 16t – 2t = 6
⇔⇔2t = 10
⇔⇔t = 5
Vậy t = 5 (s).
Câu 7. Cho hàm số y=x√m2+2022+m với x là biến số, m là tham số. Khẳng định nào sau đây là đúng?
A. Nếu m > 0 thì hàm số đồng biến trên ℝ, nếu m < 0 thì hàm số nghịch biến trên ℝ;
B. Nếu m > 0 thì hàm số nghịch biến trên ℝ, nếu m < 0 thì hàm số đồng biến trên ℝ;
C. Với mọi m hàm số luôn đồng biến trên ℝ;
D. Với mọi m hàm số luôn nghịch biến trên ℝ.
Đáp án: C
Xét hàm số y=x√m2+2022+m(D = ℝ) có hệ số của x là √m2+2022>0 với mọi m.
Do đó hàm số này đồng biến trên ℝ với mọi m.
Vậy ta chọn phương án C.
Câu 8. Cho hàm số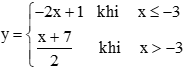
A. ‒2;
B. 0;
C. 1;
D. 3.
Đáp án: D
Trường hợp 1: Nếu xo ≤ ‒3 thì f(xo) = ‒2xo + 1
Để f(xo) = 5 thì ‒2xo + 1 = 5 ⇔⇔ xo = ‒2 (không thoả mãn xo ≤ ‒3)
Trường hợp 2: Nếu xo > ‒3 thì f(xo)=xo+72fxo=xo+72
Để f(xo) = 5 thì xo+72=5⇔xo+7=10⇔xo=3xo+72=5⇔xo+7=10⇔xo=3 (thoả mãn xo > ‒3)
Vậy xo = 3.
Câu 9. Cho hàm số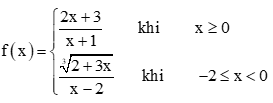
A. f(−1)=13;f(2)=73;
B.f(0)=2;f(−3)=√7;
C. f(‒1) không xác định; f(−3)=−1124;
D. f(−1)=√8;f(3)=0.
Đáp án: A
Với x = ‒1 ta có f(−1)=3√2+3.(−1)−1−2=−1−3=13
Với x = 2 ta có f(2)=2.2+32+1=73
Vậy ta chọn phương án A.
Câu 10. Cho hàm số y = f(x) có tập xác định là [‒3; 3] và có đồ thị hàm số như hình vẽ.
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biên trên khoảng (‒3; 1) và (1; 4);
B. Hàm số nghịch biến trên khoảng (‒2; 1);
C. Hàm số đồng biến trên khoảng (‒3; ‒1) và (1; 3);
D. Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.
Đáp án: C
Dựa vào đồ thị nhận thấy:
- Đồ thị hàm số có dạng đi lên từ trái sang phải trên các khoảng (‒3; ‒1) và (1; 3) nên hàm số đồng biến trên khoảng (‒3; ‒1) và (1; 3);
- Đồ thị hàm số có dạng đi xuống từ trái sang phải trên khoảng (‒1; 1) nên hàm số nghịch biến trên khoảng (‒1; 1).
- Đồ thị cắt trục hoành tại hai điểm phân biệt.
Vậy ta chọn phương án C.
Câu 11. Bảng biến thiên nào dưới đây là của hàm số y = ‒x2 + 2x + 1?
Đáp án: C
Đồ thị hàm số bậc hai y = ax2 + bx + c (với a ≠ 0) trong trường hợp a > 0 thì hàm số nghịch biến trên khoảng (−∞;−b2a)−∞;−b2a và đồng biến trên khoảng (−b2a;+∞)−b2a;+∞; trong trường hợp a < 0 thì hàm số đồng biến trên khoảng (−∞;−b2a)−∞;−b2a và nghịch biến trên khoảng (−b2a;+∞)−b2a;+∞.
Xét hàm số y = ‒x2 + 2x + 1 có các hệ số a = ‒1 < 0, b = 2 nên −b2a=1;−Δ4a=2−b2a=1;−Δ4a=2 .
Do đó hàm số đồng biến trên khoảng (‒∞∞; 1) và nghịch biến trên khoảng (1; +∞∞).
Vậy ta có bảng biến thiên của hàm số y = ‒x2 + 2x + 1 như sau:
Câu 12. Trục đối xứng của parabol y = ‒x2 + 5x + 3 là đường thẳng có phương trình:
A. x=54;x=54;
B. x=−52;x=−52;
C. x=−54;x=−54;
D. x=52.x=52.
Đáp án: D
Trục đối xứng của parabol y = ax2 + bx + c là đường thẳng x=−b2a.x=−b2a.
Hàm số y = ‒x2 + 5x + 3 có hệ số a = ‒1, b = 5, c = 3.
Do đó trục đối xứng của parabol y = ‒x2 + 5x + 3 là đường thẳng x=−5−2=52.x=−5−2=52.
Vậy trục đối xứng của parabol y = ‒x2 + 5x + 3 là đường thẳng có phương trình
Câu 13. Đồ thị dưới đây là của hàm số nào?
A. y = ‒x2 ‒2x + 3;
B. y = x2 + 2x – 2;
C. y = 2x2 – 4x – 2;
D. y = x2 – 2x – 1.
Đáp án: D
- Do parabol có bề lõm quay lên trên nên a > 0, ta loại A.
- Trục đối xứng của parabol là đường thẳng x=−b2a=1x=−b2a=1
Do đó ta loại B vì y = x2 + 2x – 2 có a = 1, b = 2 nên có trục đối xứng x=−22.2=−1≠1x=−22.2=−1≠1
- Quan sát đồ thị ta thấy x = 0 thì y = ‒1
Do đó ta loại C vì với x = 0 thì y = 2x2 – 4x – 2 = 2.02 – 4.0 – 2 = – 2 ≠ – 1.
Vậy đồ thị trên là của hàm số y = x2 – 2x – 1.
Câu 14. Cho hàm số y = (m – 1)x2 – 2(m – 2)x + m – 3 (với m ≠ 1) (P). Đỉnh của (P) là S(‒1; ‒2) thì m có giá trị bằng:
A.32;32;
B. 0;
C. 23;23;
D. 13.13.
Đáp án: A
Do đỉnh của (P) là S(‒1; ‒2) nên suy ra −1=m−2m−1−1=m−2m−1⇔⇔ m – 2 = ‒m + 1
⇔⇔ 2m = 3 ⇔m=32⇔m=32 (thoả mãn m ≠ 1)
Vậy m=32.m=32.
Câu 15. Hàm số y = ‒x2 + 2x + 3 có đồ thị là hình nào trong các hình sau?
A.
B.
C.
D.
Đáp án: A
Hàm số y = ‒x2 + 2x + 3 có a = ‒1 < 0, b = 2, c = 3 nên đồ thị lõm xuống dưới, do đó ta loại C và D.
Phương trình ‒x2 + 2x + 3 = 0 có hai nghiệm là x = 3, x = ‒1 nên đồ thị hàm số cắt trục Ox tại hai điểm (‒1; 0) và (3; 0).
Do đó ta loại phương án B.
Vậy ta chọn phương án A.
Câu 16. Cho hàm số y = ax2 + bx + c có đồ thị như hình dưới đây.
Khẳng định nào sau đây là đúng?
A. a < 0, b > 0, c > 0;
B. a > 0, b < 0, c > 0;
C. a < 0, b > 0, c < 0;
D. a > 0, b > 0, c < 0.
Đáp án: C
Nhìn vào đồ thị ta có:
- Bề lõm hướng xuống dưới nên a < 0.
- Hoành độ đỉnh x=−b2a>0⇒b2a<0⇒b>0x=−b2a>0⇒b2a<0⇒b>0 (vì a < 0).
- Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên y = a.02 + b.0 + c = c < 0.
Vậy a < 0, b > 0, c < 0.
Câu 17. Cho hàm số có đồ thị như hình bên dưới.
A. Hàm số nghịch biến trên khoảng (‒2; 1);
B. Hàm số đồng biến trên khoảng (‒∞∞; 1);
C. Hàm số nghịch biến trên khoảng (‒2; 0);
D. Hàm số đồng biến trên khoảng (‒∞∞; 0).
Đáp án: C
Trên khoảng từ (‒∞∞; ‒2) và (0; +∞∞) đồ thị hàm số đi lên từ trái sang phải nên hàm số đồng biến.
Trên khoảng (‒2; 0) thì đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
Vậy ta chọn phương án C.
Câu 18. Cho hàm số y = 2x2 – 4x + 3 có đồ thị là parabol (P). Mệnh đề nào sau đây sai?
A. (P) không có giao điểm với trục hoành;
B. (P) có đỉnh là S(1;1);
C. (P) có trục đối xứng là đường thẳng y = 1;
D. (P) đi qua điểm M(‒1;9).
Đáp án: C
Xét phương trình 2x2 – 4x + 3 = 0 vô nghiệm trên ℝ nên (P) không có giao điểm với trục hoành, do đó A là khẳng định đúng.
Hàm số y = 2x2 – 4x + 3 có các hệ số a = 2, b = ‒4, c = 3 nên đồ thị (P) có đỉnh là S(1;1), do đó B là khẳng định đúng.
(P) có trục đối xứng là đường thẳng x = 1 nên C là khẳng định sai.
Xét điểm M(‒1;9): thay x = ‒1 vào hàm số y = 2x2 – 4x + 3 ta được:
y = 2.(‒1)2 – 4.(‒1) + 3 = 9 nên (P) đi qua điểm M(‒1;9) do đó D là khẳng định đúng.
Vậy ta chọn C.
Câu 19. Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả là một cung parabol trong mặt phẳng với hệ tọa độ Oth , trong đó t là thời gian, kể từ khi quả bóng được đá lên: h là độ cao của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó ở độ cao 6m. Hãy tì hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo của quả bóng trong tình huống trên.
A. y = 4,9t2 + 12,2t + 1,2;
B. y = ‒4,9t2 + 12,2t + 1,2;
C. y = ‒4,9t2 + 12,2t ‒ 1,2;
D. y = ‒4,9t2 ‒ 12,2t + 1,2.
Đáp án: B
Tại t = 0 ta có y = h = 1,2;
Tại t = 1 ta có y = h = 8,5;
Tại t = 2 ta có y = h = 6.
Chọn hệ trục Oth như hình vẽ.
Parabol (P) có phương trình: y = at2 + bt + c, với a ≠ 0.
Giả sử tại thời điểm t’ thì quả bóng đạt độ cao lớn nhất h’.
Theo bài ra ta có: tại t = 0 thì h = 1,2 nên A(0; 1,2) ∈ (P) do đó thay toạ độ điểm A vào hàm số ta được: c = 1,2 (1)
Tại t = 1 thì h = 8,5 nên B(1; 8,5) ∈ (P) do đó thay toạ độ điểm B vào hàm số ta được: a + b + c = 8,5 (2)
Tại t = 2 thì h = 6 nên C(2; 6) ∈ (P) do đó thay toạ độ điểm C vào hàm số ta được: 4a + 2b + c = 6 (3)
Từ (1), (2) và (3) ta có hệ phương trình:
Vậy hàm số Parabol cần tìm có dạng: y = ‒4,9t2 + 12,2t + 1,2.
Câu 20. Một cửa hàng buôn giày nhập một đôi với giá là 40 đôla. Cửa hàng ước tính rằng nếu đôi giày được bán với giá x (x > 0) đôla thì mỗi tháng khách hàng sẽ mua (120 – x) đôi. Hỏi cửa hàng bán một đôi giày giá bao nhiều thì thu được nhiều lãi nhất?
A. 80 USD;
B. 160 USD;
C. 40 USD;
D. 240 USD.
Đáp án: A
Gọi y là số tiền lãi của cửa hàng bán giày.
Ta có y = (120 – x)(x – 40) = ‒x2 + 160x – 4800.
Để số tiền lãi thu được là nhiều nhất thì y đạt giá trị lớn nhất.
Hàm số trên có hệ số a = ‒1, b = 160, c = ‒4800 nên S(−b2a;−Δ4a)S−b2a;−Δ4a có toạ độ là S(80; 1600).
Vì a = ‒1 < 0 nên hàm số đạt giá trị lớn nhất tại 1600 khi x = 80.
Vậy cửa hàng lãi nhiều nhất khi bán đôi giày với giá 80 USD.
Câu 21. Cho hàm số y = 2x2 – 4x + 2. Chọn khẳng định sai:
A. Đồ thị hàm số đi qua điểm O(0; 0);
B. Đồ thị hàm số có đỉnh S(1; 0);
C. Đồ thị hàm số có trục đối xứng là x = 1;
D. Hàm số có tập xác định là D = ℝ.
Đáp án: A
Câu A: Thay x = 0; y = 0 vào hàm số đã cho ta có: 0 = 2. 02 – 4. 0 + 2 = 2 là mệnh đề sai. Vậy đồ thị hàm số không đi qua điểm O(0; 0). Khẳng định A sai.
Câu B: Hàm số y = 2x2 – 4x + 2 có các hệ số a = 2, b = ‒4, c = 2 nên đồ thị hàm số có đỉnh S(1; 0). Khẳng định B đúng.
Câu C: Hàm số y = 2x2 – 4x + 2 có các hệ số a = 2, b = ‒4, c = 2 nên đồ thị hàm số có trục đối xứng là x=−b2a=1x=−b2a=1 . Khẳng định C đúng.
Câu D: Hàm số bậc hai y = 2x2 – 4x + 2 có tập xác định là ℝ. Khẳng định D đúng.
Vậy ta chọn phương án A.
Câu 22. Tìm tập giá trị D của hàm số sau: y = f(x) = √2x+12x+1?
A. M = ℝ;
B. M = ℝ\{0};
C. M = [0; +∞);
D. M=(−12;+∞).M=−12;+∞.
Đáp án: C
Hàm số y = f(x) = √2x+12x+1xác định khi và chỉ khi √2x+12x+1 ≥ 0 ⇔⇔ x ≥ −12−12
Do đó hàm số y = f(x) = ≥ 0 với mọi giá trị x ≥
Vậy tập giá trị của hàm số là M = [0; +∞).
Câu 23. Đồ thị hàm số y = |2x + 3| là hình nào trong các hình sau:
A.
B.
C.
D.
Đáp án: B
Tập xác định của hàm số D = ℝ.
Ta có: y = |2x + 3| =
Ta vẽ đồ thị y = 2x + 3 với x≥−32x≥−32(d1)
Ta có bảng sau:
|
x |
0 |
|
|
y = f(x) |
3 |
0 |
Suy ra đồ thị hàm số y = f(x) = 2x + 3 với x≥−32x≥−32 là phần đồ thị nằm bên trên trục Ox và đi qua các điểm A(‒3232; 0) và B(0; 3).
Ta có đồ thị như sau:
Tương tự ta có đồ thị hàm số y = f(x) = - 2x - 3 với x < - là phần đồ thị nằm bên trên trục Ox và đi qua các điểm C(-2; 1) và D(-3; 3).
Kết hợp 2 đồ thị ta có đồ thị hàm số y = |2x + 3| là phần đồ thị nét liền nằm trên trục Ox.
Câu 24. Một ô tô đi từ A đến B với đoạn đường AB = s (km). Ô tô di chuyển thẳng đều với vận tốc là 40 km/h. Gọi mốc thời gian là lúc ô tô bắt đầu xuất phát từ A, t là thời điểm ô tô đi ở vị trí bất kì trên đoạn AB. Hãy xác định hàm số biểu thị mối quan hệ giữa s và t?
A. s=40ts=40t;
B. s = 40t;
C. t = 40s;
D. t=40st=40s.
Đáp án: B
Do thời gian luôn lớn hơn 0 nên tập xác định của hàm số ẩn t là D = (0; +∞)
Ta có công thức: Quãng đường = Vận tốc × Thời gian.
Do đó hàm số biểu thị mối quan hệ giữa s và t là: s = v. t = 40. t
Vậy s = 40t.
Câu 25. Tìm m để hàm số y = xx−mxx−mxác định trên khoảng (0; 5)?
A. 0 < m < 5;
B. m ≤ 0;
C. m ≥ 5;
D. m ≤ 0 hoặc m ≥ 5.
Đáp án: D
Hàm số y = xx−mxx−m xác định khi và chỉ khi x ≠ m.
Do đó để hàm số đã cho xác định trên khoảng (0; 5)
⇔ m ∉ (0; 5).
Do đó m ≤ 0 hoặc m ≥ 5.
Câu 26. Hàm số y =2x+1x−12x+1x−1 nghịch biến trên khoảng nào sau đây?
A. (1; 10);
B. (‒1; 5);
C. (0; 4);
D. (‒10; 10).
Đáp án: A
Ta thấy hàm số y = 2x+1x−12x+1x−1xác định khi và chỉ khi x ≠ 1.
Mà 1 thuộc các khoảng (-1; 5); (0; 4); (-10; 10).
Nên hàm số không xác định trên các khoảng (-1; 5); (0; 4); (-10; 10).
Suy ra các đáp án B, C, D là sai.
Vậy ta chọn phương án A.
Câu 27. Trong các điểm dưới đây, điểm nào thuộc đồ thị hàm số y = 2x2 – x + 1
A. M(0; 1);
B. N(0; 0);
C. P(1; 1);
D. Q(2; 2).
Đáp án: A
Câu A: Thay x = 0; y = 1 vào hàm số ta có: 1 = 2. 02 – 0 + 1 = 1 là mệnh đề đúng. Vậy điểm M thuộc đồ thị hàm số đã cho.
Câu B: Thay x = 0; y = 0 vào hàm số ta có: 0 = 2. 02 – 0 + 1 = 1 là mệnh đề sai. Vậy điểm N không thuộc đồ thị hàm số đã cho.
Câu C: Thay x = 1; y = 1 vào hàm số ta có: 1 = 2. 12 – 1 + 1 = 2 là mệnh đề sai. Vậy điểm P không thuộc đồ thị hàm số đã cho.
Câu D: Thay x = 2; y = 2 vào hàm số ta có: 2 = 2. 22 – 2 + 1 = 7 là mệnh đề sai. Vậy điểm Q không thuộc đồ thị hàm số đã cho.
Vậy ta chọn phương án A.
Câu 28. Theo tài liệu dân số và phát triển của Tổng cục dân số và kế hoạch hóa gia đình thì:
Dựa trên số liệu về dân số, kinh tế, xã hội của 85 nước trên thế giới, người ta xây dựng được hàm nêu lên mối quan hệ giữa tuổi thọ trung bình của phụ nữ (y) và tỷ lệ biết chữ của họ (x) như sau: y = 47,17 + 0,307x. Trong đó y là số năm (tuổi thọ), x là tỷ lệ phần trăm biết chữ của phụ nữ. Theo báo cáo của Bộ Giáo dục và Đào tạo năm học 2015 ‒ 2016, tỷ lệ biết chữ đã đạt 96,83% trong nhóm phụ nữ Việt Nam tuổi từ 15 đến 60. Hỏi với tỷ lệ biết chữ của phụ nữ Việt Nam như trên thì nhóm này có tuổi thọ bao nhiêu?
A. 67,89 tuổi;
B. 76,89 tuổi;
C. 76,98 tuổi;
D. 77,01 tuổi.
Đáp án: B
Thay x = 96,83 vào công thức y = 47,17 + 0,307x ta được:
y = 47,17 + 0,307. 96,83 = 47,17 + 29,72 = 76,89 (năm)
Vậy nhóm này có tuổi thọ 76,89 tuổi.
Câu 29. Một chiếc cổng hình parabol có dạng đồ thị giống đồ thị hàm số y = −12−12x2 như hình vẽ. Cổng có chiều rộng d = 8 m. Tính chiều cao h của cổng.
A. h = 4m
B. h = 8m
C. h = 10m
D. h = 16m
Đáp án: B
Gọi A là 1 điểm nằm ở bên phải chân cổng.
Hoành độ điểm A là bằng một nửa chiều rộng của cổng.
Tung độ của điểm A bằng chiều cao của cổng.
Parabol (P): y = −12−12x2 có d = 8 m, suy ra xA=d2=4xA=d2=4 .
A thuộc (P) suy ra yA = −12−12. 42 = ‒8.
Vậy chiều cao của cổng là h = 8 m.
Câu 30. Hình nào sau đây là đồ thị của hàm số y=−12x2+xy=−12x2+x?
A.
B.
C.
D.
Đáp án: A
Hàm số y=−12x2+xy=−12x2+x có các hệ số a = −12−12< 0, b = 1, c = 0
- Vì a = < 0 nên đồ thị hàm số có bề lõm quay xuống dưới, ta loại B và C.
- Đồ thị có toạ độ đỉnh S với xS=−b2a=1;xS=−b2a=1;tung độ yS=−Δ4a=12yS=−Δ4a=12 hay S(1;12).S1;12.Do đó ta loại A.
Vậy ta chọn D.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.