Toptailieu.vn xin giới thiệu 15 câu trắc nghiệm Hai dạng phương trình quy về phương trình bậc hai (Cánh diều) có đáp án - Toán 10 chọn lọc, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
15 câu trắc nghiệm Hai dạng phương trình quy về phương trình bậc hai (Cánh diều) có đáp án - Toán 10
Câu 1: Phương trình x4 − 6x2 – 7 = 0 có bao nhiêu nghiệm?
A. 0
B. 1
C. 2
D. 4
Lời giải:
Đặt x2 = t (t ≥ 0) ta được phương trình t2 – 6t – 7 = 0 (*)
Nhận thấy a – b + c = 1 + 6 – 7 = 0 nên phương trình (*) có hai nghiệm t1 = −1 (L); t2 = 7 (N)
Thay lại cách đặt ta có x2 = 7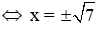 
Vậy phương trình đã cho có hai nghiệm
Đáp án cần chọn là: C
Câu 2: Phương trình 2x4 − 9x2 + 7 = 0 có bao nhiêu nghiệm?
A. 0
B. 1
C. 2
D. 4
Lời giải:
Đặt x2 = t ta được phương trình 2t2 – 9t + 7 = 0 (*)
Nhận thấy a + b + c = 2 + (−9) + 7 = 0 nên phương trình (*) có hai nghiệm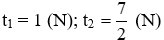 
Thay lại cách đặt ta có
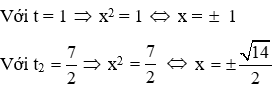
Vậy phương trình đã cho có bốn nghiệm phân biệt
Đáp án cần chọn là: D
Câu 3: Phương trình (x + 1)4 – 5(x + 1)2 – 84 = 0 có tổng các nghiệm là:
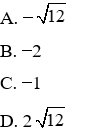
Lời giải:
Đặt (x + 1)2 = t (t ≥ 0) ta được phương trình t2 – 5t − 84 = 0 (*)
Ta có ∆ = 361 nên phương trình (*) có hai nghiệm
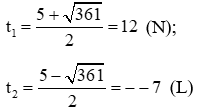
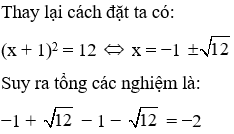
Đáp án cần chọn là: B
Câu 4: Phương trình (2x + 1)4 – 8(2x + 1)2 – 9 = 0 có tổng các nghiệm là:
A. 1
B. −2
C. −1
D. 2√2
Lời giải:
Đặt (2x + 1)2 = t (t ≥ 0) ta được phương trình t2 – 8t − 9 = 0 (*)
Ta có a – b + c = 1 – (−8) + (−9) = 0 nwn phương trình (*) có hai nghiệm
t1 = 1 (tm); t2 = −9 (ktm)
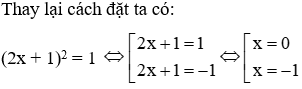
Suy ra tổng các nghiệm là 0 + (−1) = −1
Đáp án cần chọn là: C
Câu 5: Phương trình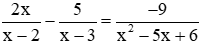 
có số nghiệm là:
A. 2
B. 1
C. 0
D. 3
Lời giải:
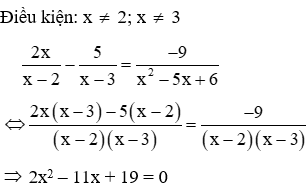
Nhận thấy ∆ = 112 – 4.9.2 = −31 < 0 nên phương trình 2x2 – 11x + 19 = 0 vô nghiệm
Suy ra phương trình đã cho vô nghiệm
Đáp án cần chọn là: C
Câu 6: Phương trình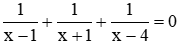 
có số nghiệm là:
A. 1
B. 0
C. 2
D. 3
Lời giải:
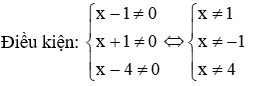
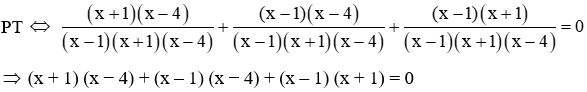
Đáp án cần chọn là: B
Câu 7: Phương trình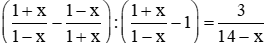 
có nghiệm là:
A. x = √2
B. x = 2
C. x = 3
D. x = 5
Lời giải:
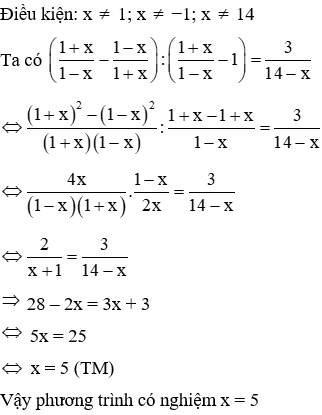
Đáp án cần chọn là: D
Câu 8: Phương trình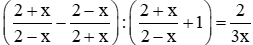 
có nghiệm là:
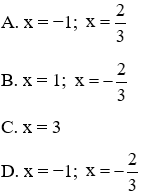
Lời giải:
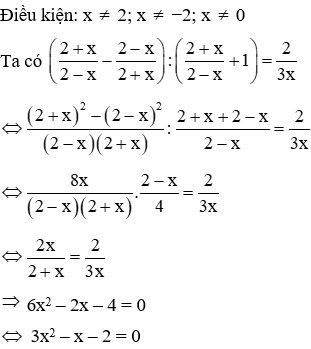
Phương trình này có a + b + c = 3 + (−1) + (−2) = 0 nên có hai nghiệm phân biệt là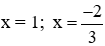 
(TM)
Vậy phương trình có hai nghiệm 
Đáp án cần chọn là: B
Câu 9: Tích các nghiệm của phương trình (x2 + 2x – 5)2 = (x2 − x + 5)2 là:
Lời giải:
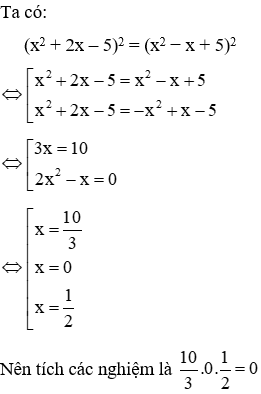
Đáp án cần chọn là: B
Câu 10: Tổng các nghiệm của phương trình (2x2 – 3)2 = 4(x – 1)2 là:
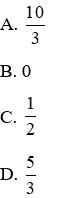
Lời giải:
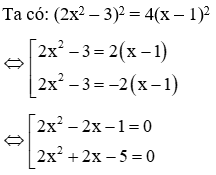
Phương trình 2x2 – 2x – 1 = 0 có ∆' = 3 > 0 nên có hai nghiệm
Phương trình 2x2 + 2x – 5 = 0 có ∆1 = 11 > 0 nên có hai nghiệm
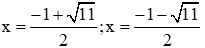
Nên tổng các nghiệm của phương trình đã cho là:
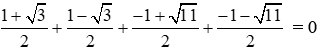
Đáp án cần chọn là: B
Câu 11: Số nghiệm của phương trình 3x3 + 3x2 + 5x + 5 = 0 là:
A. 2
B. 0
C. 1
D. 3
Lời giải:
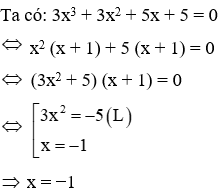
Vậy phương trình có nghiệm duy nhất x = −1
Đáp án cần chọn là: C
Câu 12: Nghiệm của phương trình x3 + 3x2 + x + 3 = 0 là:
A. x = ±1; x = −3
B. x = −1
C. x = 1
D. x = −3
Lời giải:
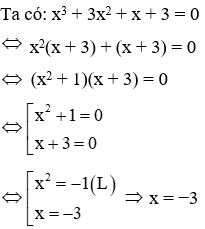
Vậy phương trình có nghiệm duy nhất x = −3
Đáp án cần chọn là: D
Câu 13: Tổng các nghiệm của phương trình x(x + 1)(x + 2)(x + 3) = 8 là:
A. −3
B. 3
C. 1
D. −4
Lời giải:
Ta có x(x + 1)(x + 2)(x + 3) = 8 ⇔ x (x + 3).(x + 1) (x + 2) = 8
⇔ (x2 + 3x)( x2 + 3x + 2) = 8
+) Với t = −3 ⇒ x2 + 3x + 1 = − 3 ⇔ x2 + 3x + 4 = 0, có ∆ = − 7 < 0 nên phương trình vô nghiệm.
Đáp án cần chọn là: A
Câu 14: Tổng các nghiệm của phương trình (x + 1)(x + 4)( x2 + 5x + 6) = 48 là:
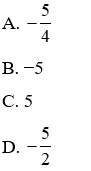
Lời giải:
Ta có (x + 1)(x + 4)( x2 + 5x + 6) = 48 ⇔ (x2 + 5x + 4) (x2 + 5x + 6) = 48
Đặt x2 + 5x + 5 = t, thu được phương trình:
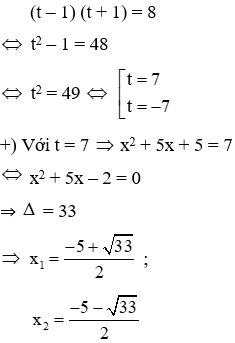
+) Với t = −7 ⇒ x2 + 5x + 5 = − 7 ⇔ x2 + 5x + 12 = 0 có ∆ = − 23 < 0 nên phương trình vô nghiệm.
Đáp án cần chọn là: B
Câu 15: Hai nghiệm của phương trình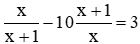 
là x1 > x2. Tính 3x1 + 4x2.
A. −3
B. 3
C. 7
D. −7
Lời giải:
Điều kiện: x 0; x −1
Đặt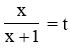 
(t ≥ 0), khi đó phương trình đã cho trở thành:
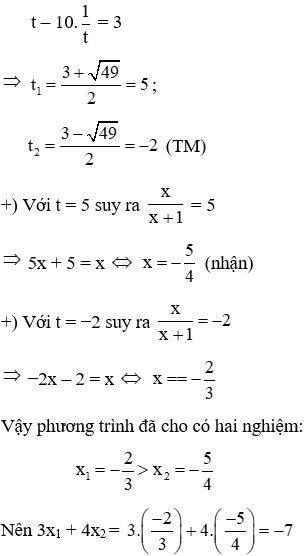
Đáp án cần chọn là: D
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
