Xét dấu của các tam thức bậc hai sau đây: f(x)= 2x^2+4x+2

Xét dấu của các tam thức bậc hai sau đây: f(x)= 2x^2+4x+2

Hoàng Huyền Trang Ngày: 04-10-2022 Lớp 10

725

Với giải Bài 4 trang 10 Toán 10 Tập 2 Chân trời sáng tạo chi tiết trong Bài 1. Số gần đúng và sai số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Xét dấu của các tam thức bậc hai sau đây: f(x)= 2x^2+4x+2

Bài 4 trang 10 Toán 10 Tập 2: Xét dấu của các tam thức bậc hai sau đây:

a) $f (x) = 2 x^{2} + 4 x + 2$

b) $f (x) = - 3 x^{2} + 2 x + 21$

c) $f (x) = - 2 x^{2} + x - 2$

d) $f (x) = - 4 x (x + 3) - 9$

e) $f (x) = (2 x + 5) (x - 3)$

Phương pháp giải

Bước 1: Tính và xác định dấu của biệt thức $Δ = b^{2} - 4 a c$

Bước 2: Xác định nghiệm của $f (x)$ (nếu có) $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

Bước 3: Xác định dấu của hệ số $a$

Bước 4: Xác định dấu của $f (x)$

Lời giải

a) $f (x) = 2 x^{2} + 4 x + 2$ có $Δ = 0$ , có nghiệm kép là $x_{1} = x_{2} = - 1$

và $a = 2 > 0$

Ta có bảng xét dấu như sau:

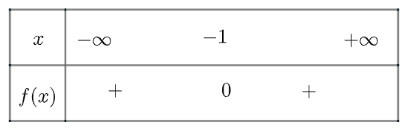
Bài 4 trang 10 Toán 10 Tập 2 Chân trời sáng tạo (ảnh 1)

Vậy $f (x)$ dương với mọi $x \neq - 1$

b) $f (x) = - 3 x^{2} + 2 x + 21$ có $Δ = 256 > 0$ , hai nghiệm phân biệt là $x_{1} = - \frac{7}{3}; x_{2} = 3$

và $a = - 3 < 0$

Ta có bảng xét dấu như sau:

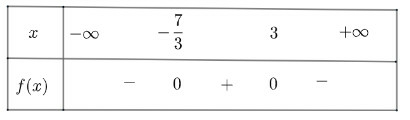
Bài 4 trang 10 Toán 10 Tập 2 Chân trời sáng tạo (ảnh 2)

Vậy $f (x)$ dương với $x \in (- \frac{7}{3}; 3)$ và âm khi $x \in (- \infty; - \frac{7}{3}) \cup (3; + \infty)$

c) $f (x) = - 2 x^{2} + x - 2$ có $Δ = - 15 < 0$ , tam thức vô nghiệm

và $a = - 2 < 0$

Ta có bảng xét dấu như sau:

Bài 4 trang 10 Toán 10 Tập 2 Chân trời sáng tạo (ảnh 3)

Vậy $f (x)$ âm với mọi $x \in R$

d) $f (x) = - 4 x (x + 3) - 9 = - 4 x^{2} - 12 x - 9$ có $Δ = 0$ , tam thức có nghiệm kép $x_{1} = x_{2} = - \frac{3}{2}$ và $a = - 4 < 0$

Ta có bảng xét dấu như sau

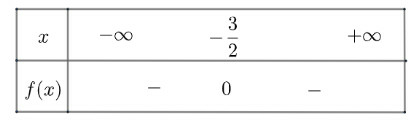
Bài 4 trang 10 Toán 10 Tập 2 Chân trời sáng tạo (ảnh 4)

Vậy $f (x)$ âm với mọi $x \neq - \frac{3}{2}$

e) $f (x) = (2 x + 5) (x - 3) = 2 x^{2} - x - 15$ có $Δ = 121 > 0$ , có hai nghiệm phân biệt $x_{1} = - \frac{5}{2}; x_{2} = 3$ và có $a = 2 > 0$

Ta có bảng xét dấu như sau

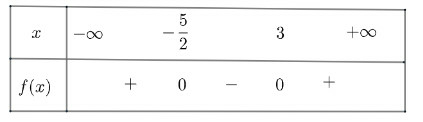
Bài 4 trang 10 Toán 10 Tập 2 Chân trời sáng tạo (ảnh 5)

Vậy $f (x)$ âm với $x \in (- \frac{5}{2}; 3)$ và dương khi $x \in (- \infty; - \frac{5}{2}) \cup (3; + \infty)$

Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:

HĐ Khám phá 1 trang 6 Toán 10 Tập 2: Đồ thị của hàm số $y = f (x) = - x^{2} + x + 3$ được biểu diễn trong hình 1...

Thực hành 1 trang 7 Toán 10 Tập 2: Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại $x = 1$ ...

Thực hành 2 trang 7 Toán 10 Tập 2: Tìm biệt thức và nghiệm của các tam thức bậc hai sau...

HĐ Khám phá 2 trang 8 Toán 10 Tập 2: Quan sát đồ thị của các hàm số bậc hai trong các hình thức dưới đây. Trong mỗi trường hợp, hãy cho biết...

Thực hành 3 trang 9 Toán 10 Tập 2: Xét dấu của các tam thức bậc hai sau...

Vận dụng trang 9 Toán 10 Tập 2: Xét dấu tam thức bậc hai $h (x) = - 0, 006 x^{2} + 1, 2 x - 30$ trong bài toán khởi động và cho biết ở khoảng cách nào tính từ đầu cầu O thì vòm cầu: cao hơn mặt cầu, thấp hơn mặt cầu...

Bài 1 trang 9 Toán 10 Tập 2: Đa thức nào sau đây là tam thức bậc hai?...

Bài 2 trang 9 Toán 10 Tập 2: Xác định giá trị của m để các đa thức sau là tam thức bậc hai...

Bài 3 trang 10 Toán 10 Tập 2: Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng...

Bài 5 trang 10 Toán 10 Tập 2: Độ cao (tính bằng mét) của một quả bóng so với vành rổ khi bóng di chuyển được x mét theo phương ngang được mô phỏng bằng hàm số $h (x) = - 0, 1 x^{2} + x - 1$ . Trong các khoảng nào của x thì bóng nằm: cao hơn vành rổ, thấp hơn vành rổ và ngang vành rổ? Làm tròn các kết quả đến hàng phần mười...

Bài 6 trang 10 Toán 10 Tập 2: Một khung dây thép hình chữ nhật có chiều dài 20 cm và chiều rộng 15 cm được uốn lại thành hình chữ nhật mới có kích thước $(20 + x)$ cm và $(15 - x)$ cm. Với x nằm trong các khoảng nào thì diện tích của khung sau khi uốn: tăng lên, không thay đổi, giảm đi?...

Bài 7 trang 10 Toán 10 Tập 2: Chứng minh rằng với mọi số thực m ta luôn có $9 m^{2} + 2 m > - 3$ ...

Bài 8 trang 10 Toán 10 Tập 2: Tìm giá trị của m để...

Từ khóa :

Giải bài tập Toán 10

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

298

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

319

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

347

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

295

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.