Với giải Bài 12 trang 92 SBT Toán 8 Tập 1 Cánh diều chi tiết trong Bài 3: Hình thang cân giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Cho hình thang cân ABCD có AB//CD, AB<CD, hai đường chéo AC và BD cắt nhau tại P
Bài 12 trang 92 SBT Toán 8 Tập 1: Cho hình thang cân ABCD có AB//CD,AB<CD, hai đường chéo AC và BD cắt nhau tại P, hai cạnh bên AD và BC kéo dài cắt nhau tại Q. Chứng minh PQ là đường trung trực của hai đáy hình thang cân ABCD.
Lời giải:
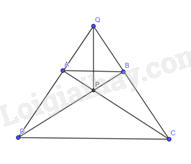
ΔACD=ΔBDC (c.g.c). Suy ra ^PCD=^PDC
Do đó, tam giác PCD cân tại P. Suy ra PC=PD
Mà AC=BD, suy ra PA=PB
Do AB//CD nên ^QAB=^ADC;^QBA=^BCD (các cặp góc đồng vị)
Mặt khác, ^ADC=^BCD nên ^QAB=^QBA
Do đó, tam giác QAB cân tại Q. Suy ra QA=QB
Mà AD=BC, suy ra QD=QC
Ta có: PA=PB,PC=PD và QA=QB,QC=QD nên PQ là đường trung trực của cả hai đoạn thẳng AB và CD.
Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:
Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.