Cho hình bình hành ABCD có BC=2AB. Gọi M, N lần lượt là trung điểm của BC, AD

Cho hình bình hành ABCD có BC=2AB. Gọi M, N lần lượt là trung điểm của BC, AD

Mai Hương Ngày: 25-01-2024 Lớp 8

142

Với giải Bài 43 trang 104 SBT Toán 8 Tập 1 Cánh diều chi tiết trong Bài tập cuối chương 5 giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Cho hình bình hành ABCD có BC=2AB. Gọi M, N lần lượt là trung điểm của BC, AD

Bài 43 trang 104 SBT Toán 8 Tập 1: Cho hình bình hành $A B C D$ có $B C = 2 A B$ . Gọi $M, N$ lần lượt là trung điểm của $B C, A D$

a) Chứng minh tứ giác $M B N D$ là hình bình hành.

b) Gọi $P$ là giao điểm của $A M$ và $B N, Q$ là giao điểm của $C N$ và $D M$ . Chứng minh tứ giác $P M Q N$ là hình chữ nhật.

c) Tìm điều kiện của hình bình hành $A B C D$ để tứ giác $P M Q N$ là hình vuông.

d) Tính diện tích của tứ giác $P M Q N$ , biết $A B = 2 c m, \hat{M A D} = 30^{\circ}$ .

Lời giải:

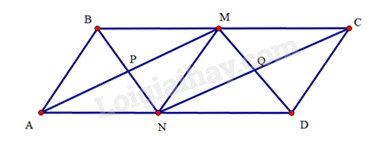
Sách bài tập Toán 8 (Cánh diều) Bài tập cuối chương 5 trang 103 (ảnh 5)

a) Do $A B C D$ là hình bình hành nên $B C / / A D$ và $B C = A D$

Mà $M \in B C, N \in A D$ nên $M B / / N D$

Lại có $M, N$ lần lượt là trung điểm của $B C, A D$ nên $M B = M C = \frac{1}{2} B C, N A = N D = \frac{1}{2} A$

Do đó $M B = M C = N A = N D$

Tứ goác $M B N D$ có $M B / / N D$ và $M B = N D$ nên là hình bình hành.

b) Tương tự câu a, ta chứng minh được $M A N C$ là hình bình hành.

Do $M B N D, M A N C$ đều là hình bình hành nên $P N / / M Q, P M / / N Q$ . Suy ra tứ giác $P M Q N$ là hình bình hành.

$Δ A B N = Δ M B N$ (c.g.c). Suy ra $A B = M N$ .

Tứ giác $A B M N$ có $A B = B M - M N = A N$ nên $A B M N$ là hình thoi. Suy ra $A M ⊥ B n$

Hình bình hành $P M Q N$ có $\hat{M P N} = 90^{\circ}$ nên $P M Q N$ là hình chữ nhật.

c) Để hình chữ nhật $P M Q N$ là hình vuông thì $P M = P N$ .

Mà $A B M N$ là hình thoi nên $A B M N$ là hình bình hành. Suy ra $A M, B N$ cắt nhau tại trung điểm $P$ của mỗi đường. mà $P M = P N$ , suy ra $A M = B N$

Hình bình hành $A B M N$ có $A M = B N$ nên $A B M N$ là hình chữ nhật

Suy ra $\hat{A B M} = 90^{\circ}$ hay $\hat{A B C} = 90^{\circ}$

Hình bình hành $A B C D$ có $\hat{A B C} = 90^{\circ}$ nên $A B C D$ là hình chữ nhật.

Dễ thấy, nếu hình bình hành $A B C D$ là hình chữ nhật và $B C = 2 A B$ thì $P M Q N$ là hình vuông.

Vậy điều kiện của hình bình hành $A B C D$ để $P M Q N$ là hình vuông là hình bình hành $A B C D$ là hình chữ nhật có $B C = 2 A B$ .

d) Ta có: $B M = A B$ nên $B M = 2 c m$

Do $A B M N$ là hình thoi nên $A M$ là tia phân giác của $\hat{B A N}$

Suy ra $\hat{B A N} = 2 \hat{M A D} = 60^{\circ}$

Tam giác $A B N$ có $A B = A N$ và $\hat{B A N} = 60^{\circ}$ nên tam giác $A B N$ đều.

Suy ra $B N = A N = A B = 2 c m$

Do $P$ là trung điểm của $B N$ nên $B P = N P = \frac{B N}{2} = 1 c m$

Trong tam giác $B M P$ vuông tại $P$ , ta có: $B M^{2} = B P^{2} + M P^{2}$

Suy ra $M P^{2} = B M^{2} - B P^{2} = 3$ . Do đó $M P = \sqrt{3}$ cm

Do $P M Q N$ là hình chữ nhật nên diện tích của $P M Q N$ là:

$M P . N P = \sqrt{3} .1 = \sqrt{3} (c m^{2})$ .

Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:

Bài 37 trang 103 SBT Toán 8 Tập 1: Cho hình bình hành $A B C D$ có $\hat{A} = 3 \hat{B}$ . Số đo các góc của hình bình hành $A B C D$ là:

Bài 38 trang 103 SBT Toán 8 Tập 1: Cho hình vuông $A B C D$ có độ dài bằng 8 cm. Độ dài đường chéo $A C$ là:

Bài 39 trang 103 SBT Toán 8 Tập 1: Cho tứ giác $A B C D$ có $E, F, G, H$ lần lượt là trung điểm của $A B, B C, C D, D A$ . Điều kiện của tứ giác $A B C D$ để tứ giác $E F G H$ là hình chữ nhật là:

Bài 40 trang 103 SBT Toán 8 Tập 1: Một công ti dự định làm một đường ống dẫn từ một nhà máu ở địa điểm $C$ trên bờ đến một địa điểm $B$ trên biển.

Bài 41 trang 104 SBT Toán 8 Tập 1: Cho tam giác $A B C$ vuông tại $A$ có đường cao $A H$ . Kẻ $H J$ vuông góc với $A B$ tại $J$ và $H K$ vuông góc với $A C$ tại $K$ .

Bài 42 trang 104 SBT Toán 8 Tập 1: Cho hình thang cân $A B C D$ có $A B / / C D, \hat{D} = 45^{\circ}$ . Kẻ $A H$ vuông góc với $C D$ tại $H$ . Lấy điểm $E$ thuộc cạnh $C D$ sao cho $H E = D H$ .

Bài 43 trang 104 SBT Toán 8 Tập 1: Cho hình bình hành $A B C D$ có $B C = 2 A B$ . Gọi $M, N$ lần lượt là trung điểm của $B C, A D$

Bài 44 trang 104 SBT Toán 8 Tập 1: Cho hình vuông $A B C D$ . Lấy điểm $M$ thuộc đường chéo $B D$ . Kẻ $M E$ vuông góc với $A B$ tại $E$ , $M F$ vuông góc với $A D$ tại $F$ .

Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:

Bài 7: Hình vuông

Bài 1: Thu thập và phân loại dữ liệu

Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ

Bài 3: Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ

Bài 4: Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản

Từ khóa :

Giải bài tập Toán 8

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

203

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

243

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

263

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

217

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.