Từ các công thức khai triển: (a + b)0 = 1; (a + b)1 = a + b; (a + b)2 = a2 + 2ab + b2;

Từ các công thức khai triển: (a + b)0 = 1; (a + b)1 = a + b; (a + b)2 = a2 + 2ab + b2;

Phạm Thị Huyền Trang Ngày: 12-12-2022 Lớp 10

470

Với giải Khám phá 2 trang 35 Chuyên đề Toán 10 Chân trời sáng tạo chi tiết trong Bài 4: Nhị thức Newton giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Chuyên đề Toán 10. Mời các bạn đón xem:

Giải bài tập Chuyên đề Toán lớp 10 Bài 4: Nhị thức Newton

Khám phá 2 trang 35 Chuyên đề Toán 10: Từ các công thức khai triển:

(a + b)⁰ = 1;

(a + b)¹ = a + b;

(a + b)² = a² + 2ab + b²;

(a + b)³ = a³ + 3a²b + 3ab² + b³;

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴;

(a + b)5 = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵;

các hệ số được viết thành bảng số như Hình 2 sau đây. Nếu sử dụng kí hiệu tổ hợp thì nhận được bảng như Hình 3.

(ảnh 1)

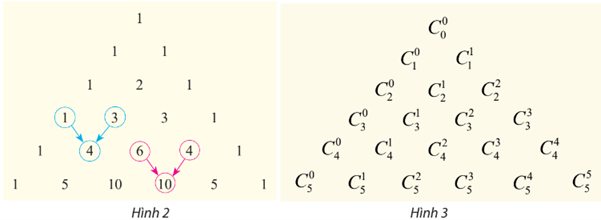
Từ các đẳng thức như

$\begin{matrix} C_{3}^{0} = C_{3}^{3} = 1, & C_{4}^{1} = C_{4}^{3} = 4, \\ C_{3}^{0} + C_{3}^{1} = C_{4}^{1}, & C_{4}^{2} + C_{4}^{3} = C_{5}^{3}, \end{matrix}$

có thể dự đoán rằng, với mỗi $n \in ℕ^{*}$

$C_{n}^{k} = C_{n}^{n - k} (0 \leq k \leq n);$

$C_{n}^{k - 1} + C_{n}^{k} = C_{n + 1}^{k} (1 \leq k \leq n) .$

Hãy chứng minh các công thức trên.

Gợi ý: Sử dụng công thức $C_{n}^{k} = \frac{n!}{k! (n - k)!}, n \in ℕ, 0 \leq k \leq n .$

Lời giải:

+) Có $C_{n}^{k} = \frac{n!}{k! (n - k)!}, C_{n}^{n - k} = \frac{n!}{(n - k)! [n - (n - k)]!} = \frac{n!}{(n - k)! k!} = \frac{n!}{k! (n - k)!} .$

Vậy $C_{n}^{k} = C_{n}^{n - k} .$

+) $C_{n}^{k - 1} + C_{n}^{k} = \frac{n!}{(k - 1)! (n - k + 1)!} + \frac{n!}{k! (n - k)!}$

$= \frac{\frac{(n + 1)!}{n + 1}}{\frac{k!}{k} (n - k + 1)!} + \frac{\frac{(n + 1)!}{n + 1}}{k! \frac{(n - k + 1)!}{(n - k + 1)}} = \frac{k}{n + 1} . \frac{(n + 1)!}{k! (n - k + 1)!} + \frac{n - k + 1}{n + 1} . \frac{(n + 1)!}{k! (n - k + 1)!}$

$= \frac{k}{n + 1} . \frac{(n + 1)!}{k! [(n + 1) - k]!} + \frac{n - k + 1}{n + 1} . \frac{(n + 1)!}{k! [(n + 1) - k]!}$

$= \frac{k}{n + 1} . C_{n + 1}^{k} + \frac{n - k + 1}{n + 1} . C_{n + 1}^{k} = (\frac{k}{n + 1} + \frac{n - k + 1}{n + 1}) C_{n + 1}^{k}$

$= \frac{k + (n - k + 1)}{n + 1} C_{n + 1}^{k} = \frac{n + 1}{n + 1} C_{n + 1}^{k} = C_{n + 1}^{k} .$

Xem thêm các bài giải Chuyên đề Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Khám phá 1 trang 34 Chuyên đề Toán 10: Có ba hộp, mỗi hộp đựng hai quả cầu được dán nhãn a và b (xem Hình 1)

Thực hành 1 trang 35 Chuyên đề Toán 10: Hãy khai triển:

Thực hành 2 trang 37 Chuyên đề Toán 10: Sử dụng tam giác Pascal, hãy khai triển:

Thực hành 3 trang 38 Chuyên đề Toán 10: Xác định hệ số của x² trong khai triển (3x + 2)⁹

Thực hành 4 trang 38 Chuyên đề Toán 10: Biết rằng trong khai triển (x + a)⁶ với a là một số thực, hệ số của x⁴ là 60. Tìm giá trị của a.

Thực hành 5 trang 38 Chuyên đề Toán 10: Chứng minh rằng, với mọi n∈ ℕ*, ta có

Vận dụng trang 38 Chuyên đề Toán 10: Trong hộp A có 10 quả cầu được đánh số từ 1 đến 10. Người ta lấy một số quả cầu từ hộp A rồi cho vào hộp B. Có tất cả bao nhiêu cách lấy, tính cả trường hợp lấy không quả (tức không lấy quả nào)?

Bài 1 trang 39 Chuyên đề Toán 10: Khai triển biểu thức:

Bài 2 trang 39 Chuyên đề Toán 10: Tìm hệ số của x¹⁰ trong khai triển của biểu thức (2 – x)¹²

Bài 3 trang 39 Chuyên đề Toán 10: Biết rằng a là một số thực khác 0 và trong khai triển của (ax + 1)⁶, hệ số của x⁴ gấp bốn lần hệ số của x². Tìm giá trị của a

Bài 4 trang 39 Chuyên đề Toán 10: Biết rằng hệ số của x² trong khai triển của (1 + 3x)ⁿ là 90. Tìm giá trị của n.

Bài 5 trang 39 Chuyên đề Toán 10: Chứng minh công thức nhị thức Newton (công thức (1), trang 35 ) bằng phương pháp quy nạp toán học.

Bài 6 trang 39 Chuyên đề Toán 10: Biết rằng (3x – 1)⁷ = a₀ + a₁x + a₂x² + a₃x³ + a₄x⁴ + a₅x⁵ + a₆x⁶ + a₇x⁷.

Bài 7 trang 39 Chuyên đề Toán 10: Một tập hợp có 12 phần tử thì có tất cả bao nhiêu tập hợp con?

Bài 8 trang 39 Chuyên đề Toán 10: Từ 15 bút chì màu có màu khác nhau đôi một,

Xem thêm các bài giải Chuyên đề Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Phương pháp quy nạp toán học

Bài tập cuối chuyên đề 2

Bài 5: Elip

Bài 6: Hypebol

Bài 7: Parabol

Từ khóa :

Giải bài tập Toán 10

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

48

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

45

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

43

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

55

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.