Với giải Câu hỏi  trang  49 Toán 10 Tập 1 Chân trời sáng tạo chi tiết trong Bài 2: Hàm số bạc hai giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem: 

Toán 10 Chân trời sáng tạo trang 57 Bài 2: Hàm số bậc hai

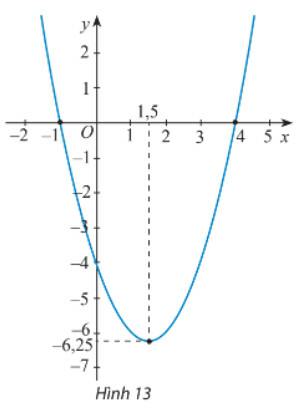
Bài 8 trang 57 Toán 10 Tập 1: Tìm công thức của hàm số bậc hai có đồ thị như Hình 13.

Phương pháp giải 

Gọi công thức của hàm số bậc hai là $y=a{x}^2+bx+c$

Đồ thị hàm số đi qua 3 điểm có tọa độ (-1;0), (4;0), (0;-4)

Lời giải 

Gọi công thức của hàm số bậc hai là $y=a{x}^2+bx+c$

Đồ thị hàm số đi qua 3 điểm có tọa độ (-1;0), (4;0), (0;-4)

$\begin{array}{l}\Rightarrow \{\begin{array}{l}a.(-1{)}^2+b.(-1)+c=0\\ a{.4}^2+b.4+c=0\\ a{.0}^2+b.0+c=-4\end{array}\iff \{\begin{array}{l}a-b+c=0\\ 16a+4b+c=0\\ c=-4\end{array}\iff \{\begin{array}{l}a-b=4\\ 16a+4b=4\\ c=-4\end{array}\\ \iff a=1,b=-3,c=-4.\end{array}$

Vậy hàm số cần tìm có công thức $y=x^2-3x-4$

Bài 9 trang 57 Toán 10 Tập 1: Chiếc cầu dây văng một nhịp được thiết kế hai bên thành cầu có dạng parabol và được cố định bằng các dây cáp song song.

Dựa vào bản vẽ ở Hình 14, hãy tính chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên. Biết:

-  Dây dài nhất là 5 m, dây ngắn nhất là 0,8 m. Khoảng cách giữa các dây bằng nhau.

-  Nhịp cầu dài 30 m.

-  Cần tính thêm 5% chiều dài mỗi sợi dây cáp để neo cố định.

Phương pháp giải 

Gắn hệ trục tọa độ, gọi công thức của hàm số có đồ thị là thành cầu.

Xác định hàm số và xác định tung độ của điểm có hoành độ là hình chiếu của các dây cáp dọc.

Lời giải 

Gọi $y=a{x}^2+bx+c$ là công thức của hàm số có đồ thị là thành cầu. 

Chọn hệ trục tọa độ Oxy như hình dưới:

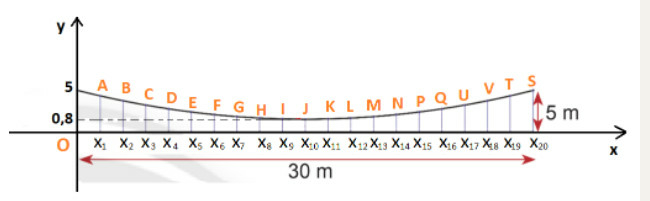
Khi đó độ dài dây cáp dọc ở mỗi mặt bên là tung độ của điểm biểu diễn tương ứng.

Ở mỗi mặt: có 21 dây cáp dọc, tương ứng cho 20 khoảng cách giữa chúng.

Khoảng cách giữa hai dây cáp liền kề là: $30:20=1,5\left(m\right)$

Khi đó: $x_0=0;x_1=1,5;x_2=3;x_3=4,5;...;x_n=1,5.n$

Dễ thấy: các điểm có tọa độ (0; 5), ($x_{10};0,8$), $(x_{20};5)$ thuộc đồ thị hàm số.

(Trong đó: $x_{10}=10.1,5=15;x_{20}=20.1,5=30.$)

Suy ra:

$f(0)=a{.0}^2+b.0+c=5\iff c=5$

Và $f(1)=a{.10}^2+b.10+c=0,8\iff 100a+10b+5=0,8$

$f(2)=a{.30}^2+b.30+c=5\iff 900a+30b+5=5$

Giải hệ phương trình $\{\begin{array}{l}100a+10b+5=0,8\\ 900a+30b+5=5\end{array}$ ta được $a=\frac{21}{1000};b=-\frac{63}{100}$

Như vậy $y=\frac{21}{1000}{x}^2-\frac{63}{100}x+5$

Gọi $y_0,y_1,y_2,..y_{20}$ là tung độ của các điểm có hoành độ lần lượt là $x_0,x_1,x_2,..x_{20}$

Ta có:

$\begin{array}{l}{y}_0=5\\ y_1=\frac{21}{1000}.1,5^2-\frac{63}{100}.1,5+5\\ y_2=\frac{21}{1000}.(2.1,5{)}^2-\frac{63}{100}.(2.1,5)+5=2^2.\frac{21}{1000}.1,5^2-2.\frac{63}{100}.1,5+5\\ ...\\ y_n=\frac{21}{1000}.(n.1,5{)}^2-\frac{63}{100}.(2.1,5)+5=n^2.\frac{21}{1000}.1,5^2-n.\frac{63}{100}.1,5+5\\ \Rightarrow T=y_0+y_1+y_2+..+y_{20}=5+\frac{21}{1000}.1,5^2.(1+2^2+...+{20}^2)-\frac{63}{100}.1,5.(1+2+...+20)+5.20\end{array}$

Mà $1+2^2+...+{20}^2=2870;1+2+...+20=210$

$\Rightarrow T=5+\frac{21}{1000}.1,5^2.2870-\frac{63}{100}.1,5.210+5.20\approx 42,16(m)$

Tổng chiều dài của các dây cáp dọc ở hai mặt bên là: $42,16.2=84,32(m)$

Vậy chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên là 84,32m.