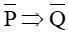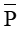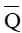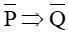Với giải Bài 1 trang 70 SBT Toán 10 Tập 2 Kết nối tri thức chi tiết trong Bài tập cuối năm giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Cho các mệnh đề: P: “Phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt”
Bài 1 trang 70 Sách bài tập Toán lớp 10 Tập 2: Cho các mệnh đề:
P: “Phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt”;
Q: “Phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0”.
a) Hãy phát biểu các mệnh đề: P ⇒ Q, Q ⇒ P, P ⇔ Q, 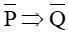 . Xét tính đúng sai của các mệnh đề này.
. Xét tính đúng sai của các mệnh đề này.
b) Dùng các khái niệm “điều kiện cần” và “điều kiện đủ” để diễn tả mệnh đề P ⇒ Q.
c) Gọi X là tập hợp các phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt, Y là tập hợp các phương trình bậc hai ax2 + bx + c = 0 có hệ số a và c trái dấu. Nêu mối quan hệ giữa hai tập hợp X và Y.
Lời giải:
a)
+ Mệnh đề P ⇒ Q: “Nếu phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt thì phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0”. Đây là mệnh đề đúng.
+ Mệnh đề Q ⇒ P: “ Nếu phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0 thì phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt”. Đây là mệnh đề đúng.
+ Mệnh đề P ⇔ Q: “Phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt khi và chỉ khi phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0”. Do P ⇒ Q, Q ⇒ P đều là các mệnh đề đúng nên mệnh đề P ⇔ Q là mệnh đề đúng.
+ Mệnh đề 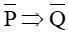
Mệnh đề 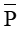 là mệnh đề phủ định của mệnh đề P và được phát biểu là: “Phương trình bậc hai ax2 + bx + c = 0 không có hai nghiệm phân biệt”.
là mệnh đề phủ định của mệnh đề P và được phát biểu là: “Phương trình bậc hai ax2 + bx + c = 0 không có hai nghiệm phân biệt”.
Mệnh đề 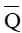 là mệnh đề phủ định của mệnh đề Q và được phát biểu là: “Phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac ≤ 0”.
là mệnh đề phủ định của mệnh đề Q và được phát biểu là: “Phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac ≤ 0”.
Khi đó, ta phát biểu mệnh đề 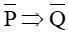 : “Nếu phương trình bậc hai ax2 + bx + c = 0 không có hai nghiệm phân biệt thì phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac ≤ 0”. Mệnh đề này là mệnh đề đúng.
: “Nếu phương trình bậc hai ax2 + bx + c = 0 không có hai nghiệm phân biệt thì phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac ≤ 0”. Mệnh đề này là mệnh đề đúng.
b)
+ Phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt là điều kiện đủ để phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0.
+ Phương trình bậc hai ax2 + bx + c = 0 có biệt thức ∆ = b2 – 4ac > 0 là điều kiện cần để phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt.
c) Ta có các phương trình bậc hai ax2 + bx + c = 0 có hệ số a và c trái dấu thì luôn có hai nghiệm trái dấu, hiển nhiên đây là hai nghiệm phân biệt. Nhưng các phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt thì hai nghiệm này chưa chắc đã trái dấu.
Do đó mọi phần tử của tập hợp Y thì đều là phần tử của tập hợp X.
Vậy Y là tập con của tập hợp X và ta viết Y ⊂ X.
Xem thêm các bài giải sách bài tập Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 1 trang 70 Sách bài tập Toán lớp 10 Tập 2: Cho các mệnh đề: P: “Phương trình bậc hai ax2 + bx + c = 0 có hai nghiệm phân biệt”...
Bài 2 trang 70 Sách bài tập Toán lớp 10 Tập 2: a) Biểu diễn hình học tập nghiệm D của hệ bất phương trình bậc nhất hai ẩn sau...
Bài 3 trang 70 Sách bài tập Toán lớp 10 Tập 2: Cho tam thức bậc hai f(x) = ax2 + bx + c với đồ thị là parabol có đỉnh I(1; 4) và đi qua điểm A(2; 3)...
Bài 4 trang 71 Sách bài tập Toán lớp 10 Tập 2: Một quả bóng chày được đánh đi với vận tốc 35 m/s hợp với phương ngang một góc bằng 45° ở độ cao 1 m so với mặt sân phẳng ở chỗ vụt bóng...
Bài 5 trang 71 Sách bài tập Toán lớp 10 Tập 2: Một công ty thời trang thấy rằng khi một loại áo phông được bán ở mức giá x (nghìn đồng) một chiếc thì số lượng áo phông bán được n cho bởi phương trình nhu cầu...
Bài 6 trang 71 Sách bài tập Toán lớp 10 Tập 2: Người ta ước tính rằng trong khoảng từ năm 2010 đến năm 2030, số lượng điện thoại di động bán được của một công ty...
Bài 7 trang 72 Sách bài tập Toán lớp 10 Tập 2: Tìm các giá trị của tham số m để hàm số y=√x2+2mx-2m+3 có tập xác định là toàn bộ tập số thực ℝ....
Bài 8 trang 72 Sách bài tập Toán lớp 10 Tập 2: Giải các phương trình chứa căn thức sau: a) √3x2-4x+1=√x2-x....
Bài 9 trang 72 Sách bài tập Toán lớp 10 Tập 2: Đội văn nghệ của một trường trung học phổ thông gồm có 5 học sinh khối lớp 10, 5 học sinh khối lớp 11 và 5 học sinh khối lớp 12...
Bài 10 trang 72 Sách bài tập Toán lớp 10 Tập 2: Viết khai triển nhị thức Newton của (3x – 2)n, biết n là số tự nhiên thoả mãn A2n+2C1n=30....
Bài 11 trang 72 Sách bài tập Toán lớp 10 Tập 2: Cho tam giác ABC có AB = 2, AC = 3, BC = 4...
Bài 12 trang 72 Sách bài tập Toán lớp 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3; 4), B(8; 6). Kẻ đường phân giác trong OD của tam giác OAB (D thuộc đoạn AB)...
Bài 13 trang 72 Sách bài tập Toán lớp 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có M, N, P lần lượt là trung điểm của các đoạn thẳng BC, AC, AB. Biết rằng M(1; 2), N(0; –1) và P(–2; 3)...
Bài 14 trang 72 Sách bài tập Toán lớp 10 Tập 2: Cho đường thẳng ∆: 3x + 4y – 25 = 0. Gọi (C) là đường tròn tâm O và tiếp xúc với ∆...
Bài 15 trang 73 Sách bài tập Toán lớp 10 Tập 2: Chuyển động của một vật thể trong khoảng thời gian 180 phút được thể hiện trong mặt phẳng toạ độ...
Bài 16 trang 73 Sách bài tập Toán lớp 10 Tập 2: Bảng sau đây cho biết lượng mưa trung bình hằng tháng tại Đà Nẵng và Hà Nội (mm)...
Bài 17 trang 73 Sách bài tập Toán lớp 10 Tập 2: Khi tham gia một trò chơi quay số trúng thưởng, mỗi người chơi chọn một số 4 chữ số (có tính cả số 0 ở đầu)...
Bài 18 trang 73 Sách bài tập Toán lớp 10 Tập 2: Khi tham gia một trò chơi bốc thăm trúng thưởng, mỗi người chơi chọn một bộ 6 số đôi một khác nhau từ 45 số: 1; 2;....; 45...,