Toán 10 Chân trời sáng tạo trang 97 Bài 3: Tích của một số với một vecto

Giang Ngày: 10-02-2023 Lớp 10

335

Với giải Câu hỏi trang 97 Toán 10 Tập 1 Chân trời sáng tạo trong Bài 3: Toichs của một số với một vecto giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Toán 10 Chân trời sáng tạo trang 97 Bài 3: Tích của một số với một vecto

Bài 1 trang 97 Toán 10 Tập 1: Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:

a) $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$

b) $\vec{A B} + \vec{A C} + \vec{A D} = 2 \vec{A C}$

Phương pháp giải

a) Sử dụng quy tắc ba điểm $\vec{M A} = \vec{M O} + \vec{O A}$ và tính chất trung điểm $\vec{O A} + \vec{O C} = \vec{0}$

b) Sử dụng tính chất của bình bình hành $\vec{A B} + \vec{A D} = \vec{A C}$

Lời giải

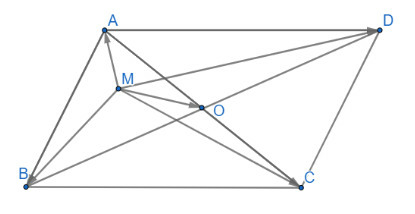
Bài 1 trang 97 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

a) $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$

$\Leftrightarrow \vec{M O} + \vec{O A} + \vec{M O} + \vec{O B} + \vec{M O} + \vec{O C} + \vec{M O} + \vec{O D} = 4 \vec{M O}$

$\Leftrightarrow 4 \vec{M O} + (\vec{O A} + \vec{O B}) + (\vec{O C} + \vec{O D}) = 4 \vec{M O}$

$\Leftrightarrow 4 \vec{M O} + \vec{0} + \vec{0} = 4 \vec{M O} \Leftrightarrow 4 \vec{M O} = 4 \vec{M O}$ (luôn đúng)

(vì O là giao điểm 2 đường chéo nên là trung điểm của AB, CD)

b) ABCD là hình bình hành nên ta có $\vec{A B} + \vec{A D} = \vec{A C}$

Suy ra $\vec{A B} + \vec{A C} + \vec{A D} = (\vec{A B} + \vec{A D}) + \vec{A C} = \vec{A C} + \vec{A C} = 2 \vec{A C}$ (đpcm)

Bài 2 trang 97 Toán 10 Tập 1: Cho tứ giác ABCD gọi M và N lần lượt là trung điểm của các cạnh AB và CD . Chứng minh rằng

a) $\vec{A C} + \vec{B D} = 2 \vec{M N}$

b) $\vec{A C} + \vec{B D} = \vec{B C} + \vec{A D}$

Phương pháp giải

Chèn điểm M: $\vec{A B} = \vec{A M} + \vec{M B}$ ,

Tính chất trung điểm $\vec{M A} + \vec{M B} = \vec{0}$

Lời giải

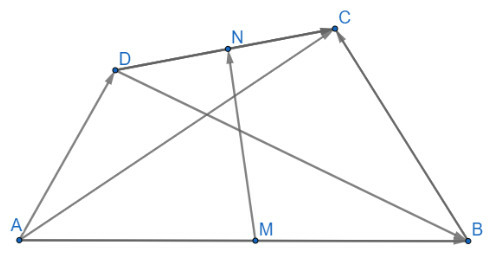
Bài 2 trang 97 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

a) $\vec{A C} + \vec{B D} = \vec{A M} + \vec{M N} + \vec{N C} + \vec{B M} + \vec{M N} + \vec{N D} = (\vec{A M} + \vec{B M}) + (\vec{M N} + \vec{M N}) + (\vec{N C} + \vec{N D}) = \vec{0} + 2 \vec{M N} + \vec{0} = 2 \vec{M N}$ (đpcm)

b) $\vec{A C} + \vec{B D} = \vec{B C} + \vec{A D}$

$\vec{B C} + \vec{A D} = \vec{B M} + \vec{M N} + \vec{N C} + \vec{A M} + \vec{M N} + \vec{N D}$

$(\vec{B M} + \vec{A M}) + (\vec{M N} + \vec{M N}) + (\vec{N C} + \vec{N D}) = 2 \vec{M N}$

Mặt khác ta có: $\vec{A C} + \vec{B D} = 2 \vec{M N}$

Suy ra $\vec{A C} + \vec{B D} = \vec{B C} + \vec{A D}$

Cách 2:

$\begin{array}{l} \vec{A C} + \vec{B D} = \vec{B C} + \vec{A D} \\ \Leftrightarrow \vec{A C} - \vec{A D} = \vec{B C} - \vec{B D} \\ \Leftrightarrow \vec{D C} = \vec{D C} (đ p c m) \end{array}$

Bài 3 trang 97 Toán 10 Tập 1: Cho hai điểm phân biệt A và B. Xác định điểm M sao cho

Phương pháp giải

Bước 1: Xác định hướng của hai vectơ

Bước 2: Xác định tỉ số độ dài $\frac{| \vec{M A} |}{| \vec{M B} |}$ $\vec{M A} + 4 \vec{M B} = \vec{0}$

Lời giải

Cách 1:

$\vec{M A} + 4 \vec{M B} = \vec{0} \Leftrightarrow \vec{M A} = - 4 \vec{M B} \Rightarrow \frac{M A}{M B} = \frac{| \vec{M A} |}{| \vec{M B} |} = \frac{| - 4 \vec{M B} |}{| \vec{M B} |} = 4$ và hai vectơ $\vec{M A}, \vec{M B}$ ngược hướng

Suy ra M nằm giữa AB sao cho $\frac{M A}{M B} = 4$

Cách 2:

$\begin{array}{l} \vec{M A} + 4 \vec{M B} = \vec{0} \\ \Leftrightarrow \vec{M B} + \vec{B A} + 4 \vec{M B} = \vec{0} \\ \Leftrightarrow 5 \vec{M B} = \vec{A B} \end{array}$

Vậy A, M, B thẳng hàng, M nằm giữa A và B sao cho $M B = \frac{1}{5} A B$

Bài 4 trang 97 Toán 10 Tập 1: Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm M tùy ý, chứng minh rằng $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M G}$

Phương pháp giải

Sử dụng quy tắc ba điểm $\vec{M A} = \vec{M O} + \vec{O A}$ và tính chất trung điểm

(với O là trung điểm của AB) $\vec{O A} + \vec{O B} = \vec{0}$

Lời giải

Bài 4 trang 97 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

$\begin{array}{l} \vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = (\vec{M G} + \vec{G E} + \vec{E A}) + (\vec{M G} + \vec{G E} + \vec{E B}) \\ + (\vec{M G} + \vec{G F} + \vec{F C}) + (\vec{M G} + \vec{G F} + \vec{F D}) \end{array}$

$= (\vec{M G} + \vec{M G} + \vec{M G} \vec{+ M G}) + 2 (\vec{G E} + \vec{G F}) + (\vec{E A} + \vec{E B}) + (\vec{F C} + \vec{F D})$

$= 4 \vec{M G} + 2. \vec{0} + \vec{0} + \vec{0} = 4 \vec{M G}$ (đpcm)

Bài 5 trang 97 Toán 10 Tập 1: Máy bay A đang bay về hướng Đông Bắc với tốc độ 600 km/h. Cùng lúc đó, máy bay B đang bay về hướng Tây Nam với tốc độ 800 km/h. Biểu diễn vectơ vận tốc $\vec{b}$ của máy bay B theo vectơ vận tốc $\vec{a}$ của máy bay A

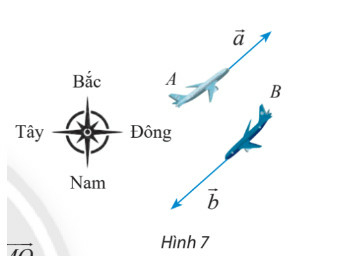
Bài 5 trang 97 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Lời giải

Vecto $\vec{a}, \vec{b}$ là vecto vận tốc của máy bay A và máy bay b.

Do đó $| \vec{a} |, | \vec{b} |$ lần lượt là độ lớn của vecto vận tốc tương ứng.

Ta có: $| \vec{a} | = 600, | \vec{b} | = 800$

$\Rightarrow \frac{| \vec{b} |}{| \vec{a} |} = \frac{800}{600} = \frac{4}{3}$

Hai hướng Đông Bắc và Tây Nam là ngược nhau, do đó $\vec{b} = - \frac{4}{3} \vec{a}$

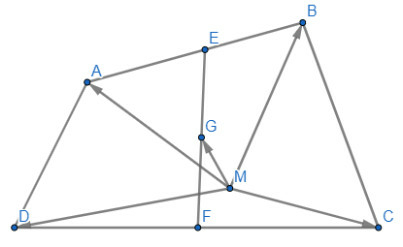
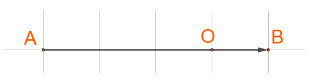
Bài 6 trang 97 Toán 10 Tập 1: Cho 2 điểm phân biệt A và B

a) Xác định điểm O sao cho $\vec{O A} + 3 \vec{O B} = \vec{0}$

b) Chứng minh rằng với mọi điểm M, ta có $\vec{M A} + 3 \vec{M B} = 4 \vec{M O}$

Phương pháp giải

a) Chèn điểm: $\vec{O A} = \vec{O B} + \vec{B A}$

Từ đó tìm $\vec{O B}$ theo $\vec{A B}$ đã biết

b) Chèn điểm O, làm xuất hiện $\vec{M O}$ ở vế trái.

Lời giải

a) $\vec{O A} + 3 \vec{O B} = \vec{0}$

$\begin{array}{l} \vec{O A} + 3 \vec{O B} = \vec{0} \\ \Leftrightarrow \vec{O B} + \vec{B A} + 3 \vec{O B} = \vec{0} \\ \Leftrightarrow \vec{O B} + 3 \vec{O B} = - \vec{B A} \\ \Leftrightarrow 4 \vec{O B} = \vec{A B} \\ \Leftrightarrow \vec{O B} = \frac{1}{4} \vec{A B} \end{array}$

Vậy O thuộc đoạn AB sao cho $O B = \frac{1}{4} A B$

Bài 6 trang 97 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

b) Ta có:

$\begin{array}{l} \vec{M A} + 3 \vec{M B} = (\vec{M O} + \vec{O A}) + 3 (\vec{M O} + \vec{O B}) \\ = (\vec{M O} + 3 \vec{M O}) + (\vec{O A} + 3 \vec{O B}) \\ = 4 \vec{M O} + \vec{0} = 4 \vec{M O} . (đ p c m) \end{array}$

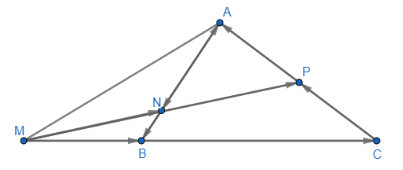
Bài 7 trang 97 Toán 10 Tập 1: Cho tam giác ABC

a) Xác định các điểm M, N, P thỏa mãn: $\vec{M B} = \frac{1}{2} \vec{B C}, \vec{A N} = 3 \vec{N B}, \vec{C P} = \vec{P A}$

b) Biểu thị mỗi vectơ $\vec{M N}, \vec{M P}$ theo hai vectơ $\vec{B C}, \vec{B A}$

c) Chứng minh ba điểm M, N, P thẳng hàng

Phương pháp giải

a) Xác định hướng và tỉ số độ dài

$\vec{M B} = k . \vec{B C} \Rightarrow \vec{M B}$ và $\vec{B C}$ cùng hướng; tỉ số độ dài $\frac{B C}{M B} = k$

b) Phân tích $\vec{M N}$ theo hai vecto $\vec{M B}, \vec{N B}$

c) $M, N, P$ thẳng hàng $\Leftrightarrow \vec{M N} = k . \vec{M P}$ $(k \in Z^{*})$

Lời giải chi tiết

a) Ta có:

+) $\vec{M B} = \frac{1}{2} \vec{B C} \Rightarrow \vec{M B}$ và $\vec{B C}$ cùng hướng; tỉ số độ dài $\frac{B C}{M B} = 2$

$\Rightarrow M$ nằm ngoài đoạn thẳng BC sao cho $M B = \frac{1}{2} B C$

+) $\vec{A N} = 3 \vec{N B} \Rightarrow \vec{A B} + \vec{B N} = 3 \vec{N B} \Rightarrow 4 \vec{N B} = \vec{A B} \Leftrightarrow \vec{N B} = \frac{1}{4} \vec{A B}$

$\Rightarrow N$ thuộc đoạn thẳng AB và $N B = \frac{1}{4} A B$

+) $\vec{C P} = \vec{P A} \Leftrightarrow \vec{P C} + \vec{P A} = \vec{0}$

$\Rightarrow P$ là trung điểm của CA

b) $\vec{M N} = \vec{M B} + \vec{B N} = \frac{1}{2} \vec{B C} + \frac{1}{4} \vec{B A}$

$\begin{array}{l} \vec{M P} = \vec{M C} + \vec{C P} = \vec{M C} + \frac{1}{2} \vec{C A} \\ = \frac{3}{2} \vec{B C} + \frac{1}{2} (\vec{B A} - \vec{B C}) \\ = \vec{B C} + \frac{1}{2} \vec{B A} \end{array}$