Với giải Câu hỏi trang 61 Toán 10 Tập 2 Chân trời sáng tạo trong Bài 3: Đường tròn trong mặt phẳng toạ độ học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem: 

Toán 10 Chân trời sáng tạo trang 61 Bài 3: Đường tròn trong mặt phẳng toạ độ

Thực hành 2 trang 61 Toán 10 Tập 2: Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm tọa độ tâm và bán kính của đường tròn đó

a) $x^2+y^2-2x-4y-20=0$

b) ${\left(x+5\right)}^2+{\left(y+1\right)}^2=121$

c) $x^2+y^2-4x-8y+5=0$

d) $2x^2+2y^2+6x+8y-2=0$

Phương pháp giải:

+) Phương trình có dạng ${\left(x-a\right)}^2+{\left(y-b\right)}^2=R^2$là đường tròn với tâm $I(a;b)$ và bán kính R

+) Phương trình $x^2+y^2-2ax-2by+c=0$ là phương trình đường tròn khi và chỉ khi $a^2+b^2-c>0$, khi đó nó có tâm I(a;b) và bán kính $R=\sqrt{a^2+b^2-c}$

Lời giải 

a) Phương trình đã cho có dạng $x^2+y^2-2ax-2by+c=0$ với $a=1,b=2,c=-20$

Ta có $a^2+b^2-c=1+4+20=25>0$. Vậy đây là phương trình đường tròn có tâm là $I(1;2)$ và có bán kính $R=\sqrt{25}=5$

b) Phương trình ${\left(x+5\right)}^2+{\left(y+1\right)}^2=121$ là phương trình dường tròn với tâm $I(-5;-1)$ và bán kinh $R=\sqrt{121}=11$

c) Phương trình đã cho có dạng $x^2+y^2-2ax-2by+c=0$ với $a=-3,b=-2,c=-2$

Ta có $a^2+b^2-c=9+4+2=15>0$. Vậy đây là phương trình đường tròn có tâm là $I(-3;-2)$ và có bán kính $R=\sqrt{15}$

d) Phương trình không có dạng $x^2+y^2-2ax-2by+c=0$ nên phương trình đã cho không là phương trình đường tròn.

Vận dụng 1 trang 61 Toán 10 Tập 2: Theo dữ kiện đã cho trong hoạt động khởi động của bài học, viết phương trình đường tròn biểu diễn tập hợp các điểm xa nhất mà vòi nước có thể phun tới

Phương pháp giải:

Tập hợp các điểm xa nhất tạo thành đường tròn với tâm I (a; b) và bán kính R

Phương trình là: ${\left(x-a\right)}^2+{\left(y-b\right)}^2=R^2$

Lời giải 

Theo giả thiết ta có: tâm $I(30;40)$ và bán kính $R=50$

Vậy phương trình tập hợp các điểm xa nhất mà vòi nước có thể phun tới là:

${\left(x-30\right)}^2+{\left(y-40\right)}^2={50}^2$

Vận dụng 2 trang 61 Toán 10 Tập 2: Một sân khấu đã được thiết lập một hệ trục tọa độ bởi đạo diễn có thể sắp đặt ánh sáng và xác định vị trí của các diễn viên. Cho biết một đèn chiếu đang gọi trên sân khấu một vùng sáng bên trong đường tròn (C) có phương trình ${\left(x-13\right)}^2+{\left(y-4\right)}^2=16$

a) Tìm tọa độ tâm và bán kính của đường tròn (C)

b) Cho biết tọa độ trên sân khấu của 3 diễn viên A, B, C  như sau: $A(11;4).B(8;5),C(15;5)$.Diễn viên nào đang được đèn chiếu sáng?

Phương pháp giải:

a) Với phương trình thì tâm là ${\left(x-a\right)}^2+{\left(y-b\right)}^2=R^2$thì tâm là $I(a;b)$ và bán kính R

b)         Bước 1: Tính khoảng cách của các diễn viên đến tâm vùng sáng

Bước 2: So sánh khoảng cách vừa tìm được với bán kính

+) Nếu nhỏ hơn hoặc bằng bán kính thì được chiếu sáng

+) Nếu lớn hơn bán kính thì không được chiếu sáng

Lời giải 

a) (C) có phương trình ${\left(x-13\right)}^2+{\left(y-4\right)}^2=16$nên có tâm là $I(13;4)$ và bán kính $R=\sqrt{16}=4$

 b) Ta có:$IA=\sqrt{{\left(11-13\right)}^2+{\left(4-4\right)}^2}=2,IB=\sqrt{{\left(8-13\right)}^2+{\left(5-4\right)}^2}=\sqrt{26}$

$IC=\sqrt{{\left(15-13\right)}^2+{\left(5-4\right)}^2}=\sqrt{5}$

$2<4\Rightarrow IA<R$, suy ra diễn viên A được chiếu sáng

$\sqrt{26}>4\Rightarrow IB>R$, suy ra diễn viên B không được chiếu sáng

$\sqrt{5}<4\Rightarrow IC<R$, suy ra diễn viên C được chiếu sáng

Vậy diễn viên A và C được chiếu sáng.

2. Phương trình tiếp tuyến của đường tròn

HĐ Khám phá 2 trang 61 Toán 10 Tập 2: Cho điểm $M_0\left(x_0;y_0\right)$ nằm trên đường tròn $(C)$ tâm $I(a;b)$và cho điểm$M(x;y)$ tùy ý trong mặt phẳng Oxy. Gọi $\mathrm{\Delta }$ là tiếp tuyến với $(C)$ tại $M_0$

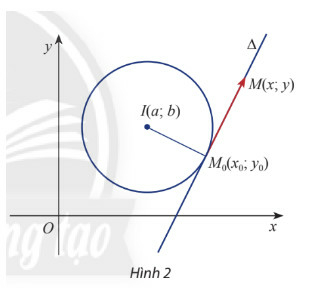
a) Viết biểu thức tọa độ của hai vt $\overrightarrow{M_{0}M}$ và $\overrightarrow{M_{0}I}$

b) Viết biểu thức tọa độ  của tích vô hướng của hai vt $\overrightarrow{M_{0}M}$ và $\overrightarrow{M_{0}I}$

c) Phương trình $\overrightarrow{M_{0}M}.\overrightarrow{M_{0}I}=0$là phương trình của đường thẳng nào?

Phương pháp giải:

a) Với $A(a;b),B(x;y)$ thì tọa độ của vt $\overrightarrow{AB}=(x-a;y-b)$

b) Với $\overrightarrow{a}=\left(a,b\right),\overrightarrow{b}=(x;y)$ thì $\overrightarrow{a}.\overrightarrow{b}=ax+by$

c) Từ tích vô hướng đưa ra kết luận là $\overrightarrow{M_{0}M}=\left(x-x_0;y-y_0\right)$, $\overrightarrow{M_{0}I}=\left(a-x_0;b-y_0\right)$

Lời giải 

a) Biểu thức tọa độ của hai vt $\overrightarrow{M_{0}M}$ và $\overrightarrow{M_{0}I}$ là $\overrightarrow{M_{0}M}=\left(x-x_0;y-y_0\right)$, $\overrightarrow{M_{0}I}=\left(a-x_0;b-y_0\right)$

b) Ta có:

$\overrightarrow{M_{0}M}.\overrightarrow{M_{0}I}=\left(x-x_0\right)\left(a-x_0\right)+\left(b-y_0\right)\left(y-y_0\right)$

c) $\overrightarrow{M_{0}M}.\overrightarrow{M_{0}I}=0\Rightarrow \overrightarrow{M_{0}M}\mathrm{\perp }\overrightarrow{M_{0}I}$

Mà $M_{0}I$ là đoạn thẳng nối tâm với điểm nằm ngoài

Vậy ta thấy pt đường thẳng $M{M}_0$ là tiếp tuyến của đường tròn tại điểm $M_0$.