Toán 10 Kết nối tri thức trang 58 Bài 9: Tích của một vecto với một số

Giang Ngày: 12-02-2023 Lớp 10

384

Với giải Câu hỏi trang 58 Toán 10 Tập 1 Kết nối tri thức trong 9: Tích của một vecto với một số học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Toán 10 Kết nối tri thức trang 58 Bài 9: Tích của một vecto với một số

Bài 4.11 trang 58 Toán lớp 10: Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Hãy biểu thị $\vec{A M}$ theo hai vecto $\vec{A B}$ và $\vec{A D}$ .

Phương pháp giải:

Bước 1: Phân tích vecto $\vec{A M}$ theo hai vecto cạnh.

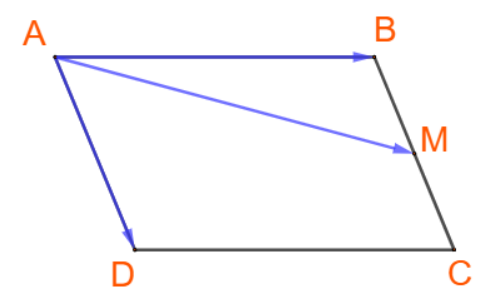
Bài 4.11 trang 58 Toán lớp 10 Tập 1 I Kết nối tri thức với cuộc sống (ảnh 2)

Bước 2: Biểu thị hai vecto cạnh theo vecto $\vec{A B}$ , $\vec{A D}$ .

Lời giải:

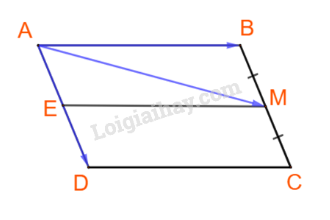
Bài 4.11 trang 58 Toán lớp 10 Tập 1 I Kết nối tri thức với cuộc sống (ảnh 1)

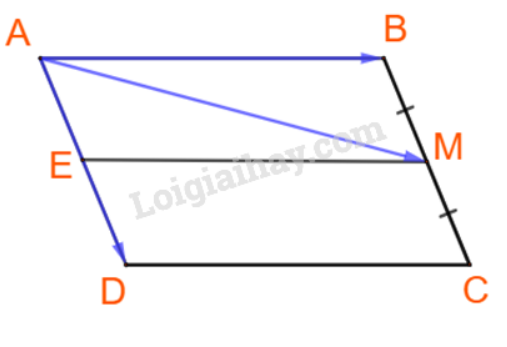
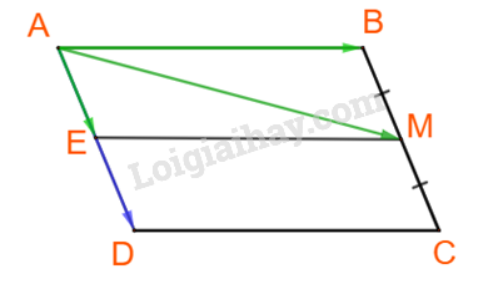
Từ M kẻ đường thẳng song song với AB, cắt AD tại E.

Khi đó tứ giác ABME là hình bình hành.

Do đó: $\vec{A M} = \vec{A B} + \vec{A E}$ .

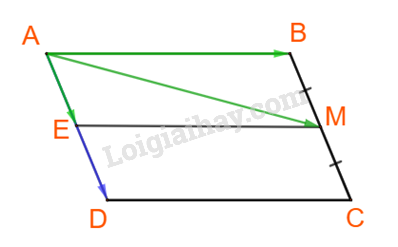
Dễ thấy: $A E = B M = \frac{1}{2} B C = \frac{1}{2} A D$

$\Rightarrow \vec{A E} = \frac{1}{2} \vec{A D}$

$\Rightarrow \vec{A M} = \vec{A B} + \frac{1}{2} \vec{A D}$

Vậy $\vec{A M} = \vec{A B} + \frac{1}{2} \vec{A D}$

Chú ý: +) Dựng hình hình hành sao cho đường chéo là vecto cần biểu thị, 2 cạnh của nó song song với giá của hai vecto đang biểu thị theo.

Bài 4.12 trang 58 Toán lớp 10: Cho tứ giác ABCD. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh $\vec{B C} + \vec{A D} = 2 \vec{M N} = \vec{A C} + \vec{B D} .$

Phương pháp giải:

+ Với ba điểm A, B, C bất kì ta luôn có: $\vec{A B} + \vec{B C} = \vec{A C}$

+ M là trung điểm của đoạn AB thì $\vec{M A} + \vec{M B} = \vec{0} = \vec{A M} + \vec{B M}$

Lời giải:

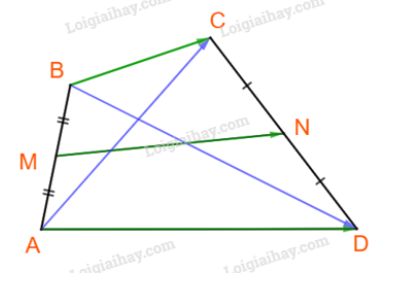
Bài 4.12 trang 58 Toán lớp 10 Tập 1 I Kết nối tri thức với cuộc sống (ảnh 1)

Ta có:

$\vec{M N} = \vec{M A} + \vec{A D} + \vec{D N}$

Mặt khác: $\vec{M N} = \vec{M B} + \vec{B C} + \vec{C N}$

$\begin{array}{l} \Rightarrow 2 \vec{M N} = \vec{M A} + \vec{A D} + \vec{D N} + \vec{M B} + \vec{B C} + \vec{C N} \\ \Leftrightarrow 2 \vec{M N} = (\vec{M A} + \vec{M B}) + (\vec{D N} + \vec{C N}) + \vec{B C} + \vec{A D} \\ \Leftrightarrow 2 \vec{M N} = \vec{0} + \vec{0} + \vec{B C} + \vec{A D} \\ \Leftrightarrow 2 \vec{M N} = \vec{B C} + \vec{A D} \end{array}$

Tương tự ta cũng có:

${\begin{cases} \vec{M N} = \vec{M A} + \vec{A C} + \vec{C N} \\ \vec{M N} = \vec{M B} + \vec{B D} + \vec{D N} \end{cases}$

$\begin{array}{l} \Rightarrow 2 \vec{M N} = \vec{M A} + \vec{A C} + \vec{C N} + \vec{M B} + \vec{B D} + \vec{D N} \\ \Leftrightarrow 2 \vec{M N} = (\vec{M A} + \vec{M B}) + (\vec{C N} + \vec{D N}) + \vec{A C} + \vec{B D} \\ \Leftrightarrow 2 \vec{M N} = \vec{0} + \vec{0} + \vec{A C} + \vec{B D} \\ \Leftrightarrow 2 \vec{M N} = \vec{A C} + \vec{B D} \end{array}$

Vậy $\vec{B C} + \vec{A D} = 2 \vec{M N} = \vec{A C} + \vec{B D} .$

Bài 4.13 trang 58 Toán lớp 10: Cho hai điểm phân biệt A và B.

a) Hãy xác định điểm K sao cho $\vec{K A} + 2 \vec{K B} = \vec{0}$ .

b) Chứng minh rằng với mọi điểm O, ta có $\vec{O K} = \frac{1}{3} \vec{O A} + \frac{2}{3} \vec{O B} .$

Phương pháp giải:

Nhắc lại: Với ba điểm A, B, C bất kì ta luôn có: $\vec{A B} + \vec{B C} = \vec{A C}$

a) Cách 1: Nhận xét về phương chiều, độ lớn của hai vecto $\vec{K A}$ và $\vec{K B}$ , suy ra vị trí điểm K.

Cách 2: Biểu diễn vecto $\vec{K A}$ hoặc $\vec{K B}$ ) theo vecto $\vec{A B}$ .

b) Biểu diễn vecto $\vec{O K}$ bằng cách chèn điểm: $\vec{O A} = \vec{O K} + \vec{K A}; \vec{O B} = \vec{O K} + \vec{K B} .$

Lời giải:

a) Cách 1:

Ta có: $\vec{K A} + 2 \vec{K B} = \vec{0}$ .

$\Leftrightarrow \vec{K A} = - 2 \vec{K B}$

Suy ra vecto $\vec{K A}$ và vecto $\vec{K B}$ cùng phương, ngược chiều và $K A = 2. K B$

$\Rightarrow K, A, B$ thẳng hàng, K nằm giữa A và B thỏa mãn: $K A = 2. K B$

Cách 2:

Ta có: $\vec{K A} + 2 \vec{K B} = \vec{0}$ .

$\begin{array}{l} \Leftrightarrow (\vec{K B} + \vec{B A}) + 2 \vec{K B} = \vec{0} \\ \Leftrightarrow 3. \vec{K B} + \vec{B A} = \vec{0} \\ \Leftrightarrow 3. \vec{K B} = \vec{A B} \\ \Leftrightarrow \vec{K B} = \frac{1}{3} \vec{A B} \end{array}$

Vậy K thuộc đoạn AB sao cho $K B = \frac{1}{3} A B$ .

b) Để $\vec{O K} = \frac{1}{3} \vec{O A} + \frac{2}{3} \vec{O B} .$

$\begin{array}{l} \Rightarrow \vec{O K} = \frac{1}{3} (\vec{O K} + \vec{K A}) + \frac{2}{3} (\vec{O K} + \vec{K B}) \\ \Leftrightarrow \vec{O K} = (\frac{1}{3} \vec{O K} + \frac{2}{3} \vec{O K}) + (\frac{1}{3} \vec{K A} + \frac{2}{3} \vec{K B}) \\ \Leftrightarrow \vec{O K} = \vec{O K} + \frac{1}{3} (\vec{K A} + 2 \vec{K B}) \\ \Leftrightarrow \vec{O K} = \vec{O K} + \frac{1}{3} . \vec{0} \\ \Leftrightarrow \vec{O K} = \vec{O K} . \end{array}$

Hiển nhiên đúng với mọi điểm O.

Vậy với mọi điểm O, ta có $\vec{O K} = \frac{1}{3} \vec{O A} + \frac{2}{3} \vec{O B} .$

Chú ý: Với những biểu thức đơn giản (chỉ có 3 điểm) thì từ giải thiết ta có thể suy ra ngay phương, chiều, độ dài của chúng để xác định điểm M.

Với các biểu thức phức tạp hơn (có nhiều hơn 3 điểm) thì nên sử dụng phương pháp như trên: quy về một vecto chưa biết, được biểu diễn qua các vecto đã biết.

Bài 4.14 trang 58 Toán lớp 10: Cho tam giác ABC

a) Hãy xác định điểm M để $\vec{M A} + \vec{M B} + 2 \vec{M C} = \vec{0}$

b) Chứng minh rằng với mọi điểm O, ta có $\vec{O A} + \vec{O B} + 2 \vec{O C} = 4 \vec{O M}$

Phương pháp giải:

Với ba điểm A, B, C bất kì ta luôn có: $\vec{A B} + \vec{B C} = \vec{A C}$

Lời giải:

a) Ta có: $\vec{M A} + \vec{M B} + 2 \vec{M C} = \vec{0} \Leftrightarrow \vec{M A} + (\vec{M A} + \vec{A B}) + 2 (\vec{M A} + \vec{A C}) = \vec{0}$

$\begin{array}{l} \Leftrightarrow \vec{M A} + (\vec{M A} + \vec{A B}) + 2 (\vec{M A} + \vec{A C}) = \vec{0} \\ \Leftrightarrow 4 \vec{M A} + \vec{A B} + 2 \vec{A C} = \vec{0} \\ \Leftrightarrow 4 \vec{A M} = \vec{A B} + 2 \vec{A C} \\ \Leftrightarrow \vec{A M} = \frac{1}{4} \vec{A B} + \frac{1}{2} \vec{A C} \end{array}$

Trên cạnh AB, AC lấy điểm D, E sao cho $A D = \frac{1}{4} A B; A E = \frac{1}{2} A C$

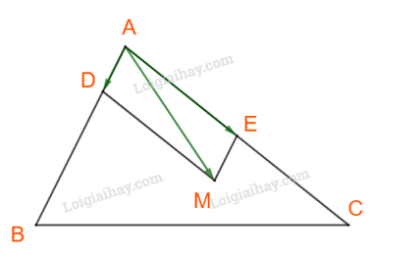
Bài 4.14 trang 58 Toán lớp 10 Tập 1 I Kết nối tri thức với cuộc sống (ảnh 2)

Khi đó $\vec{A M} = \vec{A D} + \vec{A E}$ hay M là đỉnh thứ tư của hình bình hành AEMD.

Cách 2:

Ta có: $\vec{M A} + \vec{M B} + 2 \vec{M C} = \vec{0} \Leftrightarrow (\vec{M C} + \vec{C A}) + (\vec{M C} + \vec{C B}) + 2 \vec{M C} = \vec{0}$

$\begin{array}{l} \Leftrightarrow 4 \vec{M C} + \vec{C A} + \vec{C B} = \vec{0} \\ \Leftrightarrow 4. \vec{C M} = \vec{C A} + \vec{C B} \end{array}$

Gọi D là đỉnh thứ tư của hình bình hành ACBD.

Khi đó: $\vec{C D} = \vec{C A} + \vec{C B}$ $\Rightarrow 4. \vec{C M} = \vec{C D}$

$\Leftrightarrow \vec{C M} = \frac{1}{4} \vec{C D} \Leftrightarrow \vec{C M} = \frac{1}{2} \vec{C O}$

Với O là tâm hình bình hành ACBD, cũng là trung điểm đoạn AB.

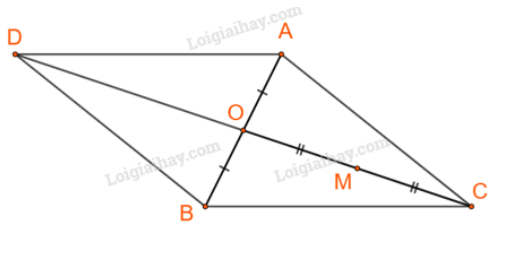
Bài 4.14 trang 58 Toán lớp 10 Tập 1 I Kết nối tri thức với cuộc sống (ảnh 1)

Vậy M là trung điểm của trung tuyến kẻ từ C của tam giác ABC.

b) Chứng minh rằng với mọi điểm O, ta có $\vec{O A} + \vec{O B} + 2 \vec{O C} = 4 \vec{O M}$

Với mọi điểm O, ta có: ${\begin{cases} \vec{O A} = \vec{O M} + \vec{M A}; \\ \vec{O B} = \vec{O M} + \vec{M B}; \\ \vec{O C} = \vec{O M} + \vec{M C} \end{cases}$

$\begin{array}{l} \Rightarrow \vec{O A} + \vec{O B} + 2 \vec{O C} = (\vec{O M} + \vec{M A}) + (\vec{O M} + \vec{M B}) + 2 (\vec{O M} + \vec{M C}) \\ = 4 \vec{O M} + (\vec{M A} + \vec{M B} + 2 \vec{M C}) = 4 \vec{O M} + \vec{0} = 4 \vec{O M} . \end{array}$