Với giải Câu hỏi trang 9 Toán 10 Tập 2 Kết nối tri thức trong Bài 15: Hàm số học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem: 

Toán 10 Kết nối tri thức trang 9 Bài 15: Hàm số

Luyện tập 3 trang 9 SGK Toán 10 Tập 2: Vẽ đồ thị của hàm số $y=3x+1$ và $y=-2x^2$. Hãy cho biết:

a) Hàm số $y=3x+1$đồng biến hay nghịch biến trên $\mathbb{R}$

b) Hàm số $y=-2x^2$đồng biến hay nghịch biến trên $(-\mathrm{\infty };0)$ và $(0;+\mathrm{\infty })$.

Phương pháp giải:

Quan sát đồ thị hàm số trên (a;b)

Hàm số đồng biến nếu đồ thị có dạng đi lên từ trái sang phải.

Hàm số nghịch biến nếu đồ thị có dạng đi xuống từ trái sang phải.

Lời giải:

Vẽ đồ thị $y=3x+1;y=-2x^2$

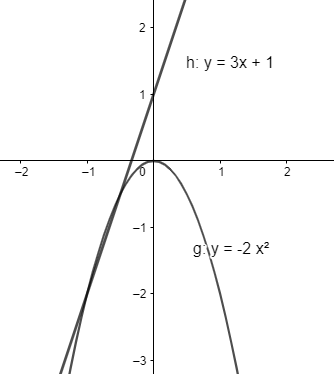
a) Trên $\mathbb{R}$, đồ thị $y=3x+1$ đi lên từ trái sang phải, như vậy hàm số $y=3x+1$ đồng biến trên $\mathbb{R}$

b) Trên khoảng $\left(-\mathrm{\infty };0\right)$, đồ thị $y=-2x^2$đi lên từ trái sang phải với mọi $x\in \left(-\mathrm{\infty };0\right)$ , như vậy hàm số đồng biến trên $\left(-\mathrm{\infty };0\right)$

Trên khoảng $\left(0;+\mathrm{\infty }\right)$, đồ thị $y=-2x^2$đi xuống từ trái sang phải với mọi $x\in \left(0;+\mathrm{\infty }\right)$ , như vậy hàm số nghịch biến trên $\left(0;+\mathrm{\infty }\right)$

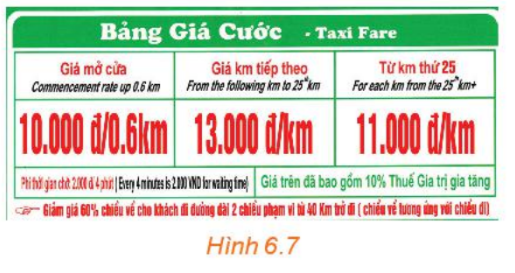
Vận dụng 2 trang 9 SGK Toán 10 Tập 2: Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7.

a) Tính số tiền phải trả khi di chuyển 25 km.                                

b) Lập công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển.

c) Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến trên khoảng nào.

Lời giải:

Gọi x là số km taxi đã đi; y (nghìn đồng) là số tiền cước phải trả

a) Khi di chuyển 25km thì

Với 0,6km đầu tiên, số tiền cước phải trả 10000 (đồng)

Với những km tiếp theo, số tiền cước phải trả 13000.(25-0,6)=317200(đồng)

Vậy số tiền cước phải trả 317200+10000=327200(đồng)

b) Khi hành khách đi từ 0km đến 0,6km thì $y=10$(nghìn đồng)

Khi hành khách đi từ 0,7km đến 25km thì $y=10+(x-0,6).13=13x+2,2$(nghìn đồng)

Khi khách hàng đi từ 25km trở lên $y=13.25+2,2+(x-25).11=11x+52,2$ (nghìn đồng)

c) Vẽ đồ thị hàm số

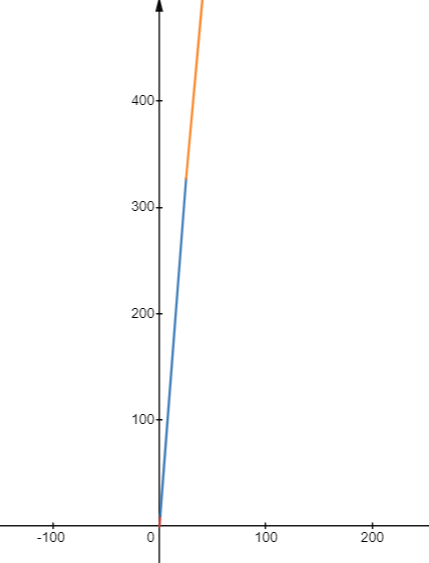
Nhìn trên đồ thị ta có thể thấy đồ thị đồng biến trên $\left(0;+\mathrm{\infty }\right)$

Bài tập

Bài 6.1 trang 9 SGK Toán 10 Tập 2: Xét hai đại lượng x, y phụ thuộc vào nhau theo các hệ thức dưới đây. Những trường hợp nào thì y là hàm số của x?

a) $x+y=1$

b) $y=x^2$

c) $y^2=x$            

d) $x^2-y^2=0$

Phương pháp giải:

Biểu diễn y theo x, nếu với mỗi giá trị của x ta chỉ tìm được duy nhất một giá trị y tương ứng thì y là hàm số của x.

Lời giải:

a) $x+y=1\Rightarrow y=1-x$, vậy với mỗi giá trị x chỉ có 1 giá trị y giá trị y, vậy x=y+1 là hàm số

b) $y=x^2$là 1 hàm số

c) $y^2=x\Rightarrow$$y=\sqrt{x}$hoặc $y=-\sqrt{x}$(nếu $x\ge 0$), vậy 1 giá trị của x lại có 2 giá trị y, nên đây không phải là hàm số

d) $x^2-y^2=0\iff x^2=y^2$, y=x hoặc y=-x, vậy 1 giá trị của x lại có 2 giá trị y, nên đây không phải là hàm số

Bài 6.2 trang 9 SGK Toán 10 Tập 2: Hãy cho một ví dụ về hàm số được cho bằng bảng hoặc biểu đồ. Hãy chỉ ra tập xác định và tập giá trị của hàm số đó.

Lời giải:

Ta có bảng sau:

Với mỗi giá trị của x ta có 1 giá trị của y, vậy bảng trên biểu thị cho 1 hàm số

Tập xác định của hàm số $D=\left\{-2;-1;-\frac{1}{2};0;\frac{1}{2};1;2\right\}$

Tập giá trị của hàm số $\left\{1;\frac{1}{2};\frac{1}{4};0;-\frac{1}{4};-\frac{1}{2};-1\right\}$

Bài 6.3 trang 9 SGK Toán 10 Tập 2: Tìm tập xác định của các hàm số sau:

a) $y=2x^3+3x+1$

b) $y=\frac{x-1}{x^2-3x+2}$

c) $y=\sqrt{x+1}+\sqrt{1-x}$

Lời giải:

a) Hàm $y=2x^3+3x+1$ là hàm đa thức nên có tập xác định $D=\mathbb{R}$

b) Biểu thức $\frac{x-1}{x^2-3x+2}$có nghĩa khi $x^2-3x+2\ne 0\iff x\ne 1$và $x\ne 2$

Vậy tập xác định của hàm số đã cho là $D=\mathbb{R}/\left\{1;2\right\}$

c) Biểu thức $\sqrt{x+1}+\sqrt{1-x}$ có nghĩa khi $x+1\ge 0$ và $1-x\ge 0$, tức là $-1\le x\le 1$

Vậy tập xác định của hàm số đã cho là $D=\left[-1;1\right]$

Bài 6.4 trang 9 SGK Toán 10 Tập 2: Tìm tập xác định và tập giá trị của mỗi hàm số sau:

a) $y=2x+3$   

b) $y=2x^2$

Lời giải:

a) Biểu thức $2x+3$ có nghĩa với mọi x, nên có tập xác định $D=\mathbb{R}$

Do đó tập giá trị của hàm số là $\mathbb{R}$

b) Biểu thức $2x^2$ có nghĩa với mọi x, nên có tập xác định $D=\mathbb{R}$

Ta có: $x^2\ge 0$ Do đó $y=2x^2\ge 0$, tập giá trị của hàm số là $\left[0;+\mathrm{\infty }\right)$

Bài 6.5 trang 9 SGK Toán 10 Tập 2: Vẽ đồ thị các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng.

a) $y=-2x+1$     

b)$y=-\frac{1}{2}{x}^2$

Phương pháp giải:

Vẽ hình, quan sát đồ thị hàm số trên (a;b)

Hàm số đồng biến nếu đồ thị có dạng đi lên từ trái sang phải.

Hàm số nghịch biến nếu đồ thị có dạng đi xuống từ trái sang phải.

Lời giải:

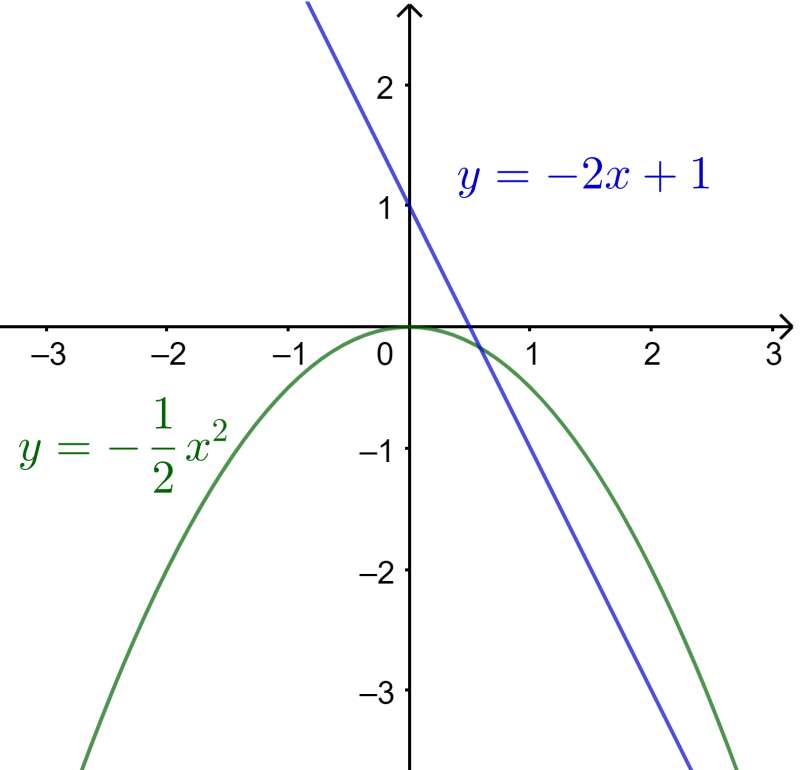
Nhìn vào đồ thị, ta thấy:

a) Hàm số $y=-2x+1$nghịch biến trên $\mathbb{R}$

b) Hàm số $y=-\frac{1}{2}{x}^2$ đồng biến trên khoảng $\left(-\mathrm{\infty };0\right)$; nghịch biến trên khoảng $\left(0;+\mathrm{\infty }\right)$

Bài 6.6 trang 9 SGK Toán 10 Tập 2: Giá thuê xe ô tô tự lái là 1,2 triệu đồng một ngày cho hai ngày đầu tiên và 900 nghìn đòng cho mỗi ngày tiếp theo. Tổng số tiền T phải trả là một hàm số của số ngày x mà khách thuê xe.

a) Viết công thức của hàm số $T=T(x)$

b) Tính T(2), T(3), T(5) và cho biết ý nghĩa của mỗi giá trị này.

Lời giải:

a)

Nếu $0<x\le 2$ thì $T(x)=1,2x$ (triệu đồng)

Nếu $x>2$ thì $T(x)=1,2.2+0,9.(x-2)=0,9x+0,6$ (triệu đồng)

Số tiền phải trả sau khi thuê x ngày là

$T(x)=\{\begin{array}{l}1,2x(0<x\le 2)\\ 0,9x+0,6(x>2)\end{array}$

b) $T(2)=1,2.2=2,4$  (triệu đồng)

Ý nghĩa: số tiền khách phải trả khi thuê 2 ngày là 2,4 triệu đồng

$T(3)=0,9.3+0,6=3,3$  (triệu đồng)

Ý nghĩa: số tiền khách phải trả khi thuê 3 ngày là 3,3 triệu đồng

$T(5)=0,9.5+0,6=5,1$

Ý nghĩa: số tiền khách phải trả khi thuê 5 ngày là 5,1 triệu đồng