Với giải Câu hỏi trang 23 Toán 10 Tập 2 Kết nối tri thức trong Bài 17: Dấu của tam thức bậc hai học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Kết nối tri thức trang 23 Bài 17: Dấu của tam thức bậc hai
Luyện tập 3 trang 23 SGK Toán 10 Tập 2: Giải các bất phương trình sau:
a) −5x2+x−1≤0
b) x2−8x+16≤0
c) x2−x+6>0
Phương pháp giải:
Để giải bất phương trình bậc hai, ta cần xét dấu tam thức f(x)=ax2+bx+x(a≠0)
từ đó suy ra tập nghiệm.
Xét dấu tam thức bậc hai f(x)=ax2+bx+c
Bước 1: Tính Δ=b2−4ac
Bước 2:
- Nếu Δ<0 thì f(x) luôn cùng dấu với a với mọi x∈R
- Nếu Δ=0 thì f(x)có nghiệm kép là x0 . Vậy f(x)cùng dấu với a với x≠x0
- Nếu Δ>0 thì f(x)có 2 nghiệm là x1;x2(x1<x2). Ta lập bảng xét dấu.

Lời giải:
a) Tam thức f(x)=−5x2+x−1 có Δ=−19<0, hệ số a=−5<0 nên f(x) luôn âm (cùng dấu với a) với mọi x, tức là −5x2+x−1<0 với mọi x∈R. Suy ra bất phương trình có vô số nghiệm
b) Tam thức g(x)=x2−8x+16 có Δ=0, hệ số a=1>0 nên g(x) luôn dương (cùng dấu với a) với mọi x≠4, tức là x2−8x+16>0 với mọi x≠4
Suy ra bất phương trình có nghiệm duy nhất là x=4
c) Tam thức h(x)=x2−x+6 có Δ=−23<0, hệ số a=1>0 nên h(x) luôn dương (cùng dấu với a) với mọi x, tức là x2−x+6>0 với mọi x∈R. Suy ra bất phương trình có vô số nghiệm
Vận dụng trang 23 SGK Toán 10 Tập 2: Độ cao so với mặt đất của một quá bóng được ném lên theo phương thẳng đứng được mô tả bởi hàm số bậc hai h(t)=−4,9t2+20t+1, ở độ cao h(t)tính bằng mét và thời gian t tình bằng giây. Trong khoảng thời điểm nào trong quá trình bay của nó, quả bóng sẽ ở độ cao trên 5m so với mặt đất.
Phương pháp giải:
Tìm khoảng thời gian t để h(t)>5, bài toán đưa về xét dấu tam thức f(t)=h(t)−5
Các bước xét dấu tam thức bậc hai f(t)=at2+bt+c
Bước 1: Tính Δ=b2−4ac
Bước 2:
- Nếu Δ<0 thì f(t) luôn cùng dấu với a với mọi t∈R
- Nếu Δ=0 thì f(t)có nghiệm kép là t0 . Vậy f(t)cùng dấu với a với t≠t0
- Nếu Δ>0 thì f(t)có 2 nghiệm là t1;t2(t1<t2). Ta lập bảng xét dấu.

Kết luận khoảng chứa t thỏa mãn f(t)>0
Lời giải:
Để quả bóng ở độ cao trên 5m so với mặt đất thì:
h(t)>5⇒−4,9t2+20t+1>5⇒−4,9t2+20t−4>0
Đặt f(t)=−4,9t2+20t−4có Δ′=b′2−ac=102−(−4,9).(−4)=80,4>0nên f(t)có 2 nghiệm: t1=−b′+√Δ′a=−10+√80,4−4,9=10−√80,44,9t2=−b′−√Δ′a=−10−√80,4−4,9=10+√80,44,9
Mặt khác a=−4,9<0, do đó ta có bảng xét dấu sau
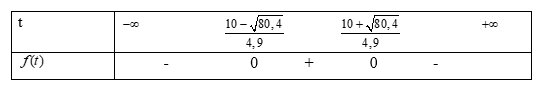
Do đó để h(t)>5thì t∈(10−√80,44,9;10+√80,44,9)
Vậy để quả bóng sẽ ở độ cao trên 5m so với mặt đất thì t∈(10−√80,44,9;10+√80,44,9)
Xem thêm các bài giải Toán 10 Kết nối tri thức hay, chi tiết khác:
HĐ1 trang 19 SGK Toán 10 Tập 2: Hãy chỉ ra một đặc điểm chung của các biểu thức dưới đây...
Luyện tập 1 trang 19 SGK Toán 10 Tập 2: Hãy cho biết biểu thức nào sau đây là tam thức bậc hai...
HĐ2 trang 19 SGK Toán 10 Tập 2: Cho hàm số bậc hai ...
HĐ3 trang 20 SGK Toán 10 Tập 2: Cho đồ thị hàm số như Hình 6.18...
Luyện tập 2 trang 22 SGK Toán 10 Tập 2: Xét dấu các tam thức bậc hai sau:...
Luyện tập 3 trang 23 SGK Toán 10 Tập 2: Giải các bất phương trình sau:...
Bài 6.15 trang 24 SGK Toán 10 Tập 2: Xét dấu các tam thức bậc hai sau:...
Bài 6.16 trang 24 SGK Toán 10 Tập 2: Giải các bất phương trình bậc hai:...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.