Với giải Câu hỏi trang 24 Toán 10 Tập 2 Kết nối tri thức trong Bài 17: Dấu của tam thức bậc hai học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Kết nối tri thức trang 24 Bài 17: Dấu của tam thức bậc hai
Bài 6.15 trang 24 SGK Toán 10 Tập 2: Xét dấu các tam thức bậc hai sau:
a)
b)
c)
d)
Phương pháp giải:
Xét dấu tam thức bậc hai
Bước 1: Tính
Bước 2:
- Nếu thì luôn cùng dấu với a với mọi
- Nếu thì có nghiệm kép là . Vậy cùng dấu với a với
- Nếu thì có 2 nghiệm là . Ta lập bảng xét dấu.

Lời giải:
a) có >0, và có hai nghiệm phân biệt . Do đó ta có bảng xét dấu :
Suy ra với mọi và với mọi

b) có và a=1>0 nên có nghiệm kép và với
c) có , <0 và có hai nghiệm phân biệt . Do đó ta có bảng xét dấu :

Suy ra với mọi và với mọi
d) có <0 và <0 nên với mọi
Bài 6.16 trang 24 SGK Toán 10 Tập 2: Giải các bất phương trình bậc hai:
a)
b)
c)
d)
Phương pháp giải:
Xét dấu tam thức bậc hai
Bước 1: Tính
Bước 2:
- Nếu thì luôn cùng dấu với a với mọi
- Nếu thì có nghiệm kép là . Vậy cùng dấu với a với
- Nếu thì có 2 nghiệm là . Ta lập bảng xét dấu.

Lời giải:
a) Tam thức có nên f(x) có 2 nghiệm phân biệt
Mặt khác a=1>0, do đó ta có bảng xét dấu:

Tập nghiệm của bất phương trình là
b) Tam thức có nên g(x) có 2 nghiệm phân biệt
Mặt khác a=1>0, do đó ta có bảng xét dấu:
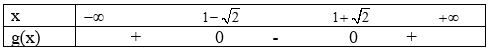
Tập nghiệm của bất phương trình là
c) Tam thức cónên h(x) có 2 nghiệm phân biệt
Mặt khác a=-3<0, do đó ta có bảng xét dấu:

d) Tam thức có , hệ số a=5>0 nên k(x) luôn dương ( cùng dấu với a) với mọi x, tức là với mọi . Suy ra bất phương trình có vô số nghiệm
Phương pháp giải:
Để tam thức bậc hai với mọi thì:
a>0 và
Lời giải:
Để tam thức bậc hai với mọi
Ta có: a=1>0 nên
Tam thức có nên f(x) có 2 nghiệm phân biệt
Mặt khác a=1>0, do đó ta có bảng xét dấu sau:

Bài 6.18 trang 24 SGK Toán 10 Tập 2: Một vật được ném theo phương thẳng đứng xuống dưới từ độ cao 320 m với vận tốc ban đầu . Hỏi sau ít nhất bao nhiêu giây, vật đó cách mặt đất không quá 100 m? Giả thiết rằng sức cản của không khí là không đáng kể
Phương pháp giải:
Tìm hàm tính độ cao so với mặt đất của vật ,
Tìm khoảng thời gian t để , bài toán đưa về xét dấu tam thức
Bước 1: Tính
Bước 2:
- Nếu thì luôn cùng dấu với a với mọi
- Nếu thì có nghiệm kép là . Vậy cùng dấu với a với
- Nếu thì có 2 nghiệm là . Ta lập bảng xét dấu.

Kết luận khoảng chứa t thỏa mãn
Lời giải:
Quãng đường vật rơi được sau t(s) là:
Để vật cách mặt đất không quá 100m thì
Tam thức có nên f(t) có 2 nghiệm phân biệt (t>0)
Mặt khác a=1>0 nên ta có bảng xét dấu:

Do t>0 nên
Vậy sau ít nhất khoảng 5 thì vật đó cách mặt đất không quá 100m
Bài 6.19 trang 24 SGK Toán 10 Tập 2: Xét đường tròn đường kính AB=4 và một điểm M di chuyển trên đoạn AB, đặt AM=x (H.6.19). Xét hai đường tròn đường kính AM và MB. Kí hiệu S(x) là diện tích phần hình phằng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ. Xác định các giá trị của x để diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ
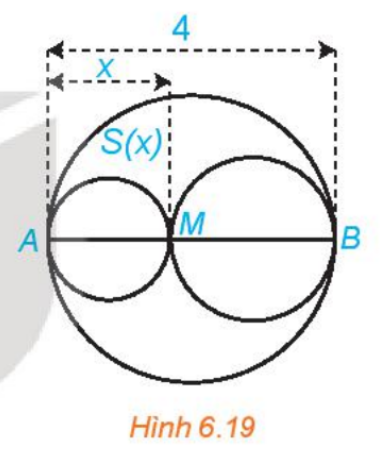
Phương pháp giải:
Bước 1: Tính diện tích hình tròn đường kính AB, AM, MB theo x
Bước 2: Tính diện tích phần hình phằng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ theo x
Bước 3: Lập bất phương trình từ dữ kiện bài toán
Lời giải:
Ta có: AM
Diện tích hình tròn đường kính AB là
Diện tích hình tròn đường kính AM là
Diện tích hình tròn đường kính MB là
Diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ là
Vì diện tich S(x) không vượt quá 1 nửa tổng diện tích hai hình tròn nhỏ nên:
Khi đó :
Xét tam thức có nên f(x) có 2 nghiệm phân biệt
Mặt khác a=3>0, do đó ta có bảng xét dấu:
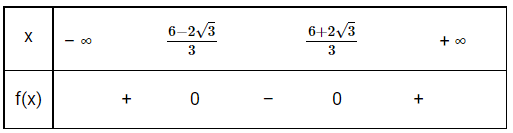
Do đó với mọi
Mà 0<x<4 nên
Xem thêm các bài giải Toán 10 Kết nối tri thức hay, chi tiết khác:
HĐ1 trang 19 SGK Toán 10 Tập 2: Hãy chỉ ra một đặc điểm chung của các biểu thức dưới đây...
Luyện tập 1 trang 19 SGK Toán 10 Tập 2: Hãy cho biết biểu thức nào sau đây là tam thức bậc hai...
HĐ2 trang 19 SGK Toán 10 Tập 2: Cho hàm số bậc hai ...
HĐ3 trang 20 SGK Toán 10 Tập 2: Cho đồ thị hàm số như Hình 6.18...
Luyện tập 2 trang 22 SGK Toán 10 Tập 2: Xét dấu các tam thức bậc hai sau:...
Luyện tập 3 trang 23 SGK Toán 10 Tập 2: Giải các bất phương trình sau:...
Bài 6.15 trang 24 SGK Toán 10 Tập 2: Xét dấu các tam thức bậc hai sau:...
Bài 6.16 trang 24 SGK Toán 10 Tập 2: Giải các bất phương trình bậc hai:...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.