Với giải Câu hỏi trang 80 SBT Toán 10 Tập 1 Chân trời sáng tạo trong Bài tập cuối chương 4 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập SBT Toán 10. Mời các bạn đón xem: 

SBT Toán 10 Chân trời sáng tạo trang 80: Bài tập cuối chương 4

Bài 1 trang 80 SBT Toán 10: Khẳng định nào sau đây là đúng?

A. $\sin \alpha =\sin \left({180}^{\circ }-\alpha \right)$   

B. $\cos \alpha =\cos \left({180}^{\circ }-\alpha \right)$

C. $\tan \alpha =\tan \left({180}^{\circ }-\alpha \right)$   

D. $\cot \alpha =\cot \left({180}^{\circ }-\alpha \right)$

Lời giải:

$\sin \alpha =\sin \left({180}^{\circ }-\alpha \right)$ 

$\cos \alpha =-\cos \left({180}^{\circ }-\alpha \right)$ 

Chọn A. $\sin \alpha =\sin \left({180}^{\circ }-\alpha \right)$

Bài 2 trang 80 SBT Toán 10: Trong các khẳng định sau đây, khẳng định nào sai?

A. $\cos {45}^{\circ }=\sin {45}^{\circ }$   

B. $\cos {45}^{\circ }=\sin {135}^{\circ }$

C. $\cos {30}^{\circ }=\sin {120}^{\circ }$   

D. $\sin {60}^{\circ }=\cos {120}^{\circ }$

Lời giải:

$\cos {45}^{\circ }=\sin \left({90}^{\circ }-{45}^{\circ }\right)=\sin {45}^{\circ }=\sin \left({180}^{\circ }-{45}^{\circ }\right)=\sin {135}^{\circ }$

=> A, B đúng

$\cos {30}^{\circ }=\sin \left({90}^{\circ }-{30}^{\circ }\right)=\sin {60}^{\circ }=\sin \left({180}^{\circ }-{60}^{\circ }\right)=\sin {120}^{\circ }$, suy ra C đúng

Chọn D.

Bài 3 trang 80 SBT Toán 10: Bất đẳng thức nào sau đây là bất đẳng thức đúng?

A. $\sin {90}^{\circ }<\sin {150}^{\circ }$

B. $\sin {90}^{\circ }{15}^{\prime }<\sin {90}^{\circ }{30}^{\prime }$

C. $\sin {90}^{\circ }{30}^{\prime }>\cos {100}^{\circ }$ 

D. $\cos {150}^{\circ }>\cos {120}^{\circ }$

Lời giải:

$\sin {90}^{\circ }<\sin {150}^{\circ }\iff \sin {90}^{\circ }-\sin {150}^{\circ }<0$

Sử dụng máy tính cầm tay: $\sin {90}^{\circ }-\sin {150}^{\circ }$ ta được kết quả là $\frac{1}{2}>0$ => A sai

Tương tự ta có: $\sin {90}^{\circ }{15}^{\prime }-\sin {90}^{\circ }{30}^{\prime }=0,000029>0$=> B sai

$\sin {90}^{\circ }{30}^{\prime }-\cos {100}^{\circ }=1,17>0$ => C đúng

Chọn C

Bài 4 trang 80 SBT Toán 10: Trong các đẳng thức sau đây đẳng thức nào đúng?

A. $\sin {150}^{\circ }=-\frac{\sqrt{3}}{2}$   

B. $\cos {150}^{\circ }=\frac{\sqrt{3}}{2}$

C. $\tan {150}^{\circ }=-\frac{1}{\sqrt{3}}$

D. $\cot {150}^{\circ }=\sqrt{3}$

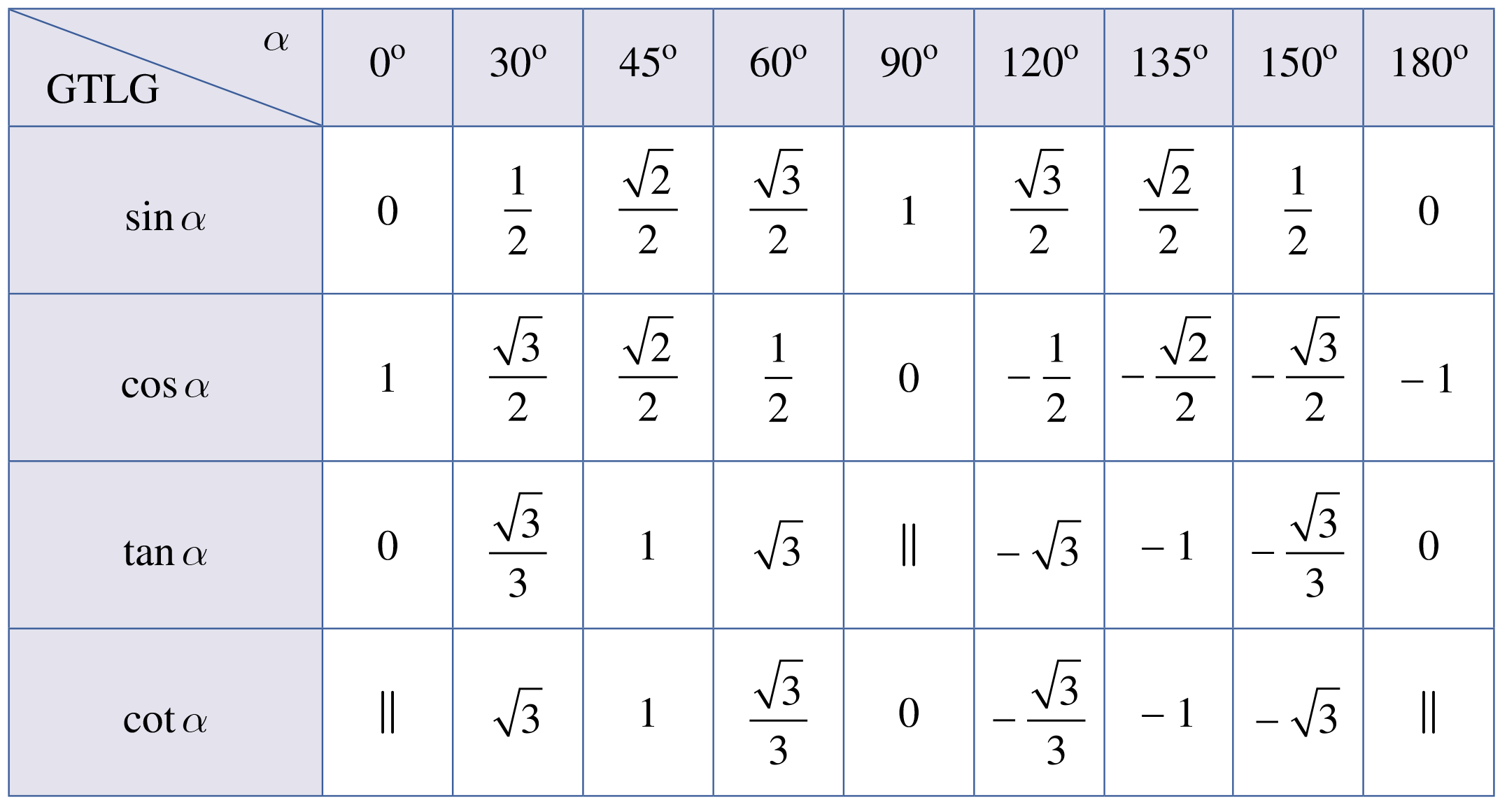
Lời giải:

Tra bảng giá trị lượng giác một số góc đặc biệt ta có $\tan {150}^{\circ }=-\frac{1}{\sqrt{3}}$

Chọn C. 

Bài 5 trang 80 SBT Toán 10: Cho tam giác ABC có $BC=a,CA=b,AB=c$. Mệnh đề nào sau đây đúng?

A. Nếu $b^2+c^2-a^2>0$ thì góc A nhọn

B. Nếu $b^2+c^2-a^2>0$ thì góc A tù

C. Nếu $b^2+c^2-a^2<0$ thì góc A nhọn

D. Nếu $b^2+c^2-a^2<0$ thì góc A vuông

Lời giải:

Áp dụng định lí côsin ta có: $\cos A=\frac{b^2+c^2-a^2}{2bc}$

Mà $a,b,c>0\Rightarrow 2bc>0$

Nên dấu của $\cos A$ phụ thuộc vào tử số $b^2+c^2-a^2$

Ta có $\begin{array}{l}{0}^{\circ }<\hat{A}<{90}^{\circ }\Rightarrow \cos A>0\\ {90}^{\circ }<\hat{A}<{180}^{\circ }\Rightarrow \cos A<0\\ \hat{A}={90}^{\circ }\Rightarrow \cos A=0\\ \hat{A}={180}^{\circ }\Rightarrow \cos A=-1\end{array}$

=>  Nếu $b^2+c^2-a^2>0$ thì góc A nhọn

Chọn A.

Bài 6 trang 80 SBT Toán 10: Cho tam giác ABC có $AB=4$ cm, $BC=7$ cm, $CA=9$. Giá trị $\cos A$ là

A. $\frac{2}{3}$ 

B. $\frac{1}{3}$

C. $\frac{4}{5}$ 

D. $\frac{8}{9}$

Lời giải:

Áp dụng định lí côsin ta có:

$\cos A=\frac{b^2+c^2-a^2}{2bc}=\frac{9^2+4^2-7^2}{\mathrm{2.9.4}}=\frac{2}{3}$

Chọn A

Bài 7 trang 80 SBT Toán 10: Cho tam giác ABC có $AB=8$ cm, $AC=18$ cm và có diện tích bằng 64 cm2. Giá trị $\sin A$ là:

A. $\frac{\sqrt{3}}{2}$ 

B. $\frac{3}{8}$ 

C. $\frac{4}{5}$   

D. $\frac{8}{9}$

Lời giải:

Áp dụng định lí sin ta có:

$S_{ABC}=\frac{1}{2}AB.AC.\sin A\Rightarrow \sin A=\frac{2S_{ABC}}{AB.AC}=\frac{2.64}{8.18}=\frac{8}{9}$

Chọn D

Bài 8 trang 80 SBT Toán 10: Cho tam giác ABC vuông cân tại A có $AB=AC=30$ cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích của tam giác GFC là:

A. 50 $c{m}^2$    

B. $50\sqrt{2}$ $c{m}^2$

C. 75 $c{m}^2$

D.$15\sqrt{105}$ $c{m}^2$

Lời giải:

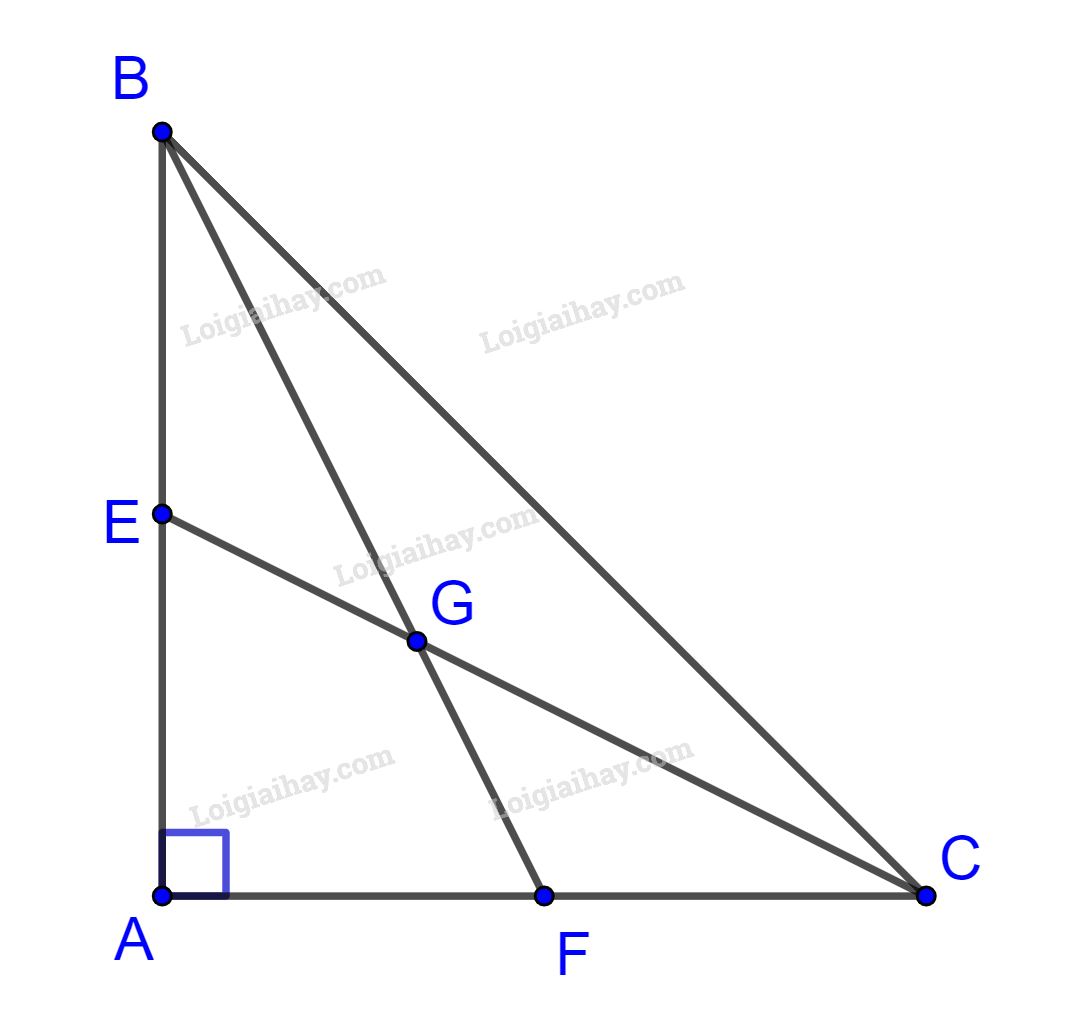
Ta có CE, BF  là đường trung tuyến nên G là trọng tâm của tam giác ABC.

$\Rightarrow GF=\frac{1}{3}BF\Rightarrow S_{\mathrm{\Delta }GCF}=\frac{1}{3}{S}_{\mathrm{\Delta }BCF}$

Mà $CF=\frac{1}{2}AC\Rightarrow S_{\mathrm{\Delta }BCF}=\frac{1}{2}{S}_{\mathrm{\Delta }ABC}$

$\Rightarrow S_{\mathrm{\Delta }GCF}=\frac{1}{6}{S}_{\mathrm{\Delta }ABC}=\frac{1}{6}.\frac{1}{2}.30.30=75\left(c{m}^2\right)$

Chọn C

Bài 9 trang 80 SBT Toán 10: Tam giác ABC có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:

A. 2S  

B. 3S 

C. 4S   

D. 6S

Lời giải:

Trước khi tăng ta có diện tích tam giác $S_{ABC}=\frac{1}{2}BC.CA.\sin C$

Sau khi tăng ta có: $B^{\prime }C=2BC,C{A}^{\prime }=3CA$, suy ra diện tích tam giác sau khi tăng là

                   $S_{A^{\prime }{B}^{\prime }C}=\frac{1}{2}{B}^{\prime }C.A^{\prime }C\sin C=\frac{1}{2}.2BC.3CA.\sin C=6S_{ABC}$

Chọn D