Với giải Câu hỏi trang 79 SBT Toán 10 Tập 2 Chân trời sáng tạo trong Bài tập cuối chương 9 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập SBT Toán 10. Mời các bạn đón xem:
SBT Toán 10 Chân trời sáng tạo trang 79: Bài tập cuối chương 9
Bài 4 trang 79 SBT Toán 10: Tính bán kính của đường tròn tâm và tiếp xúc với đường thẳng
Phương pháp giải:
+
Lời giải:
Đường tròn tâm (I) tiếp xúc với d thì có bán kính bằng khoảng cách từ I đến d.
Bài 5 trang 79 SBT Toán 10:Tính khoảng cách giữa hai đường thẳng và (biết )
Lời giải:
Khoảng cách giữa hai đường thẳng và (khi ) là khoảng cách từ M bất kì (thuộc ) đến
Gọi
Bài 6 trang 79 SBT Toán 10: Tìm tâm và bán kính của các đường tròn trong các trường hợp sau:
a)
b)
c)
Phương pháp giải:
Phương trình: là phương trình đường tròn khi: khi đó
Lời giải:
a)
b)
c)
+ Phương trình đã cho có các hệ số
+ Tính , nên phương trình của đường tròn có tâm và bán kính
Bài 7 trang 79 SBT Toán 10: Lập phương trình đường tròn trong các trường hợp sau:
a) Có tâm và bán kính bằng 7
b) Có tâm và đi qua điểm
c) Đi qua hai điểm và có tâm nằm trên đường thẳng
d) Đi qua gốc tọa độ và cắt hai trục tọa độ tại các điểm có hoành độ là 8, tung độ là 6
Phương pháp giải:
Phương trình đường tròn có tâm và bán kính R
Lời giải:
a) Có tâm và bán kính bằng 7
+ Phương trình đường tròn
b) Có tâm và đi qua điểm
+ Bán kính
+ Phương trình đường tròn
c) Đi qua hai điểm và có tâm nằm trên đường thẳng
+ Gọi I là tâm đường tròn,
+
+ Phương trình đường tròn
d) Đi qua gốc tọa độ và cắt hai trục tọa độ tại các điểm có hoành độ là 8, tung độ là 6
+ Gọi tâm đường tròn là , hai điểm A(8;0), B(0;6) là giao của đường tròn với 2 trục tọa độ.
Ta có:
Khi đó
Phương trình đường tròn
Bài 8 trang 79 SBT Toán 10: Viết phương trình tiếp tuyến với đường tròn tại điểm
Phương pháp giải:
Phương trình tiếp tuyến của tại có vectơ pháp tuyến là
Lời giải:
+
+ Phương trình tiếp tuyến d của tại có vectơ pháp tuyến là
Bài 9 trang 79 SBT Toán 10: Gọi tên các đường conic sau:
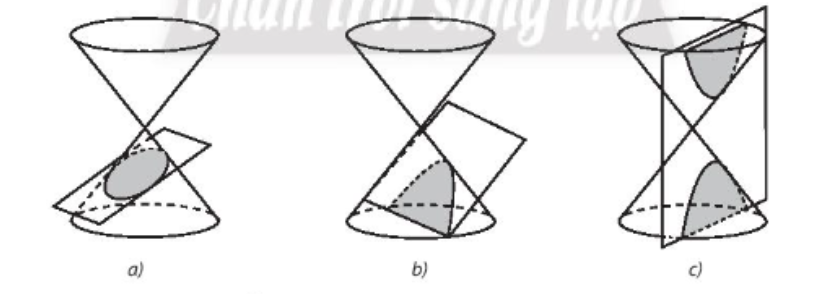
Lời giải:
a) Elip (đườn cong khép kín, không là đường tròn)
b) Parabol
c) Hypebol (gồm hai nhánh)
Bài 10 trang 79 SBT Toán 10: Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục lớn và trục nhỏ các elip sau:
a)
b)
Phương pháp giải:
Phương trình Elip có dạng với
+ hai tiêu điểm
+ Đỉnh:
+ Độ dài trục lớn 2a, độ dài trục nhỏ 2b
Lời giải:
a) Elip (E) có
+ Các tiêu điểm
+ Các đỉnh
+ Độ dài trục lớn , độ dài trục nhỏ
b) có
+ Các tiêu điểm
+ Các đỉnh
+ Độ dài trục lớn , độ dài trục nhỏ
Xem thêm các bài giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 77 SBT Toán 10: Cho hai vectơ và . Góc giữa hai vectơ và là...
Bài 2 trang 77 SBT Toán 10: Cho hai điểm M (1;-2) và N (-3;4). Khoảng cách giữa hai điểm M và N là...
Bài 3 trang 77 SBT Toán 10: Trong tam giác ABC có . Trong các phát biểu sau, phát biểu nào đúng.
Bài 4 trang 77 SBT Toán 10: Cho phương trình tham số của đường thẳng ....
Bài 5 trang 77 SBT Toán 10: Đường thẳng đi qua điểm và song song với đường thẳng ...
Bài 6 trang 77 SBT Toán 10: Bán kính của đường tròn tâm và tiếp xúc với đường thẳng...
Bài 7 trang 77 SBT Toán 10: Cho đường tròn . Trong các mệnh đề sau đây, phát biểu nào sai...
Bài 8 trang 78 SBT Toán 10: Phương trình tiếp tuyến tại điểm Với đường tròn ...
Bài 9 trang 78 SBT Toán 10: Phương trình chính tắc của elip có hai đỉnh là và hai tiêu điểm....
Bài 10 trang 78 SBT Toán 10: Phương trình chính tắc của hypebol có hai điểm....
Bài 11 trang 78 SBT Toán 10: Phương trình chính tắc của parabol có tiêu điểm là...
Bài 12 trang 78 SBT Toán 10: Elip với độ dài hai trục là 20 và 12 có phương trình chính tắc là...
Bài 1 trang 78 SBT Toán 10: Trong mặt phẳng , cho ba điểm ...
Bài 2 trang 78 SBT Toán 10: Tìm góc giữa hai đường thẳng và ...
Bài 3 trang 78 SBT Toán 10: Cho tam giác ABC với tọa độ ba đỉnh là ...
Bài 4 trang 79 SBT Toán 10: Tính bán kính của đường tròn tâm và tiếp xúc với đường thẳng..
Bài 5 trang 79 SBT Toán 10:Tính khoảng cách giữa hai đường thẳng và ..
Bài 6 trang 79 SBT Toán 10: Tìm tâm và bán kính của các đường tròn trong các trường hợp sau...
Bài 7 trang 79 SBT Toán 10: Lập phương trình đường tròn trong các trường hợp sau...
Bài 8 trang 79 SBT Toán 10: Viết phương trình tiếp tuyến với đường tròn tại điểm ...
Bài 9 trang 79 SBT Toán 10: Gọi tên các đường conic sau...
Bài 10 trang 79 SBT Toán 10: Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục lớn và trục nhỏ các elip sau...
Bài 11 trang 80 SBT Toán 10: Viết phương trình chính tắc của elip thỏa mãn các điều kiện sau...
Bài 13 trang 80 SBT Toán 10: Viết phương trình chính tắc của hypebol thỏa mãn các điều kiện sau...
Bài 14 trang 80 SBT Toán 10: Tìm tọa độ tiêu điểm, phương trình đường chuẩn của các parabol sau...
Bài 15 trang 80 SBT Toán 10: Viết phương trình chính tắc của parabol thỏa mãn các điều kiện...
Bài 16 trang 80 SBT Toán 10: Một nhà mái vòm có mặt cát hình nửa elip cao 6 m, rộng 16 m...
Bài 18 trang 80 SBT Toán 10: Gương phản chiếu của một đèn pha có mặt cắt là một parabol (P)...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.