Toptailieu.vn giới thiệu Giải bài tập Toán lớp 10 Bài 3: Khái niệm vecto | Cánh diều - sách Cánh Diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10 Tập 1. Mời các bạn đón xem:
Nội dung bài viết
Toán 10 Cánh Diều Bài 3: Khái niệm vecto
Đoạn thẳng AB có hướng được gọi là gì?
Lời giải:
Đoạn thẳng AB có hướng được gọi là vecto →AB.
I. Khái niệm vecto
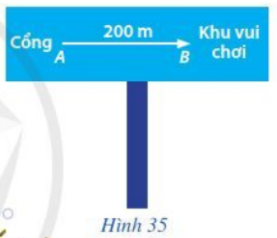
Lời giải:
Hình ảnh về mũi tên chỉ dẫn cho biết:
+) Hướng đi từ Cổng đến Khu vui chơi: Đi sang phải
+) Khoảng cách từ Cổng đến Khu vui chơi: 200 m.
Phương pháp giải:
Vectơ là một đoạn thẳng có hướng.
Xác định các đoạn thẳng (có hướng) mà điểm đầu và điểm cuối là A, B hoặc C.
Lời giải:
Các vectơ đó là: →AA,→AB,→AC,→BA,→BB,→CC,→CA,→CB,→CC.
Chú ý
+) vectơ →AB≠→BA(khác nhau về hướng)
+) →AA cũng là một vectơ.
II.Vecto cùng phương, vecto cùng hướng
Phương pháp giải:
+) Giá của vectơ là đường thẳng chứa vectơ ấy.
Lời giải:
Giá của vectơ →AB là đường thẳng AB
Giá của vectơ →CD là đường thẳng CD.
Giá của vectơ →PQ là đường thẳng PQ.
Dễ thấy: AB // CD và CD trùng PQ.
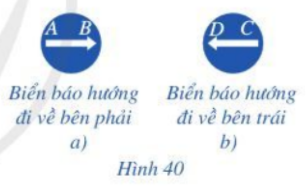
Phương pháp giải:
Bước 1: Nhận xét về giá của hai vectơ →AB và →CD, chỉ ra chúng cùng phương.
Bước 2: Nhận xét về hướng của hai vectơ và kết luận.
Lời giải:
Giá của vectơ →AB là đường thẳng AB
Giá của vectơ →CD là đường thẳng CD.
Dễ thấy: đường thẳng AB trùng với đường thẳng CD.
Do đó hai vectơ →AB và →CD có cùng phương.
Lại có: vectơ →AB chỉ hướng đi về bên phải còn vectơ →CD chỉ hướng đi về bên trái.
Vậy hai vectơ →AB và →CD có ngược hướng.
III. Hai vecto bằng nhau
Hoạt động 4 trang 80 Toán 10 Tập 1: Quan sát hai vectơ →AB và →CD ở hình 42.
a) Nhận xét về phương của hai vectơ đó.
b) Nhận xét về hướng của hai vectơ đó.
c) So sánh độ dài của hai vectơ đó.
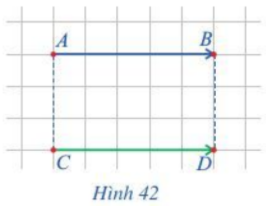
Phương pháp giải:
a) Nhận xét về giá của hai vectơ →AB và →CD, chỉ ra chúng cùng phương.
b) Nhận xét về hướng của hai vectơ đó (hướng sang phải/trái)
c) Độ dài của vectơ →AB là độ dài đoạn thẳng AB.
Lời giải:
a) Ta có:
Giá của vectơ →AB là đường thẳng AB
Giá của vectơ →CD là đường thẳng CD.
Dễ thấy: AB // CD do đó hai vectơ này cùng phương.
b) Quan sát hình 42, ta thấy cả hai vectơ →AB và →CD cùng hướng sang phải
Như vậy hai vectơ này cùng hướng.
c) Ta có: |→AB|=AB; |→CD|=CD và AB = CD (cùng dài 5 ô vuông)
Vậy độ dài của hai vectơ là bằng nhau.
Phương pháp giải:
Hai vectơ →AD,→BCbằng nhau nếu chúng cùng hướng và cùng độ dài.
Lời giải:
Ta có: →AD=→BC.
⇒{AD//BCAD=BC
Do đó tứ giác ABCD có một cặp cạnh đối song và bằng nhau
Vậy tứ giác ABCD là hình bình hành.
IV. Vecto không
V. Biểu thị một số đại lượng có hướng bằng vecto
Bài tập
Phương pháp giải:
Bước 1: Vẽ hình, xác định các vectơ trên.
Bước 2: Nhận xét về hướng của mỗi vectơ và kết luận.
Lời giải:
Do các vectơ đều nằm trên đường thẳng AB nên các vectơ này đều cùng phương với nhau.
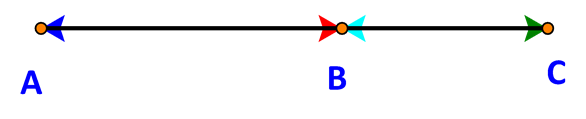
Dễ thấy:
Các vectơ →AB,→AC,→BC cùng hướng (từ trái sang phải.)
Các vectơ →BA,→CA,→CB cùng hướng (từ phải sang trái.)
Do đó, các cặp vectơ cùng hướng là:
→AB và →AC; →AC và →BC; →AB và →BC; →BA và →CA; →BA và →CB;→BA và →CB.
Các cặp vectơ ngược hướng là:
→AB và →BA; →AB và →CA; →AB và →CB;
→AC và →BA; →AC và →CA; →AC và →CB;
→BC và →BA; →BC và →CA; →BC và →CB;
Bài 2 trang 82 Toán 10 Tập 1: Cho đoạn thẳng MN có trung điểm là I.
a) Viết các vectơ khác vectơ-không có điểm đầu, điểm cuối là một trong ba điểm M, N, I.
b) vectơ nào bằng →MI? Bằng →NI?
Phương pháp giải:
a) Liệt kê các vectơ tạo thành từ 3 điểm M, N, I (điểm đầu và điểm cuối không trùng nhau)
b) Trong các vectơ ở câu a, vectơ nào: Cùng hướng, cùng độ dài với vectơ →MI (tương ứng là →NI).
Lời giải:

a) Các vectơ đó là: →MI,→IM,→IN,→NI,→MN,→NM.
b) Dễ thấy:
+) vectơ →INcùng hướng với vectơ →MI. Hơn nữa: |→IN|=IN=MI=|→MI|
⇒→IN=→MI
+) vectơ →IMcùng hướng với vectơ →NI. Hơn nữa: |→IM|=IM=NI=|→NI|
⇒→IM=→NI
Vậy →IN=→MI và →IM=→NI.
Bài 3 trang 82 Toán 10 Tập 1: Cho hình thang ABCD có hai đáy là AB và CD. Tìm vectơ:
a) Cùng hướng với →AB
b) Ngược hướng với →AB
Phương pháp giải:
Bước 1: Xác định giá của vectơ →AB. Liệt kê các vectơ cùng phương với →AB.
Bước 2: Chỉ ra vectơ cùng hướng, ngược hướng với →AB
Lời giải:
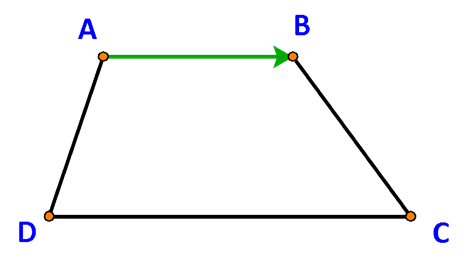
Giá của vectơ →AB là đường thẳng AB.
Các vectơ cùng phương với vectơ →AB là: →CD và →DC
a) vectơ →DC cùng hướng với vectơ →AB.
b) vectơ →CD ngược hướng với vectơ →AB.
Phương pháp giải:
+) Độ dài của vectơ →AB là độ dài đoạn thẳng AB.
Bước 1: Xác định độ dài của vectơ →AB,→AC.
Bước 2: Tính các cạnh đó dựa vào cạnh hình vuông.
Lời giải:
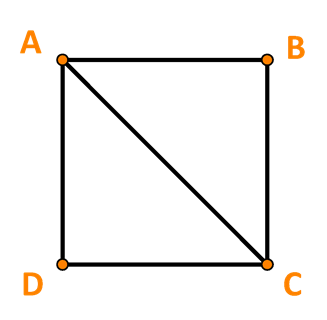
Ta có: |→AB|=AB và |→AC|=AC.
Mà AB=3,AC=3√2
⇒|→AB|=3;|→AC|=3√2
a) Hãy chỉ ra các cặp vectơ cùng phương.
b) Trong các cặp vectơ đó, cho biết chúng cùng hướng hay ngược hướng.
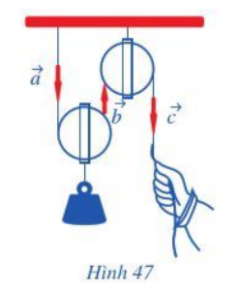
Phương pháp giải:
a)
Bước 1: Xác định giá của các vectơ →a,→b,→c. Từ đó suy ra các vectơ cùng phương.
Bước 2: Kết luận các cặp vectơ cùng phương.
b)
Nhận xét về hướng của 3 vectơ →a,→b,→c. Từ đó suy ra các cặp vectơ đó cùng hướng hay ngược hướng.
Lời giải:
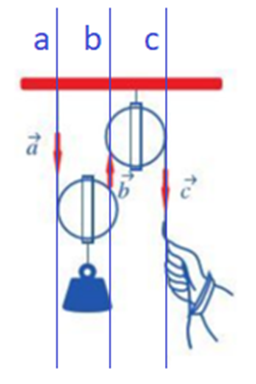
Gọi a, b, c là các đường thẳng lần lượt chứa các vectơ →a,→b,→c.
Khi đó: a, b, c lần lượt là giá của các vectơ →a,→b,→c
a) Dễ thấy: a // b // c
⇒ Ba vectơ →a,→b,→c cùng phương với nhau.
Vậy các cặp vectơ cùng phương là: →a và →b, →a và →c, →b và →c.
b) Quan sát ba vectơ, ta thấy: vectơ →a và →c cùng hướng xuống còn vectơ →b hướng lên trên.
Vậy vectơ →a và →c cùng hướng, vectơ →a và →c ngược hướng, vectơ →b và →c ngược hướng.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.