Toptailieu.vn giới thiệu Giải bài tập Toán lớp 10 Bài 2: Giải tam giác | Cánh diều - sách Cánh Diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10 Tập 1. Mời các bạn đón xem:
Toán 10 Cánh diều Bài 2: Giải tam giác
Câu hỏi khởi động trang 72 Toán 10 Tập 1: Từ xa xưa, con người đã cần đo đạc các khoảng cách mà không thể trực tiếp đo được. Chẳng hạn, để đo khoảng cách từ vị trí A trên bờ biển tới một hòn đảo (hay con tàu,...) trên biển, người xưa đã tìm ra một cách đo khoảng cách đó như sau:
Từ vị trí A, đo góc nghiêng so với bờ biển tới một vị trí C quan sát được trên đảo. Sau đó di chuyển dọc bờ biển đến vị trí B cách A một khoảng d và tiếp tục đo góc nghiêng so với bờ biển tới vị trí C đã chọn (Hình 18).
Bằng cách giải tam giác ABC,họ tính được khoảng cách AC.
Giải tam giác được hiểu như thế nào?
Lời giải:
Giải tam giác là việc đi tìm một số yếu tố của tam giác khi đã biết các yếu tố khác của tam giác đó.
Trong trường hợp này, giải tam giác ABC được hiểu là tìm cạnh AC khi biết cạnh AB, góc A và góc B.
Áp dụng định lí sin ta có:
Mà
I. Tính cách cạnh và góc của tam giác dựa trên một số điều kiện cho trước
Hoạt động 1 trang 72 Toán 10 Tập 1: Cho tam giác ABC có . Viết công thức tính BC theo
Phương pháp giải:
Áp dụng định lí cosin trong tam giác ABC:
Lời giải:
Áp dụng định lí cosin trong tam giác ABC ta có:
Hoạt động 2 trang 72 Toán 10 Tập 1: Cho tam giác ABC có . Viết công thức tính cos A.
Phương pháp giải:
Áp dụng định lí cosin cho tam giác ABC, từ đó suy ra công thức tính cos A.
Lời giải:
Áp dụng định lí cosin trong tam giác ABC ta có:
Chú ý
Tương tự, ta suy ra công thức tính như sau:
Hoạt động 3 trang 73 Toán 10 Tập 1: Viết công thức định lí sin cho tam giác ABC.
Lời giải:
Áp dụng định lí sin trong tam giác ABC ta có:
II. Tính diện tích tam giác
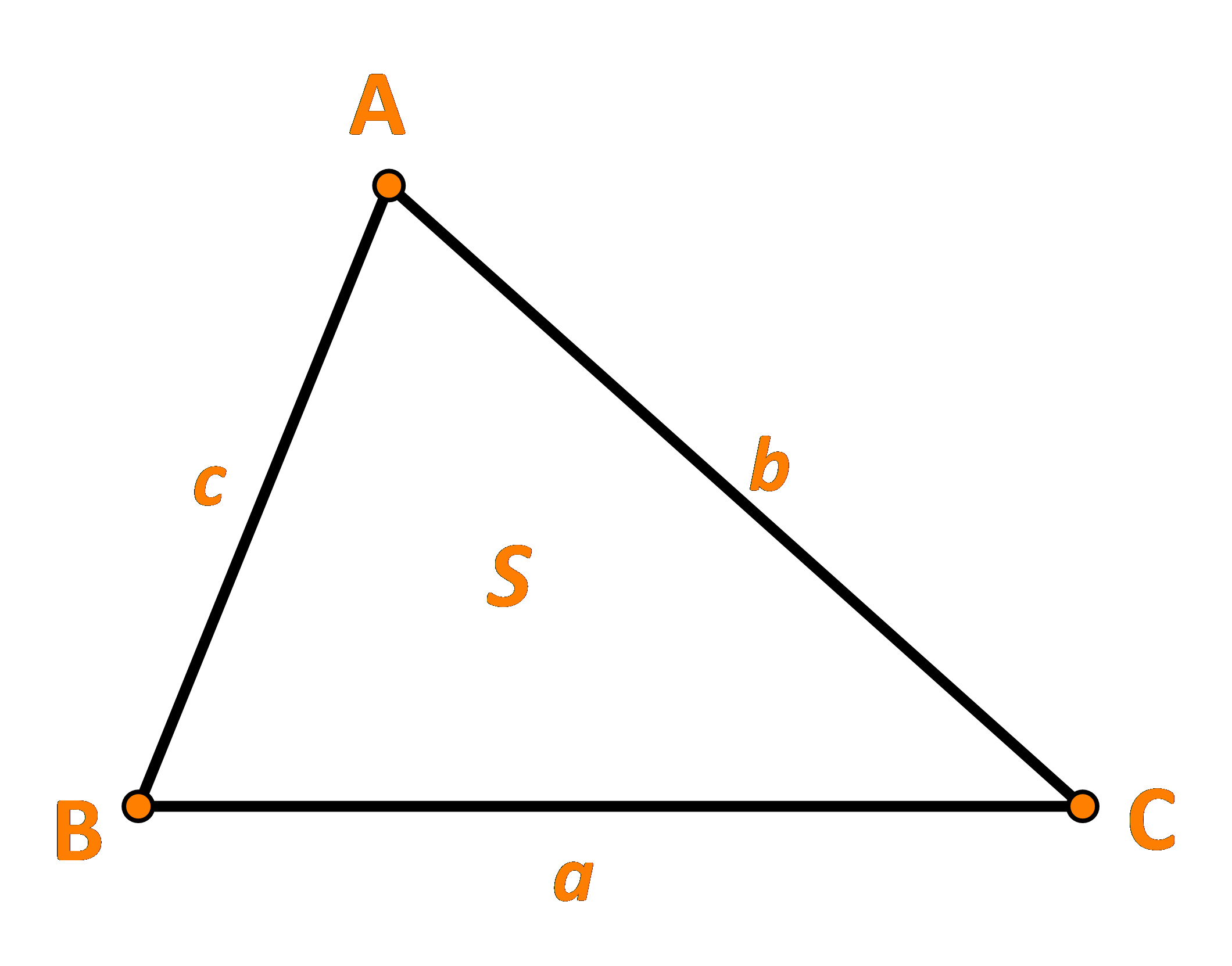
Hoạt động 4 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = c, AC = b, BC = a. Kẻ đường cao BH.
a) Tính BH theo c và sin A.
b) Tính diện tích S của tam giác ABC theo b, c, và sin A.
Lời giải:
a) Xét các trường hợp:
+ Với
Xét tam giác vuông AHB, ta có: BH = AB . sin A = c sin A.
+ Với
Khi đó, BH = BA = c = c sin A.
+ Với
Xét tam giác AHB vuông, ta có: .
Do đó BH = AB . sin(180° – ) = AB . sin A = c sin A.
Như vậy, trong mọi trường hợp ta đều có BH = c sin A.
b) Ta có:
Phương pháp giải:
Bước 1: Tính AC, bằng cách áp dụng định lí sin trong tam giác ABC.
Bước 2: Tính . Suy ra diện tích tam giác ABC bằng công thức
Lời giải:
Áp dụng định lí sin trong tam giác ABC, ta có:
Lại có:
Diện tích tam giác ABC là:
Vậy diện tích tam giác ABC là 85,2.
a) Từ định lí cosin, chứng tỏ rằng:
ở đó
b) Bằng cách sử dụng công thức ,hãy chứng tỏ rằng:
Phương pháp giải:
Bước 1: Tính cos A theo a, b, c.
Bước 2: Tính sin A theo cos A.
Lời giải:
Áp dụng định lí cosin trong tam giác ABC ta có:
Mà .
Đặt
Ta có:
b) Ta có:
Mà
III. Áp dụng vào bài toán thực tiễn
Lời giải:
Gọi A là vị trí đứng của Nam, B là điểm cao nhất của cây, C là vị trí gốc cây.
Gọi H là hình chiếu của A trên BC. Ta có hình vẽ:
TH1: Cây cao hơn tòa nhà
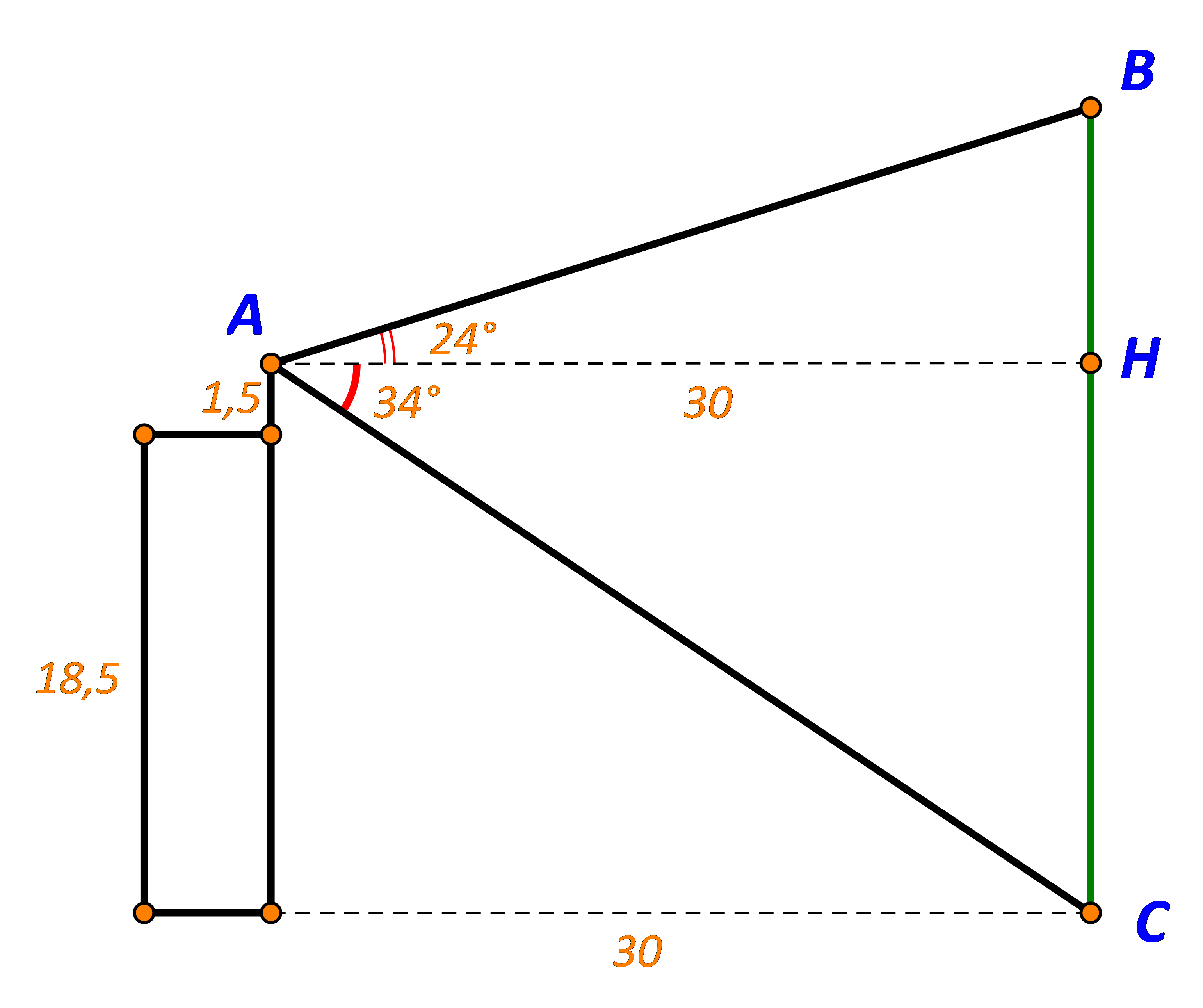
TH2: Cây thấp hơn tòa nhà
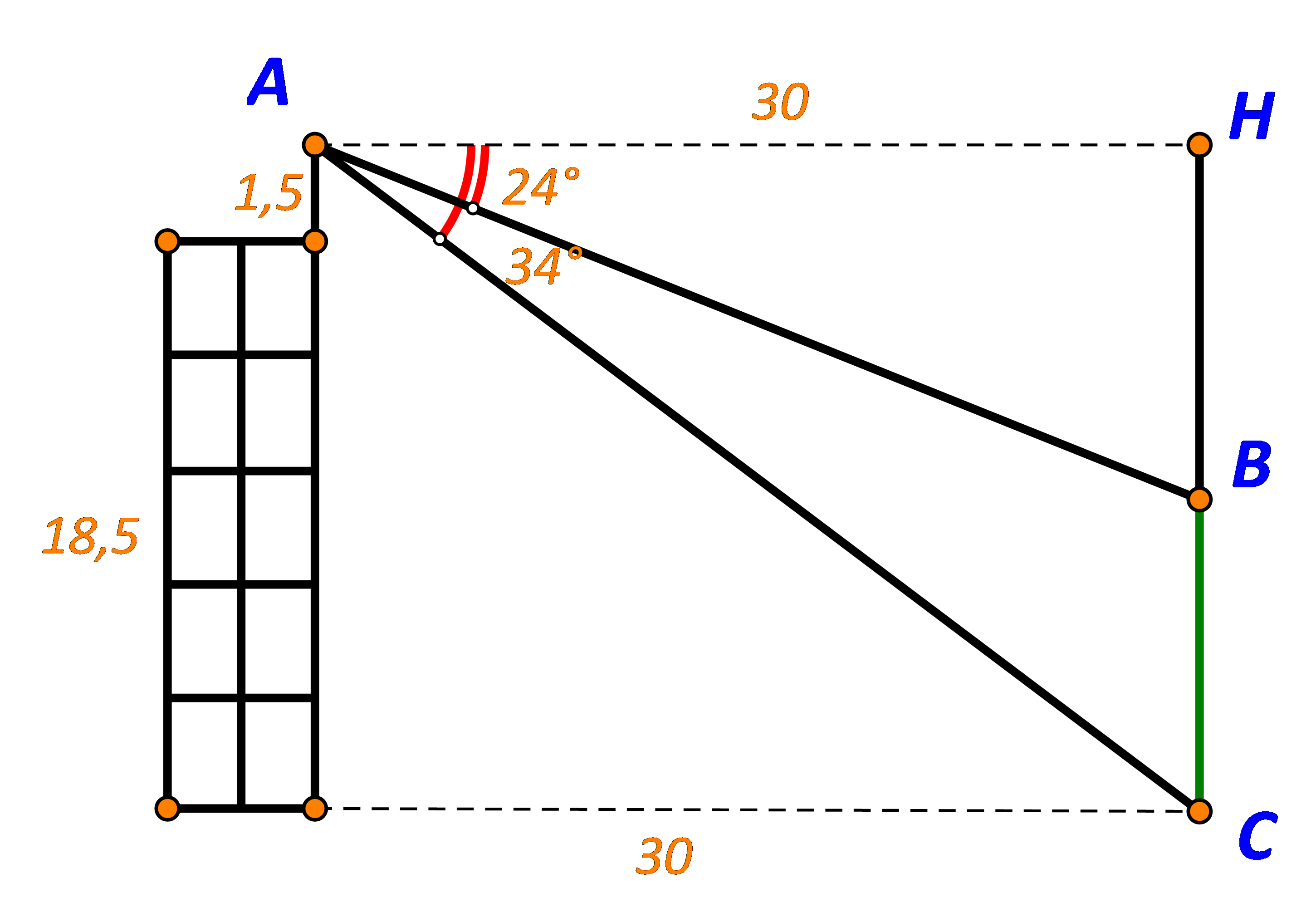
Bài tập
Bài 1 trang 77 Toán 10 Tập 1: Cho tam giác ABC có Tính:
a) Độ dài cạnh AB.
b) Số đo các góc A, B.
c) Diện tích tam giác ABC.
Phương pháp giải:
a) Áp dụng định lí cosin trong tam giác ABC (tại đỉnh C).
b)
Bước 1: Tính sin A, bằng cách áp dụng định lí sin trong tam giác ABC: .
Bước 2: Tính góc A, từ đó suy ra góc B.
c) Tính diện tích tam giác ABC bằng công thức
Lời giải:
a) Áp dụng định lí cosin trong tam giác ABC ta có:
b) Áp dụng định lí sin trong tam giác ABC, ta có:
hoặc (Loại)
Khi đó:
c)
Diện tích tam giác ABC là:
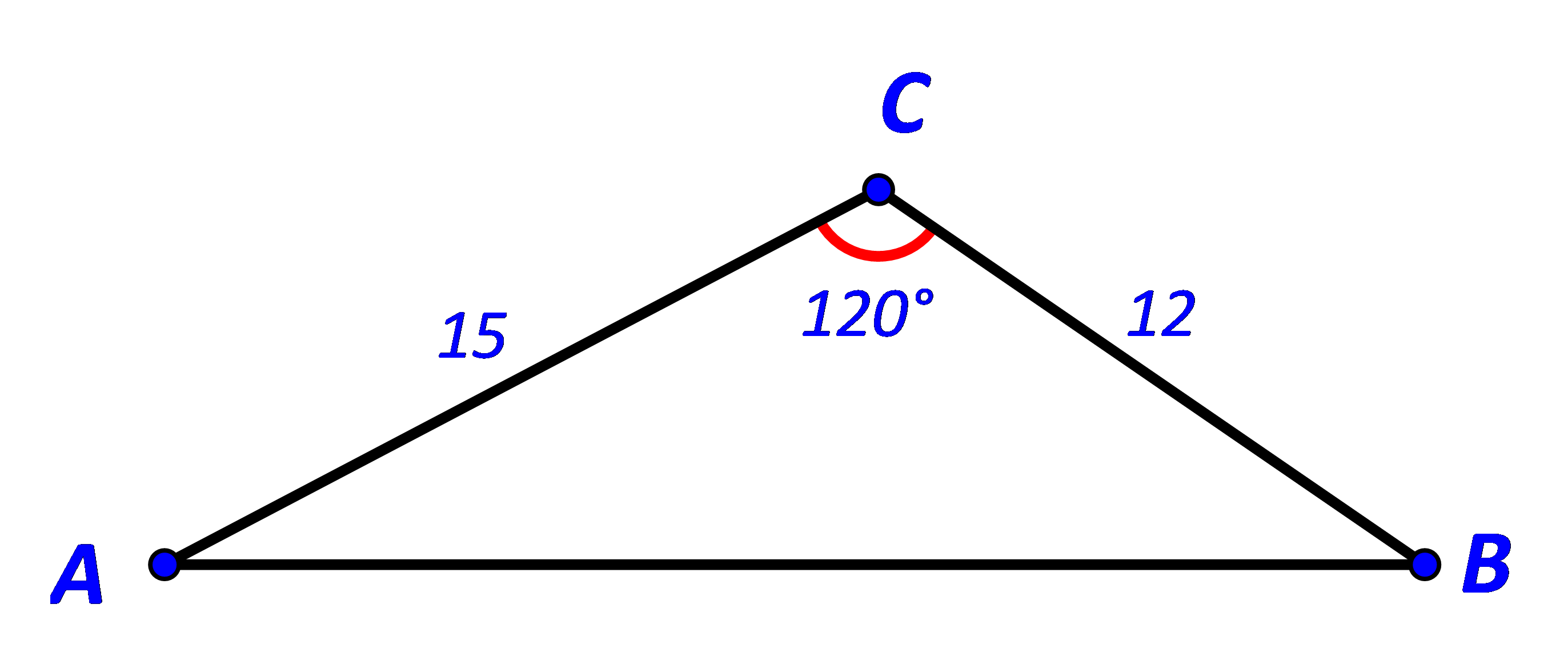
Bài 2 trang 77 Toán 10 Tập 1: Cho tam giác ABC có Tính độ dài cạnh AC.
Phương pháp giải:
Bước 1: Tính sin C, bằng cách áp dụng định lí sin trong tam giác ABC:
Bước 2: Suy ra góc . Tính AC bằng cách áp dụng định lí cosin:
Lời giải:
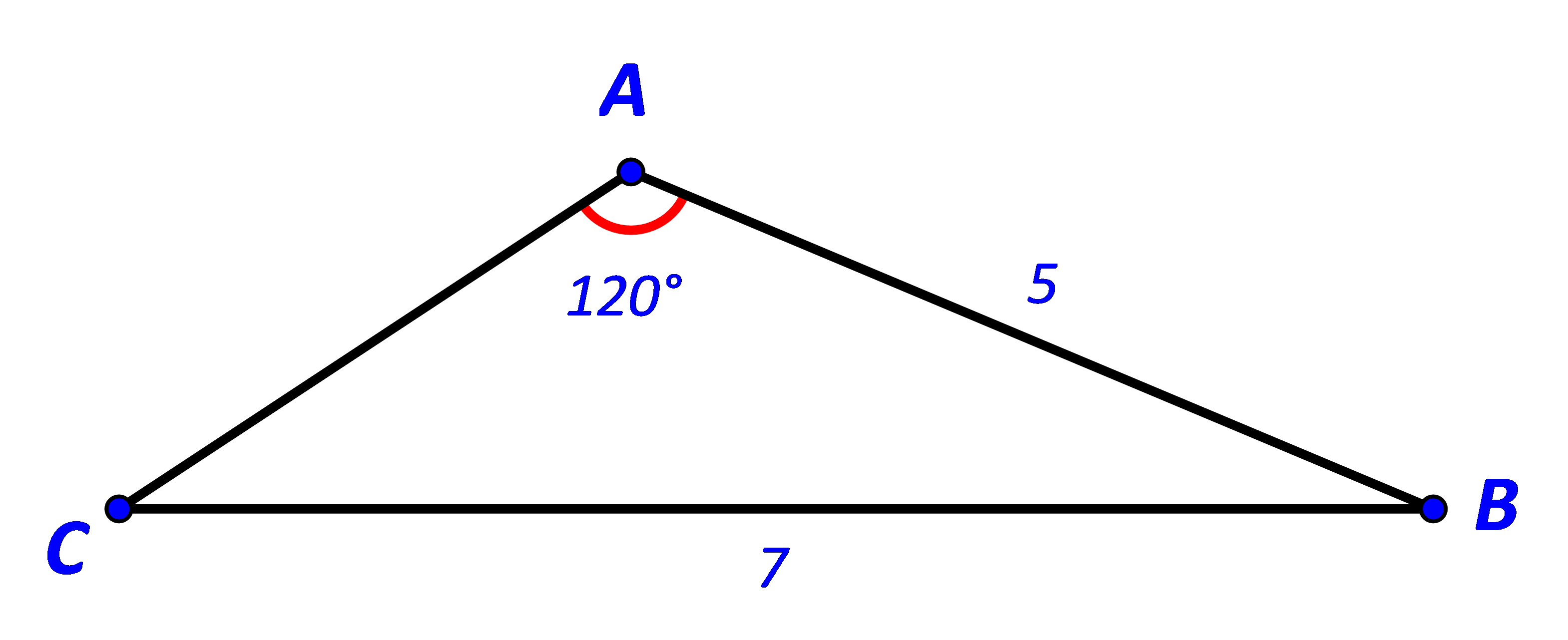
Áp dụng định lí sin trong tam giác ABC ta có:
hoặc (Loại)
Ta có:
Áp dụng định lí cosin trong tam giác ABC ta có:
Vậy độ dài cạnh AC là 3.
Bài 3 trang 77 Toán 10 Tập 1: Cho tam giác ABC có Tính:
a) Độ dài các cạnh AC, BC
b) Diện tích tam giác ABC.
Phương pháp giải:
a)
Bước 1: Tính .
Bước 2: Tính AC, BC bằng cách áp dụng định lí sin trong tam giác ABC:
b)
Tính diện tích tam giác ABC bằng một trong 4 công thức sau:
+)
+)
Lời giải:
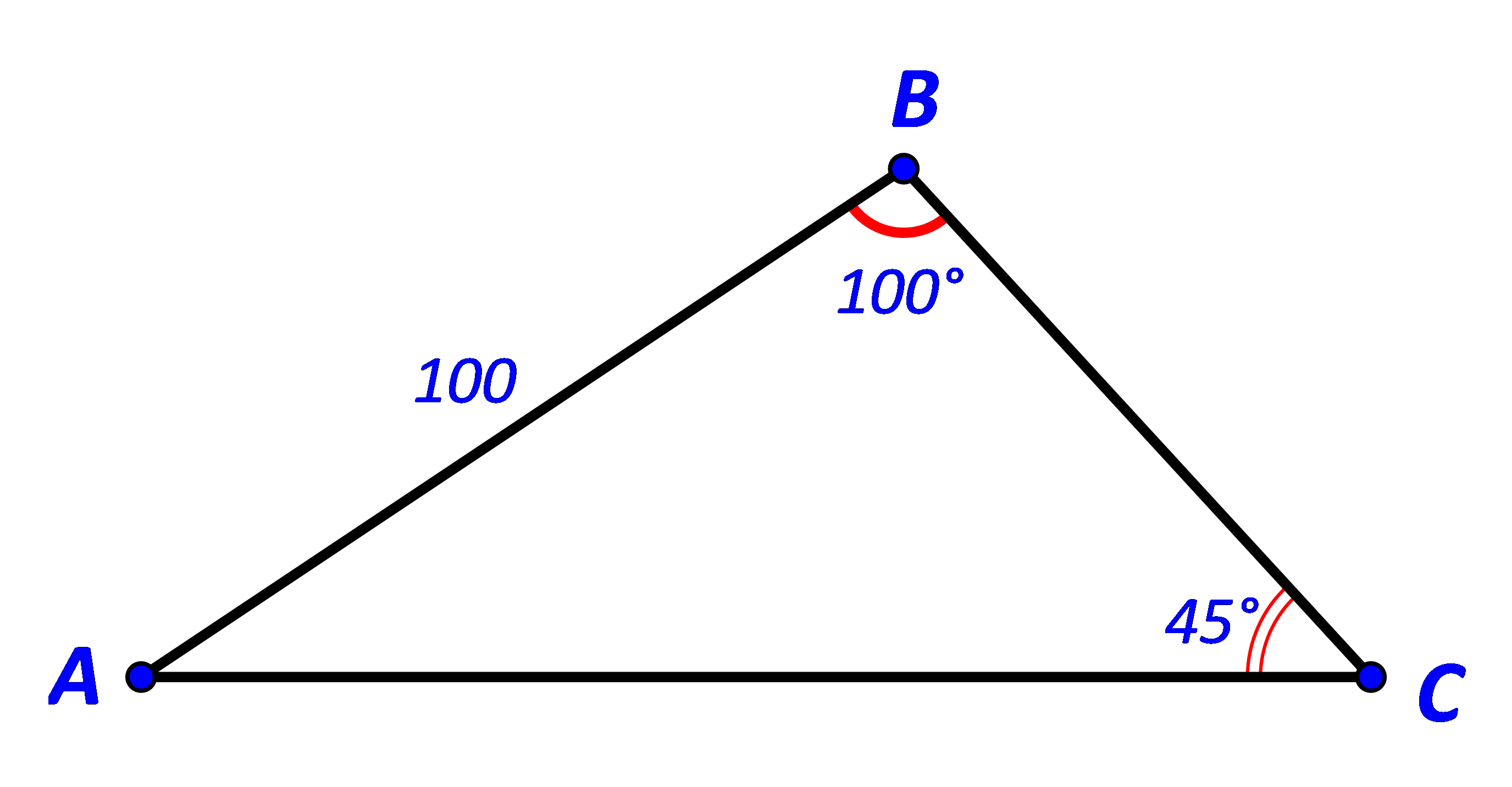
a)
Ta có:
Áp dụng định lí sin trong tam giác ABC ta có:
b) Diện tích tam giác ABC là:
Bài 4 trang 77 Toán 10 Tập 1: Cho tam giác ABC có Tính:
a) Số đo các góc A, B, C.
b) Diện tích tam giác ABC.
Phương pháp giải:
a)
Bước 1: Áp dụng định lí cosin trong tam giác ABC, suy công thức tính theo a, b, c.
Bước 2: Tìm góc A, B. Từ đó suy ra góc C.
b) Tính diện tích tam giác ABC bằng một trong 4 công thức sau:
+)
+)
Lời giải:
a) Áp dụng định lí cosin trong tam giác ABC, ta có:
Thay
b)
Diện tích tam giác ABC là:
Bài 5 trang 77 Toán 10 Tập 1: Tính độ dài cạnh AB trong mỗi trường hợp sau:
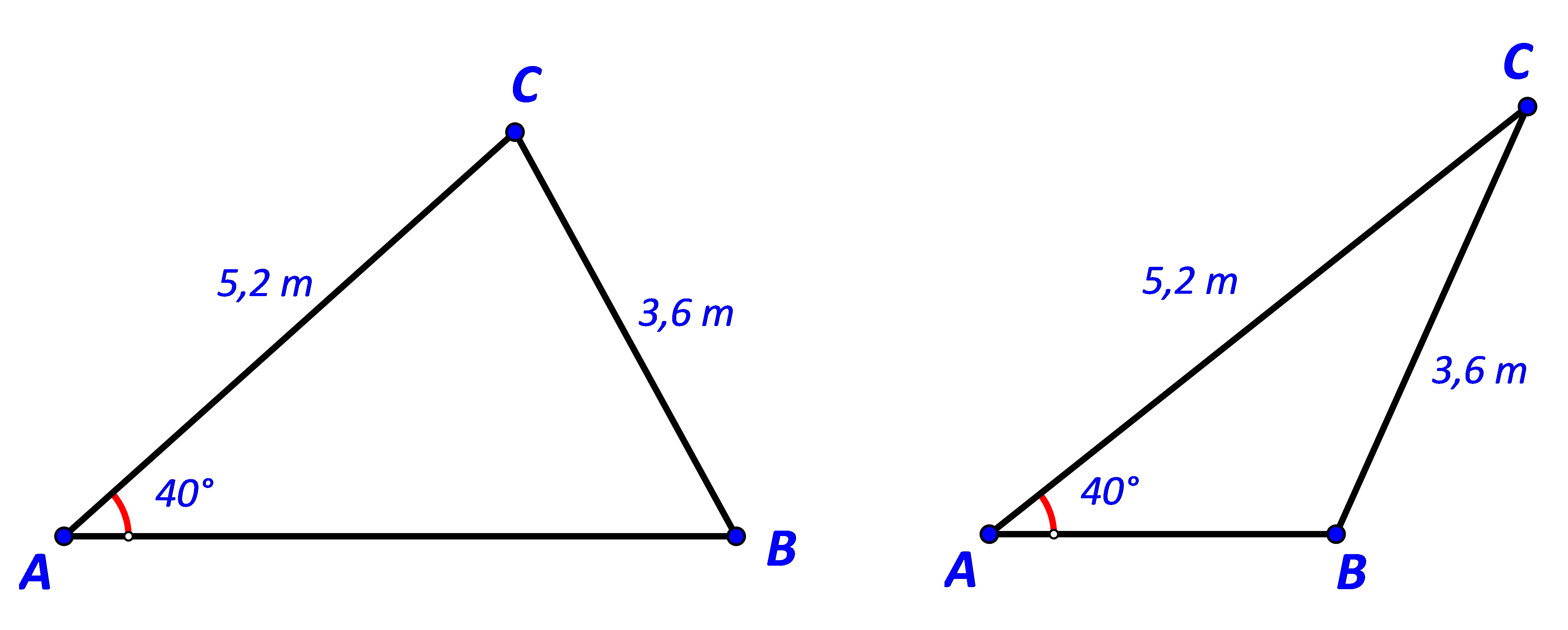
Phương pháp giải:
Bước 1: Tính góc B: Áp dụng định lí sin trong tam giác ABC.
Bước 2: Tính góc C. Áp dụng định lí sin hoặc định lí cosin để tìm AB
Lời giải:
Áp dụng định lí sin trong tam giác ABC, ta có:
hoặc
Trường hợp 1:
Ta có:
Áp dụng định lí sin trong tam giác ABC, ta có:
Trường hợp 2:
Ta có:
Áp dụng định lí sin trong tam giác ABC, ta có:
Vậy AB = 5,32 hoặc AB = 2,65.
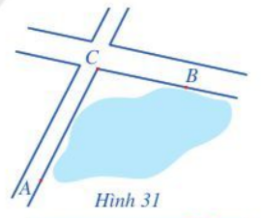
Phương pháp giải:
Bước 1: Đổi độ dài AC, CB về cùng đơn vị mét.
Bước 2: Tính AB: Áp dụng định lí cosin trong tam giác BAC:
Lời giải:
Đổi: 1 km = 1000 m. Do đó AC = 1000 m.
Áp dụng định lí cosin trong tam giác ABC ta có:
Vậy khoảng cách AB là 1433,2 m.
Phương pháp giải:
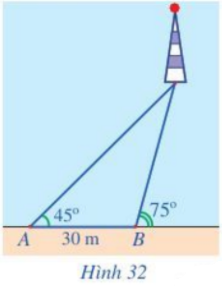
Gọi C là vị trí ngọn hải đăng, H là hình chiếu của C trên AB.
Bước 1: Tính góc ACB, ABC.
Bước 2: Tính AC bằng cách áp dụng định lí sin trong tam giác ABC:
Bước 3: Tính AH bằng công thức: AH = AC. cos A.
Lời giải:
Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.
Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
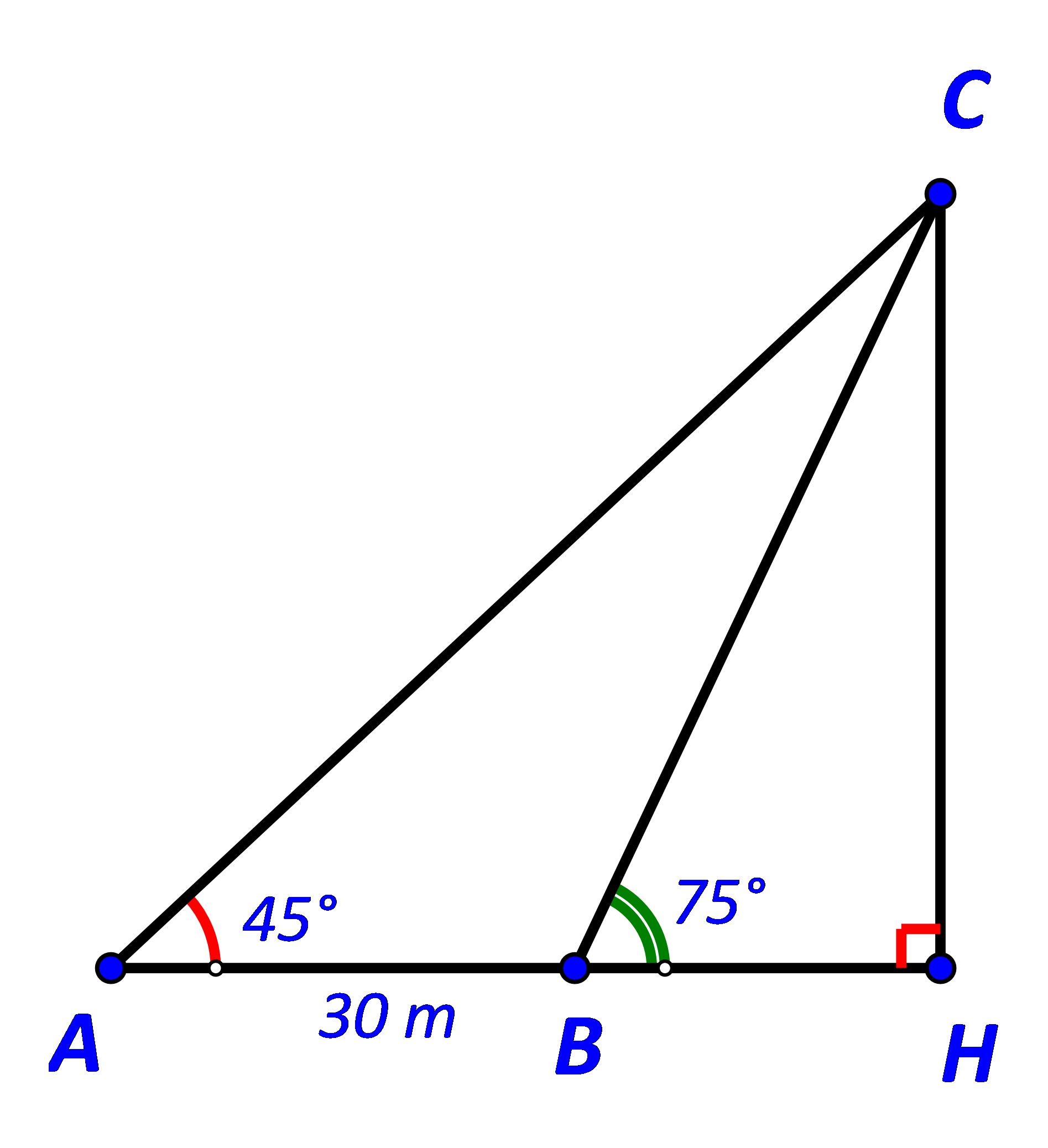
Ta có:
Áp dụng định lí sin trong tam giác ABC ta có:
Tam giác ACH vuông tại H nên ta có:
Vậy ngọn hải đăng cách bờ biển 56 m.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.