Toptailieu.vn giới thiệu Giải SGK Toán 10 Bài 5 (Kết nối tri thức): Giá trị lượng giác của một góc từ 0° đến 180° chi tiết sách Toán 10 Tập 1 Kết nối tri thức với cuộc sống giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:
Toán 10 Kết nối tri thức Bài 5: Giá trị lượng giác của một góc từ 0° đến 180°
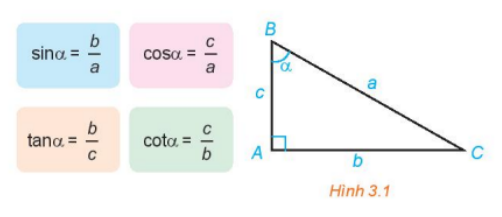
Lời giải:
Góc cho trước,.
Trên nửa đường tròn đơn vị, vẽ điểm sao cho
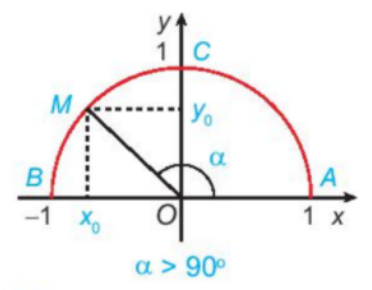
Khi đó:
1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC
b) Khi , nêu mối quan hệ giữa với hoành độ và tung độ của điểm M.
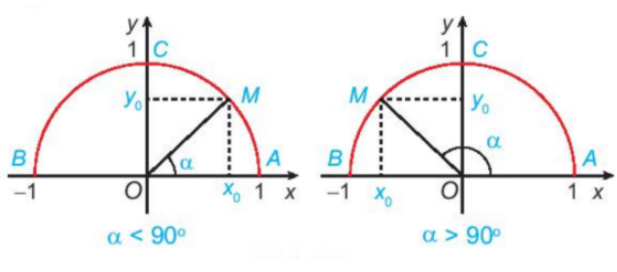
Phương pháp giải:
a) Quan sát góc trong các trường hợp tương ứng. Khi ấy M thuộc cung nào?
b) Khi thì trong đó .
Lời giải:
a) Khi , điểm M trùng với điểm C. (Vì )
Khi , điểm M thuộc vào cung AC (bên phải trục tung)
Khi , điểm M thuộc vào cung BC (bên trái trục tung)
b) Khi , ta có:
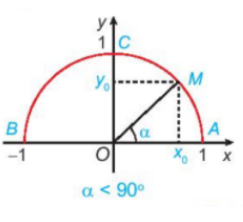
Vì ; tia nên ; tia nên
Vậy là hoành độ của điểm M, là tung độ của điểm M.
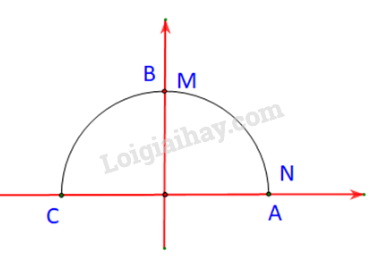
Luyện tập 1 trang 35 Toán lớp 10: Tìm các giá trị lượng giác của góc (H.3.4)
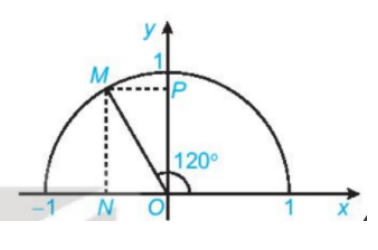
Phương pháp giải:
Gọi M là điểm trên nửa đường tròn đơn vị sao cho
Khi đó hoành độ và tung độ của điểm M lần lượt là các giá trị
Từ đó suy ra
Lời giải:
Gọi M là điểm trên nửa đường tròn đơn vị sao cho
Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
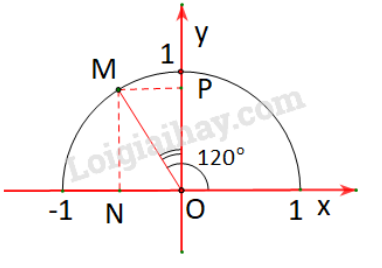
Vì nên M nằm bên trái trục tung.
Khi đó:
Vì nên và
Vậy các tam giác và vuông tại N, p và có một góc bằng
(Trong tam giác vuông, cạnh đối diện góc bằng một nửa cạnh huyền)
Và
Vậy điểm M có tọa độ là .
Và
Chú ý: Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc
Với các loại máy tính fx-570 ES (VN hoặc VN PLUS) ta làm như sau:
Bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ)
Tính , bấm phím: sin 1 2 0 ’’’ = ta được kết quả là
Tính ,bấm phím: cos 1 2 0 ’’’ = ta được kết quả là
Tính , bấm phím: tan 1 2 0 ’’’ = ta được kết quả là
( Để tính , ta tính )
2. MỐI QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU
Hoạt động 2 trang 36 Toán lớp 10: Nêu nhận xét về vị trí của hai điểm M, M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa và , giữa và .
Phương pháp giải:
Nhận xét vị trí của M và M’ trong mỗi trường hợp:
Khi : tương ứng là hoành độ và tung độ của điểm M.
Lời giải:
M, M’ là hai điểm trên nửa đường tròn đơn vị tương ứng với hai góc và .
Giả sử . Khi đó
Trường hợp 1:
Khi đó
Tức là M và M’ lần lượt trùng nhau và trùng với B.
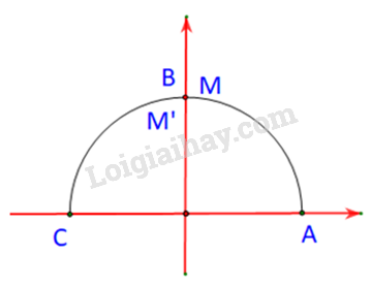
Và
Không tồn tại với
Trường hợp 2:
M nằm bên phải trục tung
M’ nằm bên trái trục tung
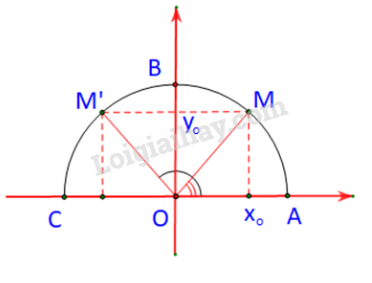
Dễ thấy:
Xét tam giác và tam giác ta có:
OB chung
Hay OB là trung trực của đoạn thẳng MM’.
Nói cách khác M và M’ đối xứng với nhau qua trục tung.
Mà nên
Trường hợp 3:
Khi đó M nằm bên trái trục tung và M’ nằm bên phải trục tung.
Tương tự ta cũng chứng minh được M và M’ đối xứng với nhau qua trục tung.
Như vậy
Kết luận: Với mọi , ta luôn có
Luyện tập 2 trang 36 Toán lớp 10: Trong Hình 3.6, hai điểm M, N ứng với hai góc phụ nhau và (). Chứng mình rằng . Từ đó nêu mối quan hệ giữa và .
Phương pháp giải:
Nhận xét vị trí của M và N trong mỗi trường hợp:
Khi : tương ứng là hoành độ và tung độ của điểm M.
Lời giải:
Trường hợp 1:
Khi đó
Tức là M và N lần lượt trùng nhau với B và A.
Và
Trường hợp 2:
M và N cùng nằm bên trái phải trục tung.
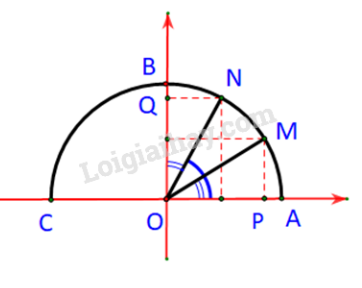
Ta có:
Dễ thấy:
Xét hai tam giác vuông và tam giác ta có:
Mà nên . Nói cách khác:
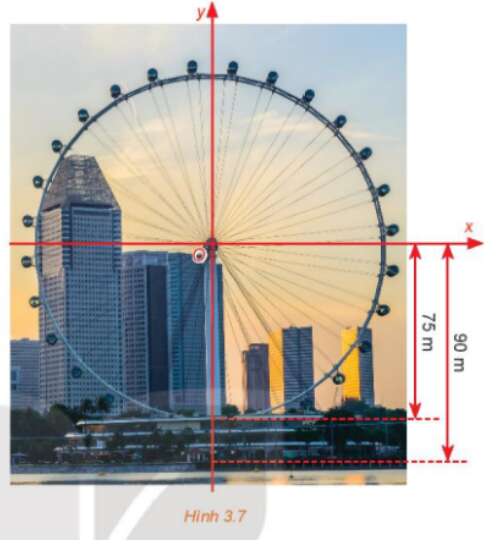
Câu hỏi vận dụng trang 37 Toán lớp 10: Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét?
Phương pháp giải:
Bước 1: Giả sử chiều quay của chiếc đu quay. Xác định vị trí của cabin sau 20 phút.
Bước 2: Dựa vào giá trị lượng giác của góc, xác định khoảng cách từ cabin đến Ox (trong hình H.3.7)
Bước 3: Suy ra độ cao của người đó sau 20 phút quay.
Lời giải:
Giả sử chiếc đu quay quay theo chiều kim đồng hồ.
Gọi M là vị trí của cabin, M’ là vị trí của cabin sau 20 phút và các điểm A A’, B, H như hình dưới.
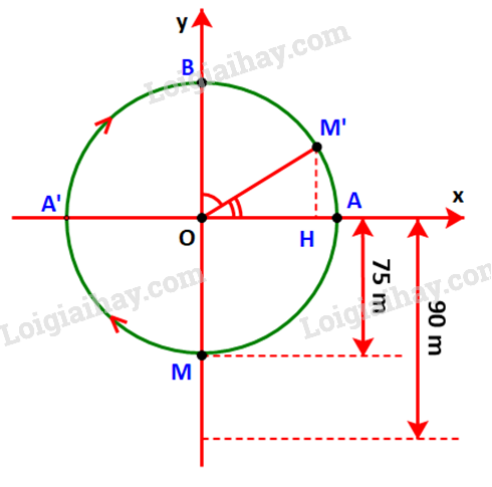
Vì đi cả vòng quay mất 30 phút nên sau 20 phút, cabin sẽ đi quãng đường bằng chu vi đường tròn.
Sau 15 phút cabin đi chuyển từ điểm M đến điểm B, đi được chu vi đường tròn.
Trong 5 phút tiếp theo cabin đi chuyển từ điểm B đến điểm M’ tương ứng chu vi đường tròn hay cung .
Do đó:
Độ cao của người đó là: 37,5 + 90 = 127,5 (m).
Vậy sau 20 phút quay người đó ở độ cao 127,5 m.
BÀI TẬP
a)
b)
c)
Lời giải a
a)
Phương pháp giải:
Bước 1: Đưa GTLG của các góc về GTLG của các góc
Bước 2: Sử dụng bảng giá trị lượng giác của một số góc đặc biệt.
Lời giải:
Đặt
Ta có:
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
Lời giải b
b)
Phương pháp giải:
Bước 1: Đưa GTLG của các góc về GTLG của các góc
Bước 2: Sử dụng bảng giá trị lượng giác của một số góc đặc biệt.
Lời giải:
Đặt
Ta có:
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
Lời giải c
c)
Phương pháp giải:
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt.
Lời giải:
Đặt
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
Bài 3.2 trang 37 Toán lớp 10: Đơn giản các biểu thức sau:
Lời giải a
a)
Phương pháp giải:

Lời giải:
Ta có:
Lời giải b
b) với .
Phương pháp giải:

Lời giải:
Ta có:
Bài 3.3 trang 37 Toán lớp 10: Chứng minh các hệ thức sau:
a) .
b)
c)
Lời giải a
a) .
Phương pháp giải:
Bước 1: Vẽ đường tròn lượng giác, lấy điểm M biểu diễn góc bất kì.
Bước 2: Xác định ( tương ứng với tung độ và hoành độ của điểm M).
Bước 3: Suy ra đẳng thức cần chứng minh.
Lời giải:
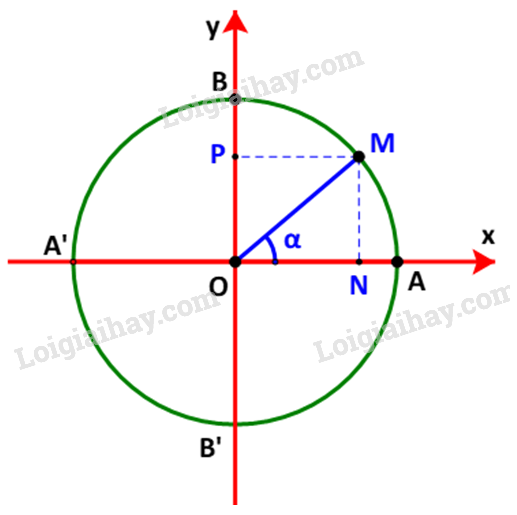
Gọi M(x;y) là điểm trên đường tròn đơn vị sao cho . Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Ta có: (1)
Mà (2)
Từ (1) và (2) suy ra (do vuông tại N)
(vì OM =1). (đpcm)
Lời giải b
b)
Phương pháp giải:
Bước 1: Viết dưới dạng , thay vào vế trái.
Bước 2: Biến đổi vế trái bằng cách quy đồng, kết hợp với ý a) để suy ra vế phải.
Lời giải:
Ta có:
Mà theo ý a) ta có với mọi góc
(đpcm)
Lời giải c
c)
Phương pháp giải:
Bước 1: Viết dưới dạng , thay vào vế trái.
Bước 2: Biến đổi vế trái bằng cách quy đồng, kết hợp với ý a) để suy ra vế phải.
Lời giải:
Ta có:
Mà theo ý a) ta có với mọi góc
(đpcm)
Bài 3.4 trang 37 Toán lớp 10: Cho góc thỏa mãn
Tính giá trị biểu thức:
Phương pháp giải:
Chia cả tử và mẫu của P cho .
Lời giải:
Vì nên
Cách 2:
Ta có:
Vì nên .
Mà
Lại có:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.