Với giải Vận dụng 1 trang 82 Toán 11 Tập 1 Chân trời sáng tạo chi tiết trong Bài 3: Hàm số liên tục giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Vận dụng 1 trang 82 Toán 11 Tập 1 | Chân trời sáng tạo Giải Toán lớp 11
Vận dụng 1 trang 82 Toán 11 Tập 1: Tại một xưởng sản xuất bột đá thạch anh, giá bán (tính theo nghìn đồng) của x (kg) bột đá thạch anh được tính theo công thức sau:
(k là một hằng số).
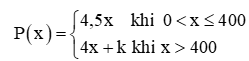
a) Với k = 0, xét tính liên tục của hàm số P(x) trên (0; +∞).
b) Với giá trị nào của k thì hàm số P(x) liên tục trên (0; +∞)?
Lời giải:
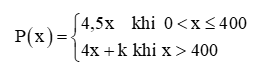
a) Với k = 0, hàm số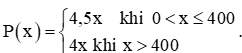 
+) Lấy x0 ∈ (0; 400) khi đó P(x) = 4,5x
Suy ra
Do đó P(x) liên tục trên (0; 400).
+) Tại x0 = 400, ta có:
.
.
Suy ra . Do đó không tồn tại .
Vì vậy hàm số không liên tục tại x = 400.
+) Lấy x0 ∈ (400; +∞) khi đó P(x) = 4x
Suy ra
Do đó P(x) liên tục trên (400; +∞) .
Vậy hàm số liên tục trên (0; 400) và (400; +∞).
b) Để hàm số P(x) liên tục trên (0; +∞) thì P(x) phải liên tục trên x0 = 400.
Do đó .
Vậy với k = 200 thì hàm số liên tục trên (0; +∞).
Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Hoạt động khám phá 1 trang 80 Toán 11 Tập 1: Cho hàm số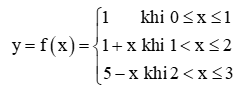 
có đồ thị như Hình 1.
Thực hành 1 trang 81 Toán 11 Tập 1: Xét tính liên tục của hàm số:
Hoạt động khám phá 2 trang 81 Toán 11 Tập 1: Cho hàm số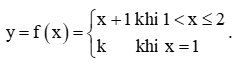 
.
Thực hành 2 trang 82 Toán 11 Tập 1: Xét tính liên tục của hàm số: trên [1; 2].
Hoạt động khám phá 3 trang 82 Toán 11 Tập 1: Tìm tập xác định của mỗi hàm số đã cho.
Thực hành 3 trang 83 Toán 11 Tập 1: Xét tính liên tục của hàm số
Thực hành 4 trang 83 Toán 11 Tập 1: Cho hàm số f(x) =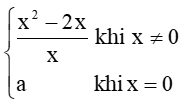 
. Tìm a để hàm số y = f(x) liên tục trên ℝ.
Thực hành 5 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số:
Bài 1 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số sau:
Bài 2 trang 84 Toán 11 Tập 1: Cho hàm số f(x) =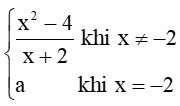 
. Tìm a để hàm số f(x) liên tục trên ℝ.
Bài 3 trang 85 Toán 11 Tập 1: Xét tính liên tục của hàm số sau:
Bài 4 trang 85 Toán 11 Tập 1: Cho hàm số f(x) = 2x – sinx, g(x). Xét tính liên tục của hàm số y
Xem thêm lời giải sách giáo khoa Toán 11 Chân trời sáng tạo hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn. Hàm số F(r) có liên tục trên (0; +∞) không?
