Toptailieu.vn biên soạn và giới thiệu giải Giải Vở thực hành Toán 8 (Kết nối tri thức) Bài 1: Đơn thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập Toán 8. Mời các bạn cùng đón xem:

Giải Vở thực hành Toán 8 (Kết nối tri thức) Bài 1: Đơn thức

Câu 1 trang 5 VTH Toán 8 Tập 1: Cho các biểu thức A = 2(x + 1)y²; B = −0,7xyx²z³;  và  Hai đơn thức trong số các biểu thức đã cho là:

A. A và B.

B. B và C.

C. B và D.

D. C và D.

Lời giải:

Đáp án đúng là: B

Các biểu thức là đơn thức gồm −0,7xyx²z³ và 

Vậy B và C là hai đơn thức trong 4 biểu thức trên.

Câu 2 trang 5 VTH Toán 8 Tập 1: Cho các đơn thức A = (0,3 + π)x²y;  C = −xyxz² và  Hai đơn thức thu gọn trong các đơn thức đã cho là:

A. A và B.

B. A và C.

C. A và D.

D. B và C.

Lời giải:

Đáp án đúng là: C

Các đơn thức thu gọn bao gồm (0,3 + π)x²y và 

Vậy A và D là hai đơn thức thu gọn trong các đơn thức trên.

Câu 3 trang 6 VTH Toán 8 Tập 1: Sau khi thu gọn các đơn thức A = 2xyzx; B = −3yxzy; C = 4zxyz và D = −5x²yzy, đơn thức đồng dạng với đơn thức −6x²yz là:

A. A.

B. B.

C. C.

D. D.

Lời giải:

Đáp án đúng là: A

Ta có đơn thức thu gọn của các đơn thức trên là:

A = 2xyzx = 2x²yz; B = −3yxzy = −3xy²z; C = 4zxyz = 4xyz² và D = −5x²yzy = −5x²y²z.

Đơn thức đồng dạng với đơn thức −6x²yz là đơn thức có phần biến x²yz.

Vậy đơn thức đó là 2x²yz.

Câu 4 trang 6 VTH Toán 8 Tập 1: Chọn phương án đúng.

Cho hai đơn thức M = 5,5x³y²z và N = −1,5x³y²z. Tổng và hiệu của chúng là:

A. M + N = 4x³y²z; M – N = 6x³y²z.

B. M + N = 4x²y³z; M – N = 7x³y²z.

C. M + N = 4x³y²z; M – N = 7x³y²z.

D. M + N = 4x³y²z; M – N = 7x²y³z.

Lời giải:

Đáp án đúng là: C

Ta có:

• M + N = 5,5x³y²z + (−1,5x³y²z)

= x³y²z(5,5 − 1,5) = 4x³y²z;

• M – N = 5,5x³y²z − (−1,5x³y²z)

= (5,5 + 1,5)x³y²z = 7x³y²z.

Vậy đáp án đúng là C.

C – BÀI TẬP

Bài 1 trang 6 VTH Toán 8 Tập 1: Trong các biểu thức sau, biểu thức nào là đơn thức?

−x; (1 + x)y²;  0;  

Lời giải:

Các đơn thức là: 

Biểu thức (1 + x)y²  không phải là đơn thức vì đơn thức có dạng tích của những số và biến.

Bài 2 trang 6 VTH Toán 8 Tập 1: Cho các đơn thức:

A = 4x(−2)x²y; B = 12,75xyz;  

a) Liệt kê các đơn thức thu gọn trong các đơn thức đã cho và thu gọn các đơn thức còn lại.

b) Với mỗi đơn thức nhận được, hãy cho biết hệ số, phần biến và bậc của nó.

Lời giải:

a) Các đơn thức thu gọn là B và D. Ta thu gọn hai đơn thức còn lại:

A = 4x(−2)x²y = −8x³y; 

b) Hệ số, phần biến và bậc của từng đơn thức được ghi lại trong bảng sau:

Bài 3 trang 6 VTH Toán 8 Tập 1: Thu gọn rồi tính giá trị của mỗi đơn thức sau:

a)  khi x = −2;                    

b) B = xyz(−0,5)y²z khi x = 4; y = 0,5; z = 2.

Lời giải:

a)  Tại x = −2 và  ta có:

b) B = xyz(−0,5)y²z = −0,5xy³z². Tại x = 4; y = 0,5 và z = 2, ta có:

B = −0,5 . 4 . (0,5)³ . 2² = −0,5 . 4 . 0,125 . 4 = −1.

Bài 4 trang 7 VTH Toán 8 Tập 1: Sắp xếp các đơn thức sau thành từng nhóm, mỗi nhóm chứa tất cả các đơn thức đồng dạng với nhau: 3x³y²; −0,2x²y³; 7x³y²; −4y;  

Lời giải:

Nhóm thứ nhất gồm các đơn thức 3x³y² và 7x³y².

Nhóm thứ hai gồm các đơn thức −0,2x²y³ và 

Nhóm thứ ba gồm các đơn thức −4y và 

Bài 5 trang 7 VTH Toán 8 Tập 1: Tính tổng của các đơn thức trong mỗi nhóm ở bài tập 4.

Lời giải:

Với nhóm thứ nhất ta có: 3x³y² + 7x³y² = (3 + 7)x³y² = 10x³y².

Với nhóm thứ hai ta có: 

hoặc 

Với nhóm thứ ba ta có: 

Bài 6 trang 7 VTH Toán 8 Tập 1: Rút gọn rồi tính giá trị của biểu thức

 khi x = −2 và y = 1.

Lời giải:

• Rút gọn: 

• Tại x = −2 và y = 1 ta có: S = (−2) . (−2)². 1⁵= (−2) . 4 . 1 = −8.

Bài 7 trang 7 VTH Toán 8 Tập 1: Tính tổng của bốn đơn thức: 2x²y³;  −14x²y³; 

Lời giải:

Ta có: 

Bài 8 trang 7 VTH Toán 8 Tập 1: Một mảnh đất có dạng như phần tô màu xám trong hình bên cùng với kích thước (tính bằng mét) được ghi trên đó. Hãy tìm đơn thức (thu gọn) với hai biến x và y biểu thị diện tích của mảnh đất đã cho bằng hai cách:

Cách 1. Tính tổng diện tích của hai hình chữ nhật ABCD và EFGC.

Cách 2. Lấy diện tích của hình chữ nhật HFGD trừ đi diện tích của hình chữ nhật HEBA.

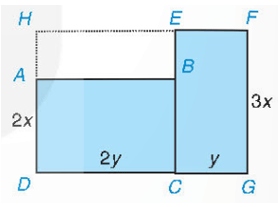
Lời giải:

Cách 1. Ta có S_ABCD = 2x . 2y = 4xy; S_EFGC = 3x . y = 3xy.

Vậy diện tích mảnh đất là S = 4xy + 3xy = 7xy.

Cách 2. Ta có S_HFGD = 3x . (2y + y) = 3x . 3y = 9xy;

S_HEBA = 2y . (3x – 2x) = 2y . x = 2xy.

Vậy diện tích mảnh đất là S = 9xy – 2xy = 7xy.

Xem thêm các bài Giải Vở thực hành Toán 8 (Kết nối tri thức) hay, chi tiết khác:

Bài 2: Đa thức

Bài 3: Phép cộng và phép trừ đa thức

Luyện tập chung trang 13

Bài 4: Phép nhân đa thức

Bài 5: Phép chia đa thức cho đơn thức