Từ đồ thị hàm số y = cos x, hãy vẽ các đồ thị hàm số sau

Với Giải Bài 1.21 trang 18 SBT Toán 11 Tập 1 trong Bài 3: Hàm số lượng giác Sách bài tập Toán lớp 11 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán lớp 11.

Từ đồ thị hàm số y = cos x, hãy vẽ các đồ thị hàm số sau

Bài 1.21 trang 18 SBT Toán 11 Tập 1: Từ đồ thị hàm số y = cos x, hãy vẽ các đồ thị hàm số sau:

a) y = – cos x;

b) y = |cos x|;

c) y = cos x + 1;

d) $y = \cos (x + \frac{π}{2})$ .

Lời giải:

a) Lấy đối xứng đồ thị hàm số y = cos x qua trục hoành ta được đồ thị hàm số y = – cos x.

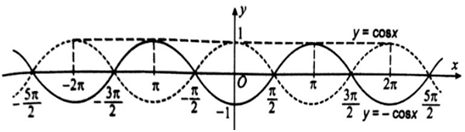
SBT Toán 11 (Kết nối tri thức) Bài 3: Hàm số lượng giác (ảnh 1)

Trong hình trên, đồ thị hàm số y = cos x là đường nét đứt còn đồ thị hàm số y = – cos x là đường nét liền.

b) Ta có Từ đồ thị hàm số y = cos x hãy vẽ các đồ thị hàm số sau

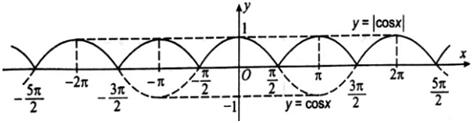
Từ đó, để vẽ đồ thị hàm số y = |cos x| đầu tiên ta vẽ đồ thị hàm số y = cos x, sau đó giữ nguyên phần đồ thị hàm số y = cos x ở phía trên trục Ox và lấy đối xứng qua trục Ox phần đồ thị hàm số y = cos x ở phía dưới trục Ox.

Trong hình dưới đây, đồ thị hàm số y = |cos x| là đường nét liền.

SBT Toán 11 (Kết nối tri thức) Bài 3: Hàm số lượng giác (ảnh 2)

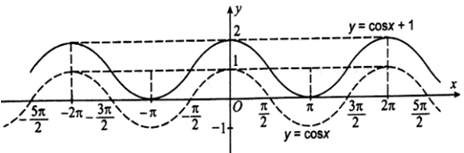
c) Để vẽ đồ thị hàm số y = cos x + 1, đầu tiên ta vẽ đồ thị hàm số y = cos x, sau đó dịch chuyển đồ thị này dọc theo trục Oy lên phía trên 1 đơn vị, ta được đồ thị hàm số y = cosx + 1. Trong hình dưới đây, đồ thị hàm số y = cos x + 1 là đường nét liền.

SBT Toán 11 (Kết nối tri thức) Bài 3: Hàm số lượng giác (ảnh 3)

d) Để vẽ đồ thị hàm số $y = \cos (x + \frac{π}{2})$ đầu tiên ta vẽ đồ thị hàm số y = cos x, sau đó dịch chuyển đồ thị này dọc theo trục Ox sang bên trái $\frac{π}{2}$ đơn vị ta sẽ được đồ thị hàm số $y = \cos (x + \frac{π}{2})$ . Trong hình vẽ dưới đây đồ thị hàm số $y = \cos (x + \frac{π}{2})$ là đường nét liền.

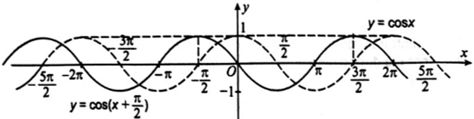
SBT Toán 11 (Kết nối tri thức) Bài 3: Hàm số lượng giác (ảnh 4)

Chú ý rằng $\cos (x + \frac{π}{2}) = - \sin x$ nên đồ thị hàm số $y = \cos (x + \frac{π}{2})$ cũng có thể có được bằng cách lấy đối xứng đồ thị hàm số y = sin x qua trục Ox.