Với Giải trang 18 SBT Toán lớp 11 trong Bài 3: Hàm số lượng giác Sách bài tập Toán lớp 11 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán lớp 11.

 SBT Toán 11 trang 18 Tập 1 (Kết nối tri thức)

Bài 1.18 trang 18 SBT Toán 11 Tập 1: Xét tính chẵn lẻ của các hàm số sau:

a) $y=\frac{\cos 2x}{x^3}$ ;

b) y = x – sin 3x;

c) $y=\sqrt{1+\cos x}$ ;

d) $y=1+\cos x\sin \left(\frac{3\pi }{2}-2x\right)$ .

Lời giải:

a) Tập xác định của hàm số là D = ℝ \ {0}. Nếu kí hiệu f(x) = $\frac{\cos 2x}{x^3}$  thì với mọi x ∈ D, ta có – x ∈ D và f(– x) = $\frac{\cos 2\left(-x\right)}{{\left(-x\right)}^2}=\frac{\cos 2x}{-x^3}=-\frac{\cos 2x}{x^3}=-f\left(x\right)$ .

Vậy hàm số đã cho là hàm số lẻ.

b) Tập xác định của hàm số là D = ℝ. Nếu kí hiệu f(x) = x – sin 3x thì với mọi x ∈ D, ta có – x ∈ D và f(– x) = (– x) – sin 3(– x) = – x + sin 3x = – (x – sin 3x) = – f(x).

Vậy hàm số đã cho là hàm số lẻ. 

c) Tập xác định của hàm số là D = ℝ. Nếu kí hiệu f(x) = $\sqrt{1+\cos x}$  thì với mọi x ∈ D, ta có – x ∈ D và f(– x) = $\sqrt{1+\cos \left(-x\right)}=\sqrt{1+\cos x}=f\left(x\right)$ .

Vậy hàm số đã cho là hàm số chẵn.

d) Tập xác định của hàm số là D = ℝ.

Ta có $y=1+\cos x\sin \left(\frac{3\pi }{2}-2x\right)$

$=1+\cos x\left(\sin \frac{3\pi }{2}\cos 2x-\cos \frac{3\pi }{2}\sin 2x\right)$

$=1-\cos x\cos 2x$.

Nếu kí hiệu f(x) = 1 – cos x cos 2x  thì với mọi x ∈ D, ta có – x ∈ D và

f(– x) = 1 – cos (– x) cos (– 2x) = 1 – cos x cos 2x = f(x).

Vậy hàm số đã cho là hàm số chẵn.

Bài 1.19 trang 18 SBT Toán 11 Tập 1: Xét tính tuần hoàn của các hàm số sau:

a) y = A sin(ωx + φ) với A > 0;

b) y = A tan(ωx + φ) với A > 0;

c) y = 3 sin 2x + 3cos 2x; 

d) $y=3\sin \left(2x+\frac{\pi }{6}\right)+3\sin \left(2x-\frac{\pi }{3}\right)$ .

Lời giải:

a) Tập xác định của hàm số là D = ℝ.

Nếu kí hiệu f(x) = A sin(ωx + φ) thì với mọi x ∈ D, ta có

 $x+\frac{2\pi }{\omega }\in D,x-\frac{2\pi }{\omega }\in D$và

$f\left(x+\frac{2\pi }{\omega }\right)=A\sin \left(\omega \left(x+\frac{2\pi }{\omega }\right)+\phi \right)$= A sin(ωx + 2π + φ) = A sin(ωx + φ) = f(x).

Vậy hàm số đã cho là hàm số tuần hoàn, chu kì của hàm số này là $\frac{2\pi }{\omega }$ .

b) Nếu kí hiệu D là tập xác định của hàm số f(x) = A tan(ωx + φ) thì với mọi x ∈ D, ta có:

$x+\frac{\pi }{\omega }\in D,x-\frac{\pi }{\omega }\in D$ và

$f\left(x+\frac{\pi }{\omega }\right)=A\tan \left(\omega \left(x+\frac{\pi }{\omega }\right)+\phi \right)$= A tan(ωx + π + φ) = A tan(ωx + φ) = f(x).

Vậy hàm số đã cho là hàm số tuần hoàn, chu kì của hàm số này là $\frac{\pi }{\omega }$ .

c) Ta có 3sin 2x + 3cos 2x = 3(sin 2x + cos 2x) = $3\sqrt{2}\sin \left(2x+\frac{\pi }{4}\right)$ .

Theo câu a, ta suy ra hàm số y = 3sin 2x + 3cos 2x là hàm số tuần hoàn chu kì $\frac{2\pi }{2}=\pi$ .

d) Ta có $y=3\sin \left(2x+\frac{\pi }{6}\right)+3\sin \left(2x-\frac{\pi }{3}\right)$

$=3.2\sin \frac{\left(2x+\frac{\pi }{6}\right)+\left(2x-\frac{\pi }{3}\right)}{2}\cos \frac{\left(2x+\frac{\pi }{6}\right)-\left(2x-\frac{\pi }{3}\right)}{2}$

$=3\sqrt{2}\sin \left(2x-\frac{\pi }{12}\right)$.

Vậy theo câu a, hàm số $y=3\sin \left(2x+\frac{\pi }{6}\right)+3\sin \left(2x-\frac{\pi }{3}\right)$  là hàm số tuần hoàn chu kì $\frac{2\pi }{2}=\pi$ .

Bài 1.20 trang 18 SBT Toán 11 Tập 1: Với giá trị nào của x, mỗi đẳng thức sau đúng?

a) tan x cot x = 1;

b) 1 + tan² x = $\frac{1}{{\cos }^{2}x}$ ;

c) 1 + cot² x = $\frac{1}{{\sin }^{2}x}$ ;

d) tan x + cot x = $\frac{2}{\sin 2x}$ .

Lời giải:

a) Đẳng thức tan x cot x = 1 đúng với mọi x khi tan x và cot x có nghĩa, tức là

⇔ 2sin x cos x ≠ 0 ⇔ sin2x ≠ 0 ⇔ 2x ≠ kπ (k ∈ ℤ) $\iff x\ne k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$ .

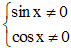
b) Đẳng thức 1 + tan² x = $\frac{1}{{\cos }^{2}x}$  đúng với mọi x khi cos x ≠ 0, tức là x ≠ $\frac{\pi }{2}$  + kπ (k ∈ ℤ).

c) Đẳng thức 1 + cot² x = $\frac{1}{{\sin }^{2}x}$  đúng với mọi x khi sinx ≠ 0, tức là x ≠ kπ (k ∈ ℤ). 

d) Đẳng thức tan x + cot x = $\frac{2}{\sin 2x}$  đúng với mọi x khi

⇔ 2sin x cos x ≠ 0 ⇔ sin2x ≠ 0 ⇔ 2x ≠ kπ (k ∈ ℤ) 

$\iff x\ne k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$ .

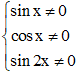
Bài 1.21 trang 18 SBT Toán 11 Tập 1: Từ đồ thị hàm số y = cos x, hãy vẽ các đồ thị hàm số sau:

a) y = – cos x;

b) y = |cos x|;

c) y = cos x + 1;

d) $y=\cos \left(x+\frac{\pi }{2}\right)$ .

Lời giải:

a) Lấy đối xứng đồ thị hàm số y = cos x qua trục hoành ta được đồ thị hàm số y = – cos x.

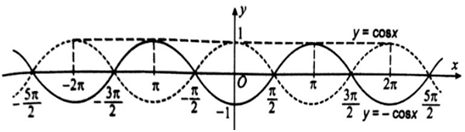
Trong hình trên, đồ thị hàm số y = cos x là đường nét đứt còn đồ thị hàm số y = – cos x là đường nét liền.

b) Ta có 

Từ đó, để vẽ đồ thị hàm số y = |cos x| đầu tiên ta vẽ đồ thị hàm số y = cos x, sau đó giữ nguyên phần đồ thị hàm số y = cos x ở phía trên trục Ox và lấy đối xứng qua trục Ox phần đồ thị hàm số y = cos x ở phía dưới trục Ox.

Trong hình dưới đây, đồ thị hàm số y = |cos x| là đường nét liền.

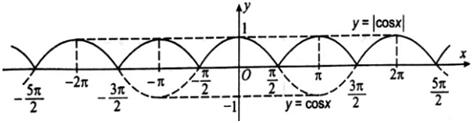
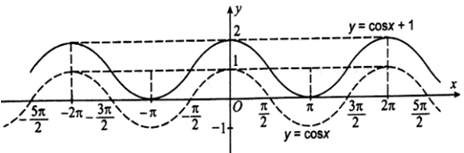
c) Để vẽ đồ thị hàm số y = cos x + 1, đầu tiên ta vẽ đồ thị hàm số y = cos x, sau đó dịch chuyển đồ thị này dọc theo trục Oy lên phía trên 1 đơn vị, ta được đồ thị hàm số y = cosx + 1. Trong hình dưới đây, đồ thị hàm số y = cos x + 1 là đường nét liền.

d) Để vẽ đồ thị hàm số $y=\cos \left(x+\frac{\pi }{2}\right)$  đầu tiên ta vẽ đồ thị hàm số y = cos x, sau đó dịch chuyển đồ thị này dọc theo trục Ox sang bên trái $\frac{\pi }{2}$  đơn vị ta sẽ được đồ thị hàm số $y=\cos \left(x+\frac{\pi }{2}\right)$ . Trong hình vẽ dưới đây đồ thị hàm số $y=\cos \left(x+\frac{\pi }{2}\right)$  là đường nét liền.

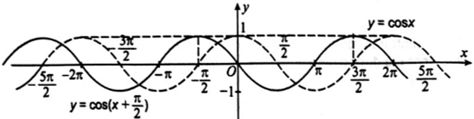
Chú ý rằng $\cos \left(x+\frac{\pi }{2}\right)=-\sin x$  nên đồ thị hàm số $y=\cos \left(x+\frac{\pi }{2}\right)$  cũng có thể có được bằng cách lấy đối xứng đồ thị hàm số y = sin x qua trục Ox.

Bài 1.22 trang 18 SBT Toán 11 Tập 1: Từ đồ thị hàm số y = sin x, hãy xác định các giá trị của x trên đoạn   sao cho:

a) sin x = 0;                                       b) sin x > 0. 

Lời giải:

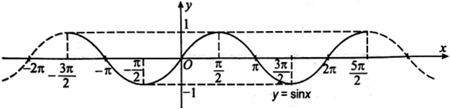
a) Trên đoạn 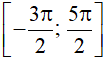, đồ thị hàm số y = sinx cắt trục Ox tại bốn điểm x = − π, x = 0, x = π và x = 2π. Suy ra có bốn giá trị của x để sin x = 0 trên đoạn  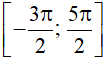 là x = − π, x = 0, x = π và x = 2π.

b) Giải bất phương trình sinx > 0 là tìm những khoảng giá trị của x mà đồ thị hàm số y = sinx nằm phía trên trục Ox. Từ đó, ta được tập nghiệm của bất phương trình sinx > 0 trên đoạn 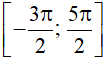  là $S=\left(-\frac{3\pi }{2};-\pi \right)\cup \left(0;\pi \right)\cup \left(2\pi ;\frac{5\pi }{2}\right)$ .

Bài 1.23 trang 18 SBT Toán 11 Tập 1: Một con lắc lò xo dao động điều hoà quanh vị trí cân bằng theo phương trình y = 25 sin 4πt ở đó y được tính bằng centimét còn thời gian t được tính bằng giây.

a) Tìm chu kì dao động của con lắc lò xo.

b) Tìm tần số dao động của con lắc, tức là số lần dao động trong một giây.

c) Tìm khoảng cách giữa điểm cao nhất và thấp nhất của con lắc.

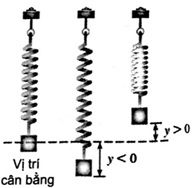
Lời giải:

a) Hàm số y = 25 sin 4πt tuần hoàn với chu kì T = $\frac{2\pi }{4\pi }=\frac{1}{2}$ .

Suy ra chu kì dao động của con lắc lò xo (tức là khoảng thời gian để con lắc thực hiện được một dao động toàn phần) là T = $\frac{1}{2}$  giây.

b) Vì chu kì dao động của con lắc là T = $\frac{1}{2}$  giây nên trong 1 giây con lắc thực hiện được 2 dao động, tức là tần số dao động của con lắc là $f=\frac{1}{T}$ = 2 Hz.

c) Vì phương trình dao động của con lắc là y = 25 sin 4πt nên biên độ dao động của nó là A = 25 cm. Từ đó suy ra, khoảng cách giữa điểm cao nhất và điểm thấp nhất của con lắc là 2A = 50 cm.

Bài 1.24 trang 19 SBT Toán 11 Tập 1: Hằng ngày, Mặt Trời chiếu sáng, bóng của một toà chung cư cao 40 m in trên mặt đất, độ dài bóng của toà nhà này được tính bằng công thức

ở đó S được tính bằng mét, còn t là số giờ tính từ 6 giờ sáng.

a) Tìm độ dài bóng của toà nhà tại các thời điểm 8 giờ sáng, 12 giờ trưa, 2 giờ chiều và 5 giờ 45 phút chiều.

b) Tại thời điểm nào thì độ dài bóng của toà nhà bằng chiều cao toà nhà?

c) Bóng toà nhà sẽ như thế nào khi thời gian tiến dần đến 6 giờ tối?

Lời giải:

a) - Tại thời điểm 8 giờ sáng ta có t = 8 – 6 = 2. Vậy độ dài bóng của toà nhà tại thời điểm 8 giờ sáng là

- Tại thời điểm 12 giờ trưa ta có t = 12 – 6 = 6. Vậy độ dài bóng của toà nhà tại thời điểm 12 giờ trưa là 

Tại thời điểm 12 giờ trưa, Mặt Trời chiếu thẳng đứng từ trên đầu xuống nên toàn bộ toà nhà được chiếu xuống móng của toà nhà.

- Tại thời điểm 2 giờ chiều ta có t = 14 – 6 = 8. Vậy độ dài bóng của toà nhà tại thời điểm 2 giờ chiều là

- Tại thời điểm 5 giờ 45 chiều tối, ta có t = $\left(17+\frac{3}{4}\right)-6=\frac{39}{4}$. Vậy độ dài bóng của toà nhà tại thời điểm 5 giờ 45 chiều tối là 

b) Độ dài bóng của toà nhà bằng chiều cao tòa nhà khi

S(t) = 40

$\iff \frac{\pi }{12}t=\pm \frac{\pi }{4}+k\pi \left(k\in \mathbb{Z}\right)$⇔ t = ±3 + 12k (k ∈ ℤ).

Vì 0 ≤ t ≤ 12 nên t = 3 hoặc t = 9, tức là tại thời điểm 9 giờ sáng hoặc 3 giờ chiều thì bóng của toà nhà dài bằng chiều cao của toà nhà.

c) Khi thời gian tiến dần đến 6 giờ tối thì t → 12, vì vậy $\frac{\pi }{12}t\to \pi$, do đó $\cos \frac{\pi }{12}t\to -\infty$.

Như vậy, bóng của toà nhà sẽ tiến ra vô cùng.