Với Giải Bài 26 trang 18 SBT Toán 8 Tập 1 trong Bài 4: Luyện tập hằng đẳng thức vào phân tích đa thức thành nhân tử Sách bài tập Toán lớp 8 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán lớp 8.
Cho tam giác ABC có cạnh BC = 2x (dm), đường cao AH = x (dm) với x > 0
Bài 26 trang 18 SBT Toán 8 Tập 1: Cho tam giác ABC có cạnh BC = 2x (dm), đường cao AH = x (dm) với x > 0 và hình vuông MNPQ có cạnh MN = y (dm) với y > 0 (Hình 4).
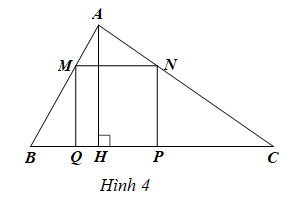
a) Viết công thức tính tổng diện tích của các tam giác AMN, BMQ, CNPdưới dạng tích.
b) Tính tổng diện tích của các tam giác AMN, BMQ, CNP, biết x ‒ y = 2và x + y = 10.
Lời giải:
a) Diện tích của tam giác ABC là:
(dm2)
Diện tích hình vuông MNPQ là:
MN2 = y2 (dm2)
Vì vậy, tổng diện tích của các tam giác AMN, BMQ, CNP là:
S = x2 ‒ y2 (dm2)
b) Từ câu a, ta có
S = x2 ‒ y2 = (x ‒ y)(x + y)
Thay x – y = 2 và x + y = 10 vào S ta được:
S = 2.10 = 20 (dm2).
Vậy tổng diện tích của các tam giác AMN, BMQ, CNP là20 dm2.
Xem thêm các bài giải sách bài tập Toán lớp 8 Cánh diều hay, chi tiết khác:
Bài 22 trang 17 SBT Toán 8 Tập 1: Phân tích mỗi đa thức sau thành nhân tử: a) ;
Bài 23 trang 17 SBT Toán 8 Tập 1: Phân tích mỗi đa thức sau thành nhân tử: a) x3(13xy ‒ 5) ‒ y3(5 ‒ 13xy);
Bài 24 trang 18 SBT Toán 8 Tập 1: Tính giá trị của mỗi biểu thức sau: a) biết .
Xem thêm các bài giải sách bài tập Toán lớp 8 Cánh diều hay, chi tiết khác:
Bài 3: Hằng đẳng thức đáng nhớ
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
