Toptailieu.vn biên soạn và giới thiệu lời giải SBT Toán 8 (Cánh diều) Bài 1: Phân thức đại số hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi vở bài tập Toán 8 Bài 1 từ đó học tốt môn Toán 8.

SBT Toán 8 (Cánh diều) Bài 1: Phân thức đại số

Bài 1 trang 33 SBT Toán 8 Tập 1: Viết điều kiện xác định của mỗi phân thức sau:

a) $\frac{3}{2x\left(5-x\right)}$

b) $\frac{4x}{x^2-4}$

c) $\frac{x}{y^2+2xy}$

d) $\frac{6,4y}{0,4x^2+0,4x}$

Lời giải:

a) Điều kiện xác định của phân thức $\frac{3}{2x\left(5-x\right)}$ là: $2x\left(5-x\right)\ne 0$

b) Điều kiện xác định của phân thức $\frac{4x}{x^2-4}$ là: $x^2-4\ne 0$

c) Điều kiện xác định của phân thức $\frac{x}{y^2+2xy}$ là: $y^2+2xy\ne 0$

d) Điều kiện xác định của phân thức $\frac{6,4y}{0,4x^2+0,4x}$ là: $0,4x^2+0,4x\ne 0$

Bài 2 trang 33 SBT Toán 8 Tập 1: Dùng định nghĩa hai phân thức bằng nhau, hãy giải thích vì sao có thể viết:

a) $\frac{x^2{y}^3}{2x^2{y}^2}=\frac{y}{2}$

b) $\frac{x^2-x-2}{x+1}=\frac{x^2-3x+2}{x-1}$

c) $\frac{x^2-3x+9}{x^3+27}=\frac{1}{x+3}$

Lời giải:

a) Ta có: $x^2{y}^3.2=2x^2{y}^3$ và $2x^2{y}^2.y=2x^2{y}^3$ nên $x^2{y}^3.2=2x^2{y}^2.y$

Vậy $\frac{x^2{y}^3}{2x^2{y}^2}=\frac{y}{2}$

b) Ta có: 

$$\begin{gathered} \left(x^2-x-2\right)\left(x-1\right)=x^3-x^2-2x-x^2+x+2 \\ =x^3-2x^2-x+2 \end{gathered}$$

và 

$$\begin{gathered} \left(x+1\right)\left(x^2-3x+2\right)=x^3-3x^2+2x+x^2-3x+2 \\ =x^3-2x^2-x+2 \end{gathered}$$

Vậy $\frac{x^2-x-2}{x+1}=\frac{x^2-3x+2}{x-1}$

c) Ta có: 

$$\begin{gathered} \left(x^2-3x+9\right)\left(x+3\right)=x^3-3x^2+9x+3x^2-9x+27 \\ =x^3+27 \end{gathered}$$

$\left(x^3+27\right).1=x^3+27$

Vậy $\frac{x^2-3x+9}{x^3+27}=\frac{1}{x+3}$.

Bài 3 trang 33 SBT Toán 8 Tập 1: Mỗi cặp phân thức sau có bằng nhau không? Vì sao?

a) $\frac{x}{5x+5}$ và $\frac{1}{5}$

b) $\frac{-x}{x-5}$ và $\frac{-x\left(x-5\right)}{{\left(x-5\right)}^2}$

c) $\frac{-5}{-x-y}$ và $\frac{5}{x+y}$

d) $\frac{-x}{{\left(x-3\right)}^2}$ và $\frac{x}{{\left(3-x\right)}^2}$

Lời giải:

a) Ta có: $x.5=5x$ và $\left(5x+5\right).1=5x+5$

Do $x.5\ne \left(5x+5\right).1$ nên hai phân thức $\frac{x}{5x+5}$ và $\frac{1}{5}$ không bằng nhau.

b) Ta có: $-x.{\left(x-5\right)}^2=-x{\left(x-5\right)}^2$ và $\left(x-5\right).\left[-x\left(x-5\right)\right]=-x{\left(x-5\right)}^2$

nên $-x.{\left(x-5\right)}^2=\left(x-5\right).\left[-x\left(x-5\right)\right]$

Vậy $\frac{-x}{x-5}=\frac{-x\left(x-5\right)}{{\left(x-5\right)}^2}$

c) Ta có: $-5.\left(x+y\right)=-5\left(x+y\right)$ và $\left(-x-y\right).5=-5\left(x+y\right)$

nên $-5.\left(x+y\right)=\left(-x-y\right).5$

Vậy $\frac{-5}{-x-y}=\frac{5}{x+y}$

d) Ta có: $-x.{\left(3-x\right)}^2=-x{\left(x-3\right)}^2$ và ${\left(x-3\right)}^2.x=x{\left(x-3\right)}^2$

Do $-x{\left(x-3\right)}^2\ne x{\left(x-3\right)}^2$ nên khi $x\ne 0$ và $x\ne 3$ thì hai phân thức $\frac{-x}{{\left(x-3\right)}^2}$ và $\frac{x}{{\left(3-x\right)}^2}$ không bằng nhau

Bài 4 trang 33 SBT Toán 8 Tập 1: Rút gọn mỗi phân thức sau:

a) $\frac{25x^2{y}^3}{35x^3{y}^2}$

b) $\frac{x-y}{y-x}$

c) $\frac{{\left(-x\right)}^5{y}^2}{x^2{\left(-y\right)}^3}$

d) $\frac{x^2-2x}{x^3-4x^2+4x}$

Lời giải:

a) Điều kiện xác định của phân thức là $x\ne 0;y\ne 0$

Ta có: $\frac{25x^2{y}^3}{35x^3{y}^2}=\frac{5.5x^2{y}^3}{5.7x^3{x}^2}=\frac{5y}{7x}$

b) Điều kiện xác định của phân thức là $y-x\ne 0$

Ta có: $\frac{x-y}{y-x}=\frac{-\left(y-x\right)}{y-x}=-1$

c) Điều kiện xác định của phân thức là $x\ne 0;y\ne 0$

Ta có: $\frac{{\left(-x\right)}^5{y}^2}{x^2{\left(-y\right)}^3}=\frac{\left(-1\right).x^5{y}^2}{\left(-1\right).x^2{y}^3}=\frac{x^3}{y}$

d) Điều kiện xác định của phân thức là $x^3-4x^2+4x\ne 0$

Ta có: $\frac{x^2-2x}{x^3-4x^2+4x}=\frac{x\left(x-2\right)}{x\left(x^2-4x+4\right)}=\frac{x\left(x-2\right)}{x{\left(x-2\right)}^2}=\frac{1}{x-2}$

Bài 5 trang 33 SBT Toán 8 Tập 1: Tính giá trị của biểu thức:

a) $A=\frac{x^5{y}^2}{{\left(xy\right)}^3}$ tại $x=1;y=2$

b) $B=\frac{-4\left(x-2\right)x^2}{20\left(2-x\right)y^2}$ tại $x=\frac{1}{2};y=\frac{1}{5}$.

c) $C=\frac{x^2-8x+7}{x^2-1}$ tại $x=-7$

d) $D=\frac{5x^2-10xy+5y^2}{x^2-y^1}$ tại $x=0,5;y=0,6$.

Lời giải:

a) Rút gọn biểu thức: $A=\frac{x^5{y}^2}{{\left(xy\right)}^3}=\frac{x^5{y}^2}{x^3{y}^3}=\frac{x^2}{y}$

ĐKXĐ: ${\left(xy\right)}^3\ne 0$

Giá trị của $A$ khi $x=1;y=2$ là: $\frac{1^2}{2}=\frac{1}{2}$

b) Rút gọn biểu thức: $B=\frac{-4\left(x-2\right)x^2}{20\left(2-x\right)y^2}=\frac{-4.-\left(2-x\right)x^2}{20.\left(2-x\right)y^2}=\frac{x^2}{5y^2}$

ĐKXĐ: $20\left(2-x\right)y^2\ne 0$

Giá trị của $A$ khi $x=\frac{1}{2};y=\frac{1}{5}$ là: $\frac{{\left(\frac{1}{2}\right)}^2}{5.{\left(\frac{1}{5}\right)}^2}=\frac{5}{4}$

c) Rút gọn biểu thức: $C=\frac{x^2-8x+7}{x^2-1}=\frac{\left(x-7\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{x-7}{x+1}$

ĐKXĐ: $x^2-1\ne 0$

Giá trị của $C$ khi $x=-7$ là: $\frac{\left(-7-7\right)}{\left(-7-1\right)}=\frac{7}{4}$

d) Rút gọn biểu thức: 

$$\begin{gathered} D=\frac{5x^2-10xy+5y^2}{x^2-y^2} \\ =\frac{5\left(x^2-2xy+y^2\right)}{\left(x-y\right)\left(x+y\right)} \\ =\frac{5{\left(x-y\right)}^2}{\left(x-y\right)\left(x+y\right)}=\frac{5\left(x-y\right)}{\left(x+y\right)} \end{gathered}$$

ĐKXĐ: $x^2+y^2\ne 0$

Giá trị của $D$ khi $x=0,5;y=0,6$ là: $\frac{5\left(0,5-0,6\right)}{\left(0,5+0,6\right)}=-\frac{5}{11}$

Bài 6 trang 34 SBT Toán 8 Tập 1: Quy đồng mẫu thức các phân thức trong mỗi trường hợp sau:

a) $\frac{2}{15x^3{y}^2};\frac{y}{10x^4{z}^3}$ và $\frac{x}{20y^{3}z}$

b) $\frac{x}{2x+6}$ và $\frac{4}{x^2-9}$

c) $\frac{2x}{x^3-1}$ và $\frac{x-1}{x^2+x+1}$

d) $\frac{x}{1+2x+x^2}$ và $\frac{3}{5x^2-5}$

Lời giải:

a) Ta có:

Chọn MTC là: $60x^4{y}^3{z}^3$.

Nhân tử phụ của ba mẫu thức $15x^3{y}^2;10x^4{z}^3;20y^{3}z$ lần lượt là: $4xy{z}^3;6y^3;3x^4{z}^2$

Vậy: $\frac{2}{15x^3{y}^2}=\frac{2\left(4xy{z}^3\right)}{15x^3{y}^2.4xy{z}^3}=\frac{8xy{z}^3}{60x^4{y}^3{z}^3}$

 $\frac{y}{10x^4{z}^3}=\frac{y.6y^3}{10x^4{z}^3}=\frac{6y^4}{60x^4{y}^3{z}^3}$

$\frac{x}{20y^{3}z}=\frac{x.3x^4{z}^2}{20y^{3}z.3x^4{z}^2}=\frac{3x^5{z}^2}{60x^4{y}^3{z}^3}$

b) Ta có: $2x+6=2\left(x+3\right);x^2-9=\left(x+3\right)\left(x-3\right)$

Chọn MTC là: $2\left(x^2-9\right)$

Nhân tử phụ của hai mẫu thức $2x+6;x^2-9$ lần lượt là $\left(x-3\right);2$

Vậy: $\frac{x}{2x+6}=\frac{x\left(x-3\right)}{2\left(x+3\right)\left(x-3\right)}=\frac{x^2-3x}{2\left(x^2-9\right)}$

  $\frac{4}{x^2-9}=\frac{4.2}{2\left(x+3\right)\left(x-3\right)}=\frac{8}{2\left(x^2-9\right)}$

c) Ta có: $x^3-1=\left(x-1\right)\left(x^2+x+1\right)$

Chọn MTC là: $x^3-1$

Nhân tử phụ của hai mẫu thức $x^3-1;x^2+x+1$ lần lượt là: $1;\left(x-1\right)$

Vậy: $\frac{2x}{x^3-1}$

 $\frac{x-1}{x^2+x+1}=\frac{\left(x-1\right)\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{{\left(x-1\right)}^2}{x^3-1}$

d) Ta có: 

$$\begin{gathered} 1+2x+x^2={\left(x+1\right)}^2; \\ 5x^2-5=5\left(x^2-1\right)=5\left(x-1\right)\left(x+1\right) \end{gathered}$$

Chọn MTC là: $5\left(x-1\right){\left(x+1\right)}^2$

Nhân tử phụ của hai mẫu thức $1+2x+x^2;5x^2-5$ lần lượt là: $5\left(x-1\right);x+1$

Vậy: $\frac{x}{1+2x+x^2}=\frac{x.5.\left(x-1\right)}{5\left(x-1\right){\left(x+1\right)}^2}=\frac{5x\left(x-1\right)}{5\left(x-1\right){\left(x+1\right)}^2}$

          $\frac{3}{5x^2-5}=\frac{3\left(x+1\right)}{5\left(x-1\right){\left(x+1\right)}^2}$

Bài 7 trang 34 SBT Toán 8 Tập 1: Chứng tỏ giá trị của biểu thức sau không phụ thuộc vào giá trị của biến (với $a$ là một số):

a) $\frac{x^2-y^2}{\left(x+y\right)\left(ax-ay\right)}\left(a\ne 0\right)$

b) $\frac{{\left(x+a\right)}^2-x^2}{2x+a}$

Lời giải:

a) Ta có: $\frac{x^2-y^2}{\left(x+y\right)\left(ax-ay\right)}=\frac{\left(x-y\right)\left(x+y\right)}{\left(x+y\right).a\left(x-y\right)}=\frac{1}{a}$

Vậy biểu thức đã cho không phụ thuộc vào giá trị của biến.

b) Ta có: $\frac{{\left(x+a\right)}^2-x^2}{2x+a}=\frac{\left(x+a-x\right)\left(x+a+x\right)}{2x+a}=\frac{a\left(2x+a\right)}{2x+a}=a$

Vậy biểu thức đã cho không phụ thuộc vào giá trị của biến.

Bài 8 trang 34 SBT Toán 8 Tập 1: Một miếng bìa có dạng hình vuông với độ dài xạnh là $x$ (cm). Người ta cắt đi ở mỗi góc của miếng bìa một hình vuông sao cho bốn hình vuông bị cắt đi có cùng độ dài cạnh là $y$ (cm) với $0<2y<x$ (Hình 2).

a) Viết phân thức biểu thị tỉ số diện tích của miếng bìa ban đầu và phần miếng bìa còn lại sau khi bị cắt.

b) Tính giá trị của phân thức đó tại $x=4;y=1$

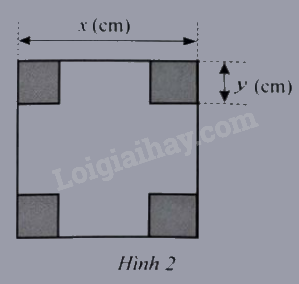
Lời giải:

a) Diện tích của miếng bìa ban đầu là: $x^2\left(c{m}^2\right)$

Diện tích của phần bìa còn lại sau khi cắt là: $x^2-4y^2\left(c{m}^2\right)$

Phân thức biểu thị tỉ số diện tích của miếng bìa ban đầu và phần miếng bìa còn lại sau khi bị cắt là: $\frac{x^2}{x^2-4y^2}$

b) Giá trị của phân thức $\frac{x^2}{x^2-4y^2}$ tại $x=4;y=1$ là: $\frac{4^2}{4^2-{4.1}^2}=\frac{4}{3}$

Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:

Bài tập cuối chương 1

Bài 2: Phép cộng, phép trừ phân thức đại số

Bài 3: Phép nhân, phép chia phân thức đại số

Bài tập cuối chương 2

Bài 1: Hàm số