Toptailieu.vn giới thiệu Giải bài tập Toán lớp 10 Bài 4. Các số đặc trưng đo mức độ phân tán của mẫu số liệu sách Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10 Tập 1. Mời các bạn đón xem:

Toán 10 Chân trời sáng tạo Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

1. KHOẢNG BIẾN THIÊN VÀ KHOẢNG TỨ PHÂN VỊ

Câu hỏi trang 120 Toán 10

HĐ Khởi động trang 120 Toán 10 Tập 1: Nhiệt độ trung bình các tháng trong năm 2019 tại Lai Châu và Lâm Đồng

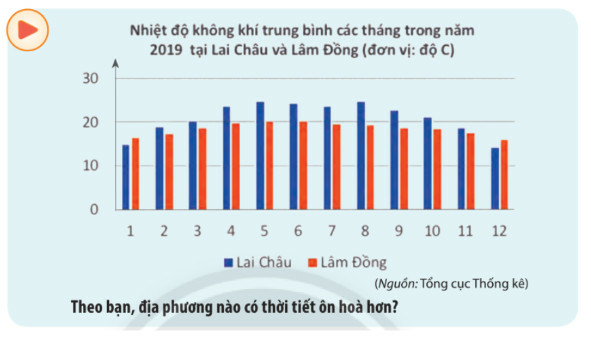
Lời giải 

Nếu so sánh nhiệt độ trung bình thì 2 địa phương đều có thời tiết ôn hòa dễ chịu. Tuy nhiên so sánh sự chên lệch nhiệt độ giữa các tháng thì Lâm Đồng có thời tiết ôn hòa hơn do tháng thấp nhất là khoảng 15 độ (cao hơn Lai Châu) và sự chênh lệch nhiệt độ giữa các tháng không lớn (khoảng 4 độ C).

HĐ Khám phá 1 trang 120 Toán 10 Tập 1: Thời gian hoàn thành bài chạy 5 km (tính theo phút) của hai nhóm thanh niên được cho ở bảng sau:

a) Hãy tính độ chênh lệch giữa thời gian chạy của người nhanh nhất và người chậm nhất trong từng nhóm.

b) Nhóm nào có thành tích chạy đồng đều hơn?

Phương pháp giải:

a) Độ chênh lệch giữa thời gian chạy của người nhanh nhất và người chậm nhất trong nhóm 1 là:

$47-17=30$ (phút)

Độ chênh lệch giữa thời gian chạy của người nhanh nhất và người chậm nhất trong nhóm 2 là:

$32-29=3$(phút)

b) Dễ thấy: nhóm 2 có thành tích chạy đồng đều hơn.

Câu hỏi trang 121 Toán 10

Thực hành 1 trang 121 Toán 10 Tập 1: Hãy tìm khoảng biến thiên và khoảng tứ phân vị của các mẫu số liệu sau:

a) $10;13;15;2;10;19;2;5;7$

b) $15;19;10;5;9;10;1;2;5;15$

Phương pháp giải:

Cho mẫu số liệu: $x_1,x_2,...,x_n$

Sắp xếp mẫu số liệu theo thứ tự không giảm: $X_1,X_2,...,X_n$

+) Khoảng biến thiên: $R=X_n-X_1$

+) Tứ phân vị: $Q_1,Q_2,Q_3$

Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: $X_1,X_2,...,X_n$

Bước 2: $Q_2=M_e=\{\begin{array}{l}{X}_{k+1}(n=2k+1)\\ \frac{1}{2}(X_k+X_{k+1})(n=2k)\end{array}$

$Q_1$ là trung vị của nửa số liệu đã sắp xếp bên trái $Q_2$ (không bao gồm $Q_2$ nếu n lẻ)

$Q_3$ là trung vị của nửa số liệu đã sắp xếp bên phải $Q_2$ (không bao gồm $Q_2$ nếu n lẻ)

Khoảng tứ phân vị: ${\mathrm{\Delta }}_Q=Q_3-Q_1$

Lời giải 

a) Xét mẫu số liệu đã sắp xếp là: $2;2;5;7;10;10;13;15;19$

Khoảng biến thiên của mẫu số liệu là: $R=19-2=17.$

Cỡ mẫu là $n=9$ là số lẻ nên giá trị tứ phân vị thứ hai là: $Q_2=10.$

Tứ phân vị thứ nhất là trung vị của mẫu: $2;2;5;7$. Do đó $Q_1=3,5$

Tứ phân vị thứ ba là trung vị của mẫu: $10;13;15;19$. Do đó $Q_3=14$

Khoảng tứ phân vị của mẫu là: ${\mathrm{\Delta }}_Q=14-3,5=10,5$

b) Xét mẫu số liệu đã sắp xếp là: $1;2;5;5;9;10;10;15;15;19$

Khoảng biến thiên của mẫu số liệu là: $R=19-1=18.$

Cỡ mẫu là $n=10$ là số chẵn nên giá trị tứ phân vị thứ hai là: $Q_2=9,5.$

Tứ phân vị thứ nhất là trung vị của mẫu: $1;2;5;5;9$. Do đó $Q_1=5.$

Tứ phân vị thứ ba là trung vị của mẫu: $10;10;15;15;19$. Do đó $Q_3=15$

Khoảng tứ phân vị của mẫu là: ${\mathrm{\Delta }}_Q=15-5=10$

Vận dụng 1 trang 121 Toán 10 Tập 1: Dưới đây là bảng số liệu thống kê của Biểu đồ nhiệt trung bình các tháng trong 2019 của hai tình Lai Châu và Lâm Đồng (được đề cập đến ở hoạt động khởi động của bài học)

a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của nhiệt độ trung bình mỗi tháng của tỉnh Lai Châu và Lâm đồng.

b) Hãy cho biết trong một năm, nhiệt độ ở địa phương nào ít thay đổi hơn.

Phương pháp giải:

a) Cho mẫu số liệu: $x_1,x_2,...,x_n$

Sắp xếp mẫu số liệu theo thứ tự không giảm: $X_1,X_2,...,X_n$

+) Khoảng biến thiên: $R=X_n-X_1$

+) Tứ phân vị: $Q_1,Q_2,Q_3$

Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: $X_1,X_2,...,X_n$

Bước 2: $Q_2=M_e=\{\begin{array}{l}{X}_{k+1}(n=2k+1)\\ \frac{1}{2}(X_k+X_{k+1})(n=2k)\end{array}$

$Q_1$ là trung vị của nửa số liệu đã sắp xếp bên trái $Q_2$ (không bao gồm $Q_2$ nếu n lẻ)

$Q_3$ là trung vị của nửa số liệu đã sắp xếp bên phải $Q_2$ (không bao gồm $Q_2$ nếu n lẻ)

Khoảng tứ phân vị: ${\mathrm{\Delta }}_Q=Q_3-Q_1$

b) So sánh khoảng biến thiên

Lời giải 

a)

+) Tỉnh Lai Châu: Xét mẫu số liệu đã sắp xếp là:

$\begin{array}{cccccccccccc}14,2& 14,8& 18,6& 18,8& 20,3& 21,0& 22,7& 23,5& 23,6& 24,2& 24,6& 24,7\end{array}$

 Khoảng biến thiên của mẫu số liệu là: $R=24,7-14,2=10,5.$

Cỡ mẫu là $n=12$ là số chẵn nên giá trị tứ phân vị thứ hai là: $Q_2=21,85.$

Tứ phân vị thứ nhất là trung vị của mẫu: $\begin{array}{cccccc}14,2& 14,8& 18,6& 18,8& 20,3& 21,0\end{array}$. Do đó $Q_1=18,7.$

Tứ phân vị thứ ba là trung vị của mẫu: $\begin{array}{cccccc}22,7& 23,5& 23,6& 24,2& 24,6& 24,7\end{array}$. Do đó $Q_3=23,9$

Khoảng tứ phân vị của mẫu là: ${\mathrm{\Delta }}_Q=23,9-18,7=5,2$

+) Tỉnh Lâm Đổng: Xét mẫu số liệu đã sắp xếp là:

$16,016,317,417,518,518,618,719,319,519,820,220,3$

Khoảng biến thiên của mẫu số liệu là: $R=20,3-16,0=4,3.$

Cỡ mẫu là $n=12$ là số chẵn nên giá trị tứ phân vị thứ hai là: $Q_2=18,65.$

Tứ phân vị thứ nhất là trung vị của mẫu: $\begin{array}{cccccc}16,0& 16,3& 17,4& 17,5& 18,5& 18,6\end{array}$. Do đó $Q_1=17,45.$

Tứ phân vị thứ ba là trung vị của mẫu: $\begin{array}{cccccc}18,7& 19,3& 19,5& 19,8& 20,2& 20,3\end{array}$. Do đó $Q_3=19,65$

Khoảng tứ phân vị của mẫu là: ${\mathrm{\Delta }}_Q=19,65-17,45=2,2$

Câu hỏi trang 122 Toán 10

Thực hành 2 trang 122 Toán 10 Tập 1: Hãy tìm giá trị ngoại lệ của mẫu số liệu: 37; 12; 3; 9; 10; 9; 12; 3; 10.

Phương pháp giải:

Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: $X_1,X_2,...,X_n$

Bước 2: $Q_2=M_e=\{\begin{array}{l}{X}_{k+1}(n=2k+1)\\ \frac{1}{2}(X_k+X_{k+1})(n=2k)\end{array}$

$Q_1$ là trung vị của nửa số liệu đã sắp xếp bên trái $Q_2$ (không bao gồm $Q_2$ nếu n lẻ)

$Q_3$ là trung vị của nửa số liệu đã sắp xếp bên phải $Q_2$ (không bao gồm $Q_2$ nếu n lẻ)

Khoảng tứ phân vị: ${\mathrm{\Delta }}_Q=Q_3-Q_1$

Bước 3: Tìm x trong mẫu sao cho $x>Q_3+1,5{\mathrm{\Delta }}_Q$ hoặc $x<Q_1-1,5{\mathrm{\Delta }}_Q$

Lời giải 

Xét mẫu số liệu đã sắp xếp là:

$3;3;9;9;10;10;12;12;37.$

Cỡ mẫu là $n=9$ là số lẻ nên giá trị tứ phân vị thứ hai là: $Q_2=10.$

Tứ phân vị thứ nhất là trung vị của mẫu: $3;3;9;9.$. Do đó $Q_1=6.$

Tứ phân vị thứ ba là trung vị của mẫu: $10;12;12;37.$. Do đó $Q_3=12$

Khoảng tứ phân vị của mẫu là: ${\mathrm{\Delta }}_Q=12-6=6$

Giá trị ngoại lệ x thỏa mãn $x>12+1,5.6=21$ hoặc $x<6-1,5.6=-3$.

Vậy giá trị ngoại lệ của mẫu số liệu đó là $37$.

2. PHƯƠNG SAI VÀ ĐỘ LỆCH CHUẨN 

HĐ Khám phá 2 trang 122 Toán 10 Tập 1: Hai cung thủ A và B đã ghi lại kết quả từng lần bắn của mình ở bảng sau:

a) Tính kết quả trung bình của mỗi cung thủ trên

b) Cung thủ nào có kết quả các lần bắn ổn định hơn?

Lời giải 

a) Kết quả trung bình của Cung thủ A là:

$\frac{8+9+10+7+6+10+6+7+9+8}{10}=8$

Kết quả trung bình của Cung thủ A là:

$\frac{10+6+8+7+9+9+8+7+8+8}{10}=8$

b)

+) Khoảng biến thiên số điểm của cung thủ A là: $R=10-6=4$

Xét mẫu số liệu đã sắp xếp là:

$\begin{array}{cccccccccc}6& 6& 7& 7& 8& 8& 9& 9& 10& 10\end{array}$

Cỡ mẫu là $n=10$ là số chẵn nên giá trị tứ phân vị thứ hai là: $Q_2=8.$

Tứ phân vị thứ nhất là trung vị của mẫu:$6,6,7,7,8$. Do đó $Q_1=7.$

Tứ phân vị thứ ba là trung vị của mẫu: $8,9,9,10,10$. Do đó $Q_3=9$

Khoảng tứ phân vị của mẫu là: ${\mathrm{\Delta }}_Q=9-7=2$

+) Khoảng biến thiên số điểm của cung thủ A là: $R=10-6=4$

Xét mẫu số liệu đã sắp xếp là:

$\begin{array}{cccccccccc}6& 7& 7& 8& 8& 8& 8& 9& 9& 10\end{array}$

Cỡ mẫu là $n=10$ là số chẵn nên giá trị tứ phân vị thứ hai là: $Q_2=8.$

Tứ phân vị thứ nhất là trung vị của mẫu:$6,6,7,7,8$. Do đó $Q_1=7.$

Tứ phân vị thứ ba là trung vị của mẫu: $8,9,9,10,10$. Do đó $Q_3=9$

Khoảng tứ phân vị của mẫu là: ${\mathrm{\Delta }}_Q=9-7=2$

=> Nếu so sánh khoảng chênh lệch và khoảng tứ phân vị thì không xác định được kết quả của cung thủ nào ổn định hơn.

Câu hỏi trang 124 Toán 10

Vận dụng 2 trang 124 Toán 10 Tập 1: Bảng dưới đây thống kê tổng số giờ nắng trong năm 2019 theo từng tháng được đo bởi hai trạm quan sát khí tượng đặt ở Tuyên Quang và Cà Mau.

a) Hãy tính phương sai và độ lệch chuẩn của dữ liệu từng tỉnh.

b) Nêu nhận xét về sự thay đổi tổng số giờ nắng theo từng tháng ở mỗi tỉnh.

Phương pháp giải:

Cho mẫu số liệu $x_1,x_2,...,x_n.$

Bước 1. Tính số trung bình $\overline{x}=\frac{x_1+x_2+...+x_n}{n}$

Bước 2: +) Tính phương sai $S^2=\frac{1}{n}\left[{\left(x_1-\overline{x}\right)}^2+{\left(x_2-\overline{x}\right)}^2+...+{\left(x_n-\overline{x}\right)}^2\right]$ hoặc $S^2=\frac{1}{n}\left({x_1}^2+{x_2}^2+...+{x_n}^2\right)-{\overline{x}}^2$

              +) Độ lệch chuẩn $S=\sqrt{S^2}$

Lời giải 

+) Tuyên Quang:

Số giờ nắng trung bình $\overline{x}=\frac{25+89+72+117+106+177+156+203+227+146+117+145}{12}=131,67$

Phương sai: $S^2=\frac{1}{12}\left({25}^2+{89}^2+...+{145}^2\right)-131,{67}^2\approx 2921,2$

Độ lệch chuẩn $S=\sqrt{2921,2}\approx 54$

+) Cà Mau:

Số giờ nắng trung bình $\overline{x}=\frac{180+223+257+245+191+111+141+134+130+122+157+173}{12}=172$

Phương sai: $S^2=\frac{1}{12}\left[\left({180}^2+{223}^2+...+{173}^2\right)-{172}^2\right]=2183$

Độ lệch chuẩn $S=\sqrt{2183}=46,7$

=> Nhận xét: Ở Tuyên Quang tổng số giờ nắng theo từng tháng thay đổi nhiều hơn so với ở Cà Mau.

Bài tập

Bài 1 trang 124 Toán 10 Tập 1: Hãy chọn ngẫu nhiên trong lớp ra 5 bạn nam và 5 bạn nữ rồi do chiều cao các bạn đó. So sánh xem chiều cao của các bạn năm hay các bạn nữ đồng đều hơn.

Phương pháp giải

Từ mẫu số liệu so sánh hai giá trị: Khoảng biến thiên hoặc khoảng tứ phân vị.

+ Nếu trong mẫu không có số liệu nào quá lớn hay quá nhỏ => so sánh khoảng biến thiên

+ Nếu trong mẫu có 1 số liệu quá lớn hoặc quá nhỏ => so sánh khoảng tứ phân vị.

Lời giải 

+) Khoảng biến thiên chiều cao của các học sinh nam là: $176-164=12$

+) Tứ phân vị: $Q_1,Q_2,Q_3$

Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: $164,168,170,172,176$

Bước 2: $n=5$, là số lẻ nên $Q_2=M_e=170$

$Q_1$ là trung vị của nửa số liệu $164,168$. Do đó $Q_1=\frac{1}{2}(164+168)=166$

$Q_3$ là trung vị của nửa số liệu $172,176$. Do đó $Q_3=\frac{1}{2}(172+176)=174$

Khoảng tứ phân vị ${\mathrm{\Delta }}_Q=174-166=8$

+) Khoảng biến thiên chiều cao của các học sinh nữ là: $162-152=10$

+) Tứ phân vị: $Q_1,Q_2,Q_3$

Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: $152,155,157,160,162$

Bước 2: $n=5$, là số lẻ nên $Q_2=M_e=157$

$Q_1$ là trung vị của nửa số liệu $152,155$. Do đó $Q_1=\frac{1}{2}(152+155)=153,5$

$Q_3$ là trung vị của nửa số liệu $160,162$. Do đó $Q_3=\frac{1}{2}(160+162)=161$

Khoảng tứ phân vị ${\mathrm{\Delta }}_Q=161-153,5=7,5$

Kết luận: So sánh khoảng biến thiên hay tứ phân vị thì theo mẫu số liệu trên, chiều cao của 5 bạn nữ là đồng đều hơn.

Bài 2 trang 124 Toán 10 Tập 1: Hãy tìm độ lệch chuẩn, khoảng biến thiên, khoảng tứ phân vị và các giá trị ngoại lệ của các mẫu số liệu sau:

a) 6; 8; 3; 4; 5; 6; 7; 2; 4.

b) 13; 37; 64; 12; 26; 43; 29; 23.

Phương pháp giải

Cho mẫu số liệu $x_1,x_2,...,x_n.$

+) số trung bình $\overline{x}=\frac{x_1+x_2+...+x_n}{n}$

+) phương sai $S^2=\frac{1}{n}\left[{\left(x_1-\overline{x}\right)}^2+{\left(x_2-\overline{x}\right)}^2+...+{\left(x_n-\overline{x}\right)}^2\right]$ hoặc $S^2=\frac{1}{n}\left({x_1}^2+{x_2}^2+...+{x_n}^2\right)-{\overline{x}}^2$

 => Độ lệch chuẩn $S=\sqrt{S^2}$

Sắp xếp mẫu số liệu theo thứ tự không giảm: $X_1,X_2,...,X_n$

+) Khoảng biến thiên: $R=X_n-X_1$

Tứ phân vị: $Q_1,Q_2,Q_3$

Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: $X_1,X_2,...,X_n$

Bước 2: $Q_2=M_e=\{\begin{array}{l}{X}_{k+1}(n=2k+1)\\ \frac{1}{2}(X_k+X_{k+1})(n=2k)\end{array}$

$Q_1$ là trung vị của nửa số liệu đã sắp xếp bên trái $Q_2$ (không bao gồm $Q_2$ nếu n lẻ)

$Q_3$ là trung vị của nửa số liệu đã sắp xếp bên phải $Q_2$ (không bao gồm $Q_2$ nếu n lẻ)

+) Khoảng tứ phân vị: ${\mathrm{\Delta }}_Q=Q_3-Q_1$

+) x là giá trị ngoại lệ trong mẫu nếu $x>Q_3+1,5{\mathrm{\Delta }}_Q$ hoặc $x<Q_1-1,5{\mathrm{\Delta }}_Q$

Lời giải 

a)

+) Số trung bình $\overline{x}=\frac{6+8+3+4+5+6+7+2+4}{9}=5$

+) phương sai hoặc $S^2=\frac{1}{9}\left(6^2+8^2+...+4^2\right)-5^2=\frac{10}{3}$

  => Độ lệch chuẩn $S=\sqrt{\frac{10}{3}}\approx 1,8$

Sắp xếp mẫu số liệu theo thứ tự không giảm: 2; 3; 4; 4; 5; 6; 6; 7; 8.

+) Khoảng biến thiên: $R=8-2=6$

Tứ phân vị: $Q_1,Q_2,Q_3$

$Q_2=M_e=5$

$Q_1$ là trung vị của nửa số liệu 2; 3; 4; 4. Do đó $Q_1=3,5$

$Q_3$ là trung vị của nửa số liệu: 6; 6; 7; 8. Do đó $Q_3=6,5$

+) Khoảng tứ phân vị: ${\mathrm{\Delta }}_Q=6,5-3,5=3$

+) x là giá trị ngoại lệ trong mẫu nếu $x>6,5+1,5.3=11$ hoặc $x<3,5-1,5.3=-1$

Vậy không có giá trị ngoại lệ trong mẫu số liệu trên.

b)

+) Số trung bình $\overline{x}=\frac{13+37+64+12+26+43+29+23}{8}=30,875$

+) phương sai hoặc $S^2=\frac{1}{8}\left({13}^2+{37}^2+...+{23}^2\right)-30,{875}^2\approx 255,8$

  => Độ lệch chuẩn $S\approx 16$

Sắp xếp mẫu số liệu theo thứ tự không giảm: 12; 13; 23; 26; 29; 37; 43; 64.

+) Khoảng biến thiên: $R=64-12=52$

Tứ phân vị: $Q_1,Q_2,Q_3$

$Q_2=M_e=27,5$

$Q_1$ là trung vị của nửa số liệu 12; 13; 23; 26. Do đó $Q_1=18$

$Q_3$ là trung vị của nửa số liệu: 29; 37; 43; 64. Do đó $Q_3=40$

+) Khoảng tứ phân vị: ${\mathrm{\Delta }}_Q=40-18=22$

+) x là giá trị ngoại lệ trong mẫu nếu $x>40+1,5.22=73$ hoặc $x<18-1,5.22=-15$

Vậy không có giá trị ngoại lệ trong mẫu số liệu trên.

Câu hỏi trang 125 Toán 10

Bài 3 trang 125 Toán 10 Tập 1: Hãy tìm độ lệch chuẩn, khoảng biến thiên, khoảng tứ phân vị của các mẫu số liệu sau:

a)

b)

Cho bảng số liệu:

Phương pháp giải

+) Số trung bình: $\overline{x}=\frac{x_1.f_1+x_2.f_2+...+x_m.f_m}{f_1+f_2+...+f_m}$

+) Phương sai $S^2=\frac{1}{n}\left(f_1.{x_1}^2+f_2..{x_2}^2+...+f_n..{x_n}^2\right)-{\overline{x}}^2$

  => Độ lệch chuẩn $S=\sqrt{S^2}$

Sắp xếp mẫu số liệu theo thứ tự không giảm: $X_1,X_2,...,X_n$

+) Khoảng biến thiên: $R=X_n-X_1$

Tứ phân vị: $Q_1,Q_2,Q_3$

+) Khoảng tứ phân vị: ${\mathrm{\Delta }}_Q=Q_3-Q_1$

Lời giải 

a) +) Số trung bình $\overline{x}=\frac{-2.10+(-1).10+0.30+1.20+2.10}{10+20+30+20+10}=0$

+) phương sai hoặc $S^2=\frac{1}{9}\left(10.{(-2)}^2+10.{(-1)}^2+...+{10.2}^2\right)-0^2\approx 13,33$

  => Độ lệch chuẩn $S\approx 3,65$

+) Khoảng biến thiên: $R=2-(-2)=4$

Tứ phân vị: $Q_2=0;Q_1=-1;Q_3=1$

+) Khoảng tứ phân vị: ${\mathrm{\Delta }}_Q=1-(-1)=2$

b) Giả sử cỡ mẫu $n=10$. Khi đó mẫu số liệu trở thành:

+) Số trung bình $\overline{x}=\frac{0.0,1+1.0,2+2.0,4+3.0,2+4.0,1}{0,1+0,2+0,4+0,2+0,1}=2$

+) phương sai hoặc $S^2=\frac{1}{1}\left(0,{1.0}^2+0,{2.1}^2+...+0,{1.4}^2\right)-2^2=1,2$

  => Độ lệch chuẩn $S\approx 1,1$

+) Khoảng biến thiên: $R=4-0=4$

Tứ phân vị: $Q_2=2;Q_1=1;Q_3=3$

+) Khoảng tứ phân vị: ${\mathrm{\Delta }}_Q=3-1=2$

Bài 4 trang 125 Toán 10 Tập 1: Hãy so sánh số trung bình, phương sai và độ lệch chuẩn của ba mẫu só liệu sau:

Mẫu 1: 0,1;  0,3;  0,5;  0,5;  0,3;  0,7.

Mẫu 2: 1,1;  1, 3;  1,5;  1,5;  1,3; 1,7.

Mẫu 3: 1;       3;     5;     5;       3;    7.

Phương pháp giải

+) số trung bình $\overline{x}=\frac{x_1+x_2+...+x_n}{n}$

+) Phương sai $S^2=\frac{1}{n}\left[{\left(x_1-\overline{x}\right)}^2+{\left(x_2-\overline{x}\right)}^2+...+{\left(x_n-\overline{x}\right)}^2\right]$ hoặc $S^2=\frac{1}{n}\left({x_1}^2+{x_2}^2+...+{x_n}^2\right)-{\overline{x}}^2$

+) Độ lệch chuẩn $S=\sqrt{S^2}$

Lời giải 

Mẫu 1:

+) Số trung bình: $\overline{x}=\frac{0,1+0,3+0,5+0,5+0,3+0,7}{6}=0,4$

+) Phương sai $S^2=\frac{1}{6}\left(0,1^2+0,3^2+0,5^2+0,5^2+0,3^2+0,7^2\right)-0,4^2\approx 0,0367$

+) Độ lệch chuẩn $S=\sqrt{S^2}\approx 0,19$

Mẫu 2:

+) Số trung bình: $\overline{x}=\frac{1,1+1,3+1,5+1,5+1,3+1,7}{6}=1,4$

+) Phương sai $S^2=\frac{1}{6}\left(1,1^2+1,3^2+1,5^2+1,5^2+1,3^2+1,7^2\right)-1,4^2\approx 0,0367$

+) Độ lệch chuẩn $S=\sqrt{S^2}\approx 0,19$

Mẫu 3:

+) Số trung bình: $\overline{x}=\frac{1+3+5+5+3+7}{6}=4$

+) Phương sai $S^2=\frac{1}{6}\left(1^2+3^2+5^2+5^2+3^2+7^2\right)-4^2\approx 3,67$

+) Độ lệch chuẩn $S=\sqrt{S^2}\approx 1,9$

Kết luận:

Số liệu ở mẫu 2 hơn số liệu ở mẫu 1 là 1 đơn vị, số trung bình của mẫu 2 hơn số trung bình mẫu 1 là 1 đơn vị, còn phương sai và độ lệch chuẩn là như nhau.

Số liệu ở mẫu 3 gấp 10 lần số liệu mẫu 1, số trung bình, phương sai và độ lệch chuẩn của mẫu 3 lần lượt gấp 10 lần, 100 lần và 10 lần mẫu 1.

Bài 5 trang 125 Toán 10 Tập 1: Sản lượng lúa các năm từ 2014 đến 2018 của hai tỉnh Thái Bình và Hậu Giang được cho ở bảng sau (đơn vị nghìn tấn):

a) Hãy tính độ lệch chuẩn và khoảng biến thiên của sản lượng lúa từng tỉnh.

b) Tỉnh nào có sản lượng lúa ổn định hơn? Tại sao?

Phương pháp giải

a)

+) Tình độ lệch chuẩn:

Bước 1:  Tìm số trung bình $\overline{x}=\frac{x_1+x_2+...+x_n}{n}$

Bước 2: Tính phương sai $S^2=\frac{1}{n}\left[{\left(x_1-\overline{x}\right)}^2+{\left(x_2-\overline{x}\right)}^2+...+{\left(x_n-\overline{x}\right)}^2\right]$ hoặc $S^2=\frac{1}{n}\left({x_1}^2+{x_2}^2+...+{x_n}^2\right)-{\overline{x}}^2$

=> Độ lệch chuẩn $S=\sqrt{S^2}$

+) Khoảng biến thiên = số liệu lớn nhất – số liệu nhỏ nhất

b)

So sánh khoảng biến thiên và độ lệch chuẩn, tỉnh nào có khoảng biến thiên và độ lệch chuẩn nhỏ hơn thì có sản lượng lúa ổn định hơn.

Lời giải 

a)

Tỉnh Thái Bình:

Số trung bình $\overline{x}=\frac{1061,9+1061,9+1053,6+942,6+1030,4}{5}=1030,08$

Phương sai$S^2=\frac{1}{5}\left(1061,9^2+1061,9^2+1053,6^2+942,6^2+1030,4^2\right)-1030,{08}^2=2046,2$

=> Độ lệch chuẩn $S=\sqrt{S^2}\approx 45,2$

+) Khoảng biến thiên $R=1061,9-942,6=119,3$

Tỉnh Hậu Giang:

Số trung bình $\overline{x}=\frac{1204,6+1293,1+1231,0+1261,0+1246,1}{5}=1247,16$

Phương sai$S^2=\frac{1}{6}\left(1204,6^2+1293,1^2+1231,0^2+1261,0^2+1246,1^2\right)-1247,{16}^2=875,13$

=> Độ lệch chuẩn $S=\sqrt{S^2}\approx 29,6$

+) Khoảng biến thiên $R=1293,1-1204,6=88,5$

b)

So sánh khoảng biến thiên và độ lệch chuẩn ta đều thấy tỉnh Hậu Giang có sản lượng lúa ổn định hơn.

Bài 6 trang 125 Toán 10 Tập 1: Kết quả điều tra mức lương hằng tháng của một số công nhân của hai nhà máy A và B được cho ở bảng sau (đơn vị: triệu đồng):

a) Hãy tìm số trung bình, mốt, tứ phân vị và độ lệch chuẩn của hai mẫu số liệu lấy từ nhà máy A và nhà máy B.

b) Hãy tìm các giá trị ngoại lệ trong mỗi mẫu số liệu trên. Công nhân nhà máy nào có mức lương cao hơn? Tại sao?

Phương pháp giải

a)

+) Số trung bình: $\overline{x}=\frac{x_1+x_2+...+x_n}{n}$

+) Mốt: là giá trị xuất hiện nhiều nhất trong mẫu số liệu.

+) Tứ phân vị: $Q_1,Q_2,Q_3$

Sắp xếp mẫu số liệu theo thứ tự không giảm: $X_1,X_2,...,X_n$

$Q_2=M_e=\{\begin{array}{l}{X}_{k+1}(n=2k+1)\\ \frac{1}{2}(X_k+X_{k+1})(n=2k)\end{array}$

$Q_1$ là trung vị của nửa số liệu đã sắp xếp bên trái $Q_2$ (không bao gồm $Q_2$ nếu n lẻ)

$Q_3$ là trung vị của nửa số liệu đã sắp xếp bên phải $Q_2$ (không bao gồm $Q_2$ nếu n lẻ)

+) Độ lệch chuẩn $S=\sqrt{S^2}$

Tính phương sai $S^2=\frac{1}{n}\left({x_1}^2+{x_2}^2+...+{x_n}^2\right)-{\overline{x}}^2$

b)

+) x là giá trị ngoại lệ nếu $x>Q_3+1,5.{\mathrm{\Delta }}_Q$ hoặc $x<Q_1-1,5.{\mathrm{\Delta }}_Q$

+) So sánh trung vị (do một mẫu có số liệu quá lớn so với các số liệu khác): nhà máy nào có trung vị lớn hơn thì có mức lương cao hơn.

Lời giải 

a) Nhà máy A:

+) Số trung bình: $\overline{x}=\frac{4+5+5+47+5+6+4+4}{8}=10$

+) Mốt: $M_o=4,M_o=5$

+) Tứ phân vị: $Q_1,Q_2,Q_3$

Sắp xếp mẫu số liệu theo thứ tự không giảm: 4; 4; 4; 5; 5; 5; 6; 47.

$Q_2=M_e=5$

$Q_1$ là trung vị của nửa số liệu: 4; 4; 4; 5. Do đó $Q_1=4$

$Q_3$ là trung vị của nửa số liệu: 5; 5; 6; 47. Do đó $Q_3=5,5$

+) Phương sai $S^2=\frac{1}{8}\left(4^2+5^2+...+4^2\right)-{10}^2=196$ => Độ lệch chuẩn $S=\sqrt{S^2}=14$

Nhà máy B:

+) Số trung bình: $\overline{x}=\frac{2+9+9+8+10+9+9+11+9}{9}=8,4$

+) Mốt: $M_o=9$

+) Tứ phân vị: $Q_1,Q_2,Q_3$

Sắp xếp mẫu số liệu theo thứ tự không giảm: 2; 8; 9; 9; 9; 9; 9; 10; 11

$Q_2=M_e=9$

$Q_1$ là trung vị của nửa số liệu: 2; 8; 9; 9. Do đó $Q_1=8,5$

$Q_3$ là trung vị của nửa số liệu: 9; 9; 10; 11. Do đó $Q_3=9,5$

+) Phương sai $S^2=\frac{1}{9}\left(2^2+9^2+...+9^2\right)-8,4^2=6,55$ => Độ lệch chuẩn $S=\sqrt{S^2}=2,56$

b)

Nhà máy A có: ${\mathrm{\Delta }}_Q=1,5$

Vậy giá trị ngoại lệ $x>5,5+1,5.1,5=7,75$ hoặc $x<4-1,5.1,5=1,75$ là 47.

Nhà máy B có: ${\mathrm{\Delta }}_Q=1$

Vậy giá trị ngoại lệ $x>9,5+1,5.1=11$ hoặc $x<8,5-1,5.1=7$ là 2.

Ta so sánh trung vị: $9>5$, do dó công nhân nhà máy B có mức lương cao hơn.

Chú ý

Ta không so sánh số trung bình vì có giá trị 47 quá lớn so với các giá trị còn lại.

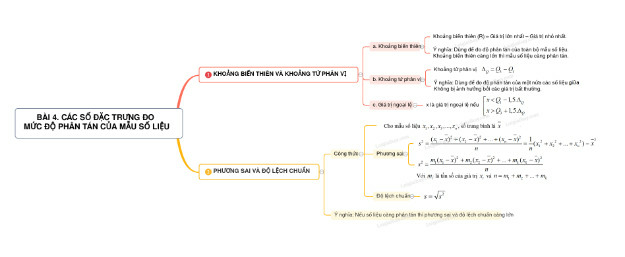
Lý thuyết Bài 4. Các số đặc trưng đo mức độ phân tán của mẫu số liệu

1. KHOẢNG BIẾN THIÊN VÀ KHOẢNG TỨ PHÂN VỊ

a. Khoảng biến thiên

Khoảng biến thiên (R) = Giá trị lớn nhất – Giá trị nhỏ nhất.

Ý nghĩa: Dùng để đo độ phân tán của toàn bộ mẫu số liệu: Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.

b. Khoảng tứ phân vị

Khoảng tứ phân vị:  ${\mathrm{\Delta }}_Q=Q_3-Q_1$

Ý nghĩa: Dùng để đo độ phân tán của một nửa các số liệu có giá trị thuộc đoạn từ $Q_1$ đến $Q_3$ trong mẫu.

Không bị ảnh hưởng bởi các giá trị bất thường.

c. Giá trị ngoại lệ

$x$ là giá trị ngoại lệ nếu $[\begin{array}{l}x<Q_1-1,5.{\mathrm{\Delta }}_Q\\ x>Q_3+1,5.{\mathrm{\Delta }}_Q\end{array}$

2. PHƯƠNG SAI VÀ ĐỘ LỆCH CHUẨN

Cho mẫu số liệu $x_1,x_2,x_3,...,x_n$, số trung bình là $\overline{x}$

+ Phương sai: $s^2=\frac{{(x_1-\overline{x})}^2+{(x_2-\overline{x})}^2+...+{(x_n-\overline{x})}^2}{n}=\frac{1}{n}({x_1}^2+{x_2}^2+...+{x_n}^2)-{\overline{x}}^2$

+ Độ lệch chuẩn: $s=\sqrt{s^2}$

Ý nghĩa: Nếu số liệu càng phân tán thì phương sai và độ lệch chuẩn càng lớn

Chú ý: Phương sai của mẫu số liệu cho dạng bảng tần số:

$s^2=\frac{m_1{(x_1-\overline{x})}^2+m_2{(x_2-\overline{x})}^2+...+m_k{(x_k-\overline{x})}^2}{n}$

Với $m_i$ là tần số của giá trị $x_i$ và $n=m_1+m_2+...+m_k$