Toptailieu.vn xin giới thiệu 50 bài tập trắc nghiệm Ôn tập chương 4  (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 9 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

Ôn tập chương 4

Câu 1: Tìm phương trình đường thẳng (d) đi qua điểm I (0; 1) và cắt parabol (P): y = x² tại hai điểm phân biệt M và N sao cho 

A. y = 2x + 1; y = −2x – 1                 

B. y = 2x + 1; y = −2x + 1

C. y = 2x + 1; y = 2x – 1                    

D. y = −2x + 2; y = −2x + 1

Lời giải:

Đường thẳng (d) qua I với hệ số góc a có dạng: y = ax + 1

Phương trình hoành độ giao điểm của (d) và (P) là x² = ax + 1 ⇔ x² − ax – 1 = 0 (1)

Vì ∆ = a² + 4 > 0 với mọi a, (1) luôn có hai nghiệm phân biệt nên (d) luôn cắt (P) tại hai điểm phân biệt M (x₁; y₁), N (x₂; y₂) hay M (x₁; ax₁ + 1), N (x₂; ax₂ + 1)

Vậy phương trình đường thẳng cần tìm là y = 2x + 1; y = −2x + 1

Đáp án cần chọn là: B

Câu 2: Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình 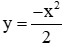. Gọi (d) là đường thẳng đi qua I (0; −2) và có hệ số góc k. Đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B. Gọi H, K theo thứ tự là hình chiếu vuông góc của A, B trên trục hoành. Khi đó tam giác IHK là tam giác?

A. Vuông tại H                        

B. Vuông tại K

C. Vuông tại I                          

D. Đều

Lời giải:

Đường thẳng (d): y = kx – 2

Xét phương trình 

Ta có: ∆ = k² + 4 > 0 với mọi k; suy ra (1) có hai nghiệm phân biệt

Vậy (d) luôn cắt (P) tại hai điểm phân biệt.

Giả sử (1) có hai nghiệm phân biệt x₁; x₂

Suy ra A (x₁; y₁), B (x₂; y₂) thì H (x₁; 0), K (x₂; 0)

Khi đó IH² = x₁² + 4, IK² = x₂² + 4, HK² = (x₁ – x₂)²

Theo định lý Vi-ét thì x₁x₂ = −4 nên IH² + IK² = x₁² + x₂² + 8 = KH²

Vậy tam giác IHK vuông tại I

Đáp án cần chọn là: C

Câu 3: Cho Parabol (P): y = x² và đường thẳng (d): y = mx + 4. Biết đường thẳng (d) luôn cắt đồ thị (P) tại hai điểm phân biệt A, B. Gọi x₁; x₂ là hoành độ của các điểm A, B. Tìm giá trị lớn nhất của 

Lời giải:

Phương trình hoành độ giao điểm của (d) và (P) là: x² = mx + 4 ⇔ x² − mx − 4 = 0. Ta có ∆ = m² + 16 > 0, với mọi m nên phương trình luôn có 2 nghiệm phân biệt, suy ra đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt.

Dấu “=” xảy ra khi m² + 8 = 2m + 7 ⇔ (m – 1)² = 0 ⇔ m = 1

Suy ra giá trị lớn nhất của Q là 1 khi m = 1

Đáp án cần chọn là: C

Câu 4: Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): 2x – y – a² = 0 và parabol (P): y = ax² (a > 0). Tìm a để (d) cắt (P) tại hai điểm phân biệt A, B. Khi đó có kết luận gì về vị trí của hai điểm A, B

A. Với 0 < a < 1 thì (d) cắt (P) tại hai điểm phân biệt A, B và A, B nằm ở bên phải trục Oy

B. Với  a > 0 thì (d) cắt (P) tại hai điểm phân biệt A, B và A, B nằm ở bên phải trục Oy

C. Với 0 < a < 1 thì (d) cắt (P) tại hai điểm phân biệt A, B và A, B nằm ở bên trái trục Oy

D. Với 0 < a < 1 thì (d) cắt (P) tại hai điểm phân biệt A, B và A, B nằm ở hai phía với trục Oy

Lời giải:

Ta có (d): 2x – y – a² = 0 ⇔ y = 2x − a²

Xét phương trình ax² = 2x – a²  ax² – 2x + a² = 0 (1) ⇔  ∆' > 0 ⇔ a < 1

Kết hợp với điều kiện a > 0 ta có 0 < a < 1 khi đó (1) có hai nghiệm x_A; x_B (x_A; x_B là  hoành độ của A và B) thỏa mãn 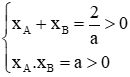 (hệ thức Vi-ét) suy ra x_A; x_B dương nên A, B nằm ở bên phải trục Oy.

Đáp án cần chọn là: A

Câu 5: Cho parabol (P): y = x² và đường thẳng (d): y = mx + 1. Gọi A (x₁; y₁) và B (x₂; y₂) là các giao điểm của (d) và (P). Tìm m để biểu thức M = (y₁ − 1)( y₂ − 1) đạt giá trị lớn nhất.

A. m = 0     

B. m = 2     

C. m = 1     

D. m = −1

Lời giải:

Phương trình hoành độ giao điểm của đường thẳng và Parabol là:

x² = mx + 1 ⇔ x² – mx – 1 = 0 (1)

∆ = m² + 4 > 0 với mọi m nên 91) có hai nghiệm phân biệt, suy ra (d) luôn cắt (P) tại hai điểm phân biệt A (x₁; y₁) và B (x₂; y₂) với x₁; x₂ là hai nghiệm của phương trình (1).

Theo định lý Vi-ét, ta có: x₁ + x₂ = m; x₁.x₂ = −1

Vì A; B  ∈(P) ⇒ y₁ = x₁²; y₂ = x₂²

Ta có

M = (y₁ − 1)(y₂ − 1) = (x₁²− 1) (x₂²  − 1) = x₁². x₂² – (x₁² + x₂²) + 1

= x₁². x₂²  + x₁². x₂²  − (x₁ + x₂)² + 1 = 1 – 2 − m² + 1 = −m² ≤ 0

Vậy MaxM = 0 khi m = 0

Đáp án cần chọn là: A

Câu 6: Trong mặt phẳng tọa độ Oxy cho Parabol (P): y = x² và đường thẳng (d): 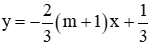 (m là tham số). Trong trường hợp (P) và (d) cắt nhau tại hai điểm phân biệt có hoành độ giao điểm là x₁; x₂. Đặt f (x) = x³ + (m + 1)x² – x khi đó?

Lời giải:

Xét phương trình hoành độ giao điểm của (d) và (P) ta có:

Ta thấy phương trình (1) có hệ số a và c trái dấu nên luôn có hai nghiệm phân biệt mọi m nên (P) và (d) luôn cắt nhau tại hai điểm phân biệt với mọi m

Vì f(x) = x³ + (m + 1)x² – x nên ta có:

f(x_1­) −  f(x_2­) = x₁³ – x₂³ + (m + 1)(x₁² – x₂²) − x₁ + x₂

⇒ 2(f(x_1­) −  f(x_2­)) = 2x₁³ – 2x₂³ − 3(x₁ + x₂)(x₁² – x₂²) − 2x₁ + 2x₂

= −x₁³ + x₂³ + 3x₁.x₂ (x₂ – x₁) – 2(x₁ − x₂) = −x₁³ + x₂³ + (x₁ − x₂) – 2(x₁ − x₂)

= −(x₁³ − x₂³ − 3x₁.x₂ (x₁ – x₂)) = [(x₁ − x₂)( x₁² + x₂² − 2 x₁.x₂)] = (x₁ − x₂)³

Đáp án cần chọn là: D

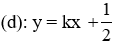
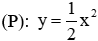
Câu 7: Trong mặt phẳng Oxy cho đường thẳng   và parabol . Giả sử đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B. Tọa độ trung điểm M của đoạn thẳng AB luôn thỏa mãn phương trình nào dưới đây?

Lời giải:

Xét phương trình hoành độ giao điểm của (d) và (P): 

⇔ x² – 2hx – 1 = 0 (*). Nhận thấy a = 1; c = −1 trái dấu nhau nên phương trình (*) luôn có hai nghiệm phân biệt hay đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A và B với mọi k

Gọi A(x_A; y_A); B(x_B; y_B) thì x_A; x_B là hai nghiệm của phương trình (*) và 

Đáp án cần chọn là: A

Câu 8: Trên parabol (P): y = x² ta lấy ba điểm phân biệt A (a; a²); B (b; b²); C (c; c²) thỏa mãn a² – b = b² – c = c² – a. Hãy tính tích T = (a + b + 1)(b + c + 1)(c + a + 1)

A. T = 2     

B. T = 1      

C. T = −1   

D. T = 0

Lời giải:

Đáp án cần chọn là: C

Câu 9: Cho parabol 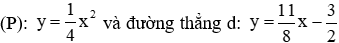. Gọi A, B là các giao điểm của (P) và d. Tìm tọa độ điểm C trên trục tung cho CA + CB có giá trị nhỏ nhất.

Lời giải:

Hoành độ của A và B là nghiệm của phương trình 

Dễ thấy hai điểm A, B cùng nằm về một phía so với trục tung (do cùng có hoành độ dương).

Lấy điểm A’ (− 4; 4) đối xứng với A qua trục tung

Khi đó CA + CB = CA’ + CB ≥ A’B, nên CA + CB đạt giá trị nhỏ nhất khi và chỉ khi A’, C, B thẳng hàng, tức là khi C là giao điểm của đường thẳng A’B với trục tung.

Phương trình đường thẳng d’ đi qua A’ và B có dạng y = ax + b

Suy ra giao điểm (d’) với trục tung có hoành độ 

Đáp án cần chọn là: B

Câu 10: Trong mặt phẳng Oxy, cho parabol (P): 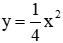 và đường thẳng (d): x – 2y + 12 = 0. Gọi giao điểm của (d) và (P) là A, B. Tìm tọa độ điểm C nằm trên (P) sao cho tam giác ABC vuông tại C.

A. C(2; 1)  

B. C(1; 2)  

C. C(1; 0)      

D. C(0; 2)

Lời giải:

Vậy 2 giao điểm A (6; 9), B (−4; 4)

Gọi 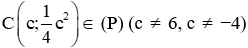 là điểm cần tìm.

Tam giác ABC vuông tại C khi và chỉ khi AB² = AC² + BC²

Vậy C (2; 1) là điểm thỏa mãn đề bài

Đáp án cần chọn là: A

Câu 11: Trên quãng đường AB, dài 210 km, tại cùng một thời điểm một xe máy khởi hành từ A đến B và một ô tô khởi hành từ B đến A. Sau khi gặp nhau, xe máy đi tiếp 4 giờ nữa thì đến B và ô tô đi tiếp 2 giờ 15 phút nữa thì đến A. Biết rằng vận tốc ô tô và xe máy không thay đổi trong suốt chặng đường. Vận tốc của xe máy và ô tô lần lượt là:

A. 20 km/h; 30 km/h                         

B. 30 km/h; 40 km/h

C. 40 km/h; 30 km/h                         

D. 45 km/h; 35 km/h

Lời giải:

Gọi vận tốc xe máy là x (km/h). Điều kiện: x > 0

Gọi vận tốc ô tô là y (km/h). Điều kiện: y > 0

Quãng đường xe máy đi được kể từ khi gặp ô tô cho đến khi đến B là: 4x (km)

Quãng đường ô tô đi được kể từ khi gặp xe máy cho đến khi đến A là: 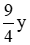 (km)

Vậy vận tốc xe máy là 30 km/h. Vận tốc ô tô là 40 km/h

Đáp án cần chọn là: B

Câu 12: Hai máy cày cùng làm việc trong 12 giờ thì cày được 1/10 khu đất. Nếu máy cày thứ nhất làm một mình trong 42 giờ rồi nghỉ và sau đó máy cày thứ hai làm một mình trong 22 giờ thì cả hai máy cày được 25% khu đất. Hỏi nếu làm một mình thì máy 2 cày trong bao lâu?

A. 250 giờ  

B. 300 giờ  

C. 150 giờ  

D. 200 giờ

Lời giải:

Gọi x (giờ) là thời gian máy cày 1 làm một mình xong khu đất.

Gọi y (giờ) là thời gian máy cày 2 làm một mình xong khu đất.

Điều kiện: x, y > 12

Mỗi giờ máy 1 và máy 2 làm được tương ứng là 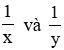 khu đất

Do 2 máy cùng cày trong 12 giờ được 1/10 khu đất nên ta có phương trình: 

Nếu máy 1 làm một mình 42 giờ và máy 2 làm một mình 22 giờ thì làm được 25% = 1/4 khu đất nên ta có phương trình 

Suy ra 

Vậy máy 1 làm một mình trong 300 giờ thì xong khu đất.

Máy 2 làm một mình trong 200 giờ thì xong khu đất.

Đáp án cần chọn là: D

Câu 13: Một ca nô chạy trên sông trong 8h xuôi dòng được 81km và ngược dòng 105km. Một lần khác, ca nô chạy trên sông trong 4h xuôi dòng được 54km và ngược dòng 42km. Tính vận tốc riêng của ca nô.

A. 23 km/h 

B. 25 km/h 

C. 26 km/h 

D. 24 km/h

Lời giải:

Gọi vận tốc riêng của ca nô và vận tốc dòng nước lần lượt là x, y (km/h; x > y > 0)

Suy ra vận tốc xuôi dòng của ca nô là x + y(km/h); vận tốc ngược dòng là x – y (km/h)

Ca nô chạy trên sông trong 8h xuôi dòng được 81 km và ngược dòng 105 km nên ta có phương trình: 

Ca nô chạy trên sông trong 4h xuôi dòng được 54km và ngược dòng 42km nên ta có phương trình: 

Vậy vận tốc riêng của ca nô và vận tốc dòng nước lần lượt là 24 km/h và 3 km/h

Đáp án cần chọn là: D

Câu 14: Hai ô tô khởi hành cùng 1 lúc từ A đến B cách nhau 300km. Ô tô thứ nhất mỗi giờ đi nhanh hơn ô tô thứ hai 10km nên đến B sớm hơn ô tô thứ hai 1h. Tìm vận tốc mỗi xe.

A. 60 km/h và 40 km/h                      

B. 30 km/h và 40 km/h

C. 60 km/h và 50 km/h                      

D. 50 km/h và 40 km/h

Lời giải:

Gọi vận tốc ô tô thứ nhất và thứ hai lần lượt là x và y (km/h; x, y > 0)

Ô tô thứ nhất mỗi giờ đi nhanh hơn ô tô thứ hai 10km nên ta có phương trình: x – y = 10 (1)

Ô tô thứ nhất đến sớm hơn ô tô thứ hai 1h nên ta có: 

Vậy vận tốc của ô tô thứ nhất và ô tô thứ hai lần lượt là 60 km/h và 50 km/h.

Đáp án cần chọn là: C

Câu 15: Theo kế hoạch, phân xưởng A phải sản xuất hơn phân xưởng B là 200 sản phẩm. Khi thực hiện, phân xưởng A tăng năng suất 20%, phân xưởng B tăng năng suất 15% nên phân xưởng A sản xuất hơn phân xưởng B là 350 sản phẩm. Hỏi theo kế hoạch mỗi phân xưởng A và B phải sản xuất số sản phẩm lần lượt là:

A. 2300 và 2500                               

B. 2500 và 1500

C. 2200 và 2400                               

D. 2400 và 2200

Lời giải:

Gọi x, y lần lượt là số sản phẩm phân xưởng A và B phải làm theo kế hoạch (sản phẩm) (x, y ∈ N*; x > 200)

Theo kế hoạch, phân xưởng A phải sản xuất nhiều hơn phân xưởng B là 200 sản phẩm nên ta có phương trình: x – y = 200               (1)

Thực tế, phân xưởng A vượt mức kế hoạch 20%, đội B vượt kế hoạch 15%, nên phân xưởng A sản xuất hơn phân xưởng B là 350 sản phẩm suy ra ta có:

x + 20%x – (y + 15%y) = 350 ⇔ 1,2x – 1,15y = 350                (2)

Từ (1) và (2) ta có hệ phương trình:

Vậy theo kế hoạch, phân xưởng A phải sản xuất 2400 sản phẩm, phân xưởng B phải sản xuất 2200 sản phẩm

Đáp án cần chọn là: D

Câu 16: Người ta thêm 1 kg nước vào dung dịch A thì được dung dịch B có nồng độ axit là 20%. Sau đó lại cho thêm 1 kg axit vào dung dịch B thì được dung dịch C có nồng độ axit là 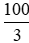%. Tính nồng độ axit trong dung dịch A.

A. 30%      

B. 40%       

C. 25%       

D. 20%

Lời giải:

Gọi khối lượng axit trong dung dịch A là x; khối lượng nước trong dung dịch A là y (kg; x, y > 0)

Người ta cho thêm 1kg nước vào dung dịch A thì được dung dịch B có nồng độ axit là 20% nên ta có:

Lại cho thêm 1kg axit vào dung dịch B thì được dung dịch C có nồng độ axit là 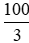% nên ta có:

Đáp án cần chọn là: C

Câu 17: Hai người thợ cùng làm 1 công việc. Nếu làm riêng, mỗi người nửa việc thì tổng thời gian 2 người làm là 12,5 giờ. Nếu 2 người cùng làm thì chỉ trong 6 giờ là xong việc. Hỏi nếu làm riêng cả công việc thì mỗi người làm mất bao lâu?

A. 7,5 giờ và 5 giờ                   

B. 10 giờ và 8 giờ

C. 8 giờ và 12 giờ                    

D. 15 giờ và 10 giờ

Lời giải:

Gọi thời gian người thứ nhất làm riêng để xong nửa công việc là x; thời gian người thứ hai làm riêng để xong nửa công việc là y (giờ; x, y > 0)

Nếu làm riêng, mỗi người nửa việc thì tổng thời gian 2 người làm là 12,5 giờ nên ta có phương trình: x + y = 12,5 (1)

Thời gian người thứ nhất làm riêng để xong cả công việc là 2x, của người thứ 2 là 2y. Mà 2 người cùng làm thì trong 6 giờ xong việc nên ta có phương trình: 

Từ (1) và (2) ta có hệ phương trình:

Vậy nếu làm riêng thì một người làm trong 2.7,5 = 15 giờ, còn người kia làm trong 2.5 = 10 giờ

Đáp án cần chọn là: D

Câu 18: Cho 3 vòi nước cùng chảy vào 1 bể. Biết vòi 1 và vòi 2 chảy đầy bể trong 72 phút. Vòi 1 và vòi 3 chảy đầy bể trong 63 phút. Vòi 2 và vòi 3 chảy đầy bể trong 56 phút. Hỏi vòi 2 và vòi 1 chảy một mình đầy bể trong bao lâu?

A. 168 phút

B. 120 phút

C. 126 phút

D. 110 phút

Lời giải:

Gọi thời gian vòi 1 chảy một mình đầy bể là x (phút), thời gian vòi 2 chảy mình đầy bể là y (phút), thời gian vòi 3 chảy mình đầy bể là z (phút), (x, y, z > 0)

Vậy thời gian vòi 1 chảy một mình đầy bể là 168 (phút), thời gian vòi 2 chảy mình đầy bể là 126 (phút), thời gian vòi 3 chảy mình đầy bể là 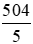 (phút).

Đáp án cần chọn là: C

Câu 19: Một hội trường có 150 ghế được sắp xếp ngồi theo các dãy ghế. Nếu có thêm 71 ghế thì phải kê thêm 2 dãy ghế, mỗi dãy phải thêm 3 ghế nữa. Tính số ghế mỗi dãy lúc đầu trong hội trường.

A. 14 ghế    

B. 18 ghế    

C. 20 ghế    

D. 10 ghế

Lời giải:

Gọi số dãy ghế trong hội trường là x (x nguyên dương)

Vì lúc sau mỗi dãy ghế lúc sau phải thêm 3 ghế nên ta có phương trình:

Vậy số ghế mỗi dãy là 10 ghế

Đáp án cần chọn là: D

Câu 20: Một hợp kim của đồng và kẽm nặng 124g có thể tích là 15cm³. Biết cứ 89g đồng thì có thể tích là 10cm³ và 7g kẽm thì có thể tích là 1cm³. Tính khối lượng đồng và kẽm trong hợp kim đó.

A. 32g và 96g                                   

B. 30g và 94g       

C. 80g và 44g                                   

D. 89g và 35g

Lời giải:

Gọi khối lượng đồng trong hợp kim là x (0 < x < 124)

Ta có khối lượng kẽm trong hợp kim là 124 – x

Vì 89g đồng thì có thể tích là 10cm³ nên x (g) đồng có thể tích là 

7g kẽm thì có thể tích là 1cm³ nên 124 – x (g) kẽm có thể tích là 

Vì thể tích của hợp kim ban đầu là 15cm³ nên ta có phương trình:

Vậy khối lượng đồng và kẽm trong hợp kim lần lượt là 89g và 35g

Đáp án cần chọn là: D

Câu 21: Chiều cao của một tam giác vuông là 8cm chia cạnh huyền thành 2 đoạn thẳng hơn kém nhau 12cm. Tính độ dài cạnh huyền của tam giác vuông đó.

A. 14cm     

B. 18cm     

C. 16cm     

D. 20cm

Lời giải:

Giả sử tam giác vuông ABC có đường cao AH chia cạnh BC thành 2 đoạn thẳng BH và CH

Gọi độ dài cạnh BH là x (cm) (x > 0)

Khi đó độ dài cạnh CH là x + 12 (cm)

Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:

Suy ra BH = 4cm và CH = 16cm

Vậy cạnh huyền BC = 20cm

Đáp án cần chọn là: D

Câu 22: Một tấm sắt hình chữ nhật có chu vi 96cm. Người ta cắt ở mỗi góc tấm sắt một hình vuông cạnh là 4cm. Diện tích còn lại của tấm sắt là 448cm². Tính các kích thước của tấm sắt biết chiều dài của tấm sắt có độ dài lớn hơn 20cm

A. 32cm và 16cm                                       

B. 30cm và 18cm

C. 28cm và 20cm                                        

D. 26cm và 22cm

Lời giải:

Nửa chu vi tấm sắt là 96 : 2 = 48 (cm)

Gọi chiều dài của tấm sắt là x (cm) (x > 20)

Chiều rộng của tấm sắt sẽ là 48 – x (cm)

Diện tích của tấm sắt ban đầu là x (48 – x) (cm²)

Người ta cắt ở mỗi góc tấm sắt một hình vuông cạnh là 4cm nên diện tích phần cắt đi là: 4.4.4 = 64 (cm²)

Diện tích còn lại của tấm sắt là 448cm² nên ta có phương trình:

Vậy chiều dài và chiều rộng của tấm sắt lần lượt là 32cm và 16cm

Đáp án cần chọn là: A

Câu 23: Một phân xưởng đặt kế hoạch sản xuất 200 sản phẩm. Trong 5 ngày đầu do còn làm việc khác nên mỗi ngày phân xưởng sản xuất ít hơn mức đề ra là 4 sản phẩm. Trong những ngày còn lại, xưởng sản xuất vượt mức 10 sản phẩm mỗi ngày nên hoàn thành kế hoạch sớm hơn 1 ngày. Hỏi theo kế hoạch, mỗi ngày phân xưởng cần sản xuất bao nhiêu sản phẩm?

A. 30 sản phẩm                       

B. 25 sản phẩm

C. 22 sản phẩm                       

D. 20 sản phẩm

Lời giải:

Gọi năng suất làm việc theo dự kiến của xí nghiệp là x(sản phẩm/ngày), (x > 4)

+) Theo dự kiến: Mỗi ngày phân xưởng sản xuất x sản phẩm, tổng sản phẩm là 200 sản phẩm và thời gian sản xuất là 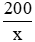 ngày

+ Thực tế: 5 ngày đầu phân xưởng sản xuất x – 4 (sản phẩm/ngày), số sản phẩm sản xuất được là 5 (x – 4). Những ngày sau mỗi ngày phân xưởng sản xuất x + 10 (sản phẩm/ngày), số sản phẩm sản xuất được là 220 – 5x với thời gian sản xuất là 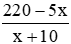 (ngày)

*) Vì thực tế xí nghiệp đã hoàn thành công việc sớm hơn 1 ngày so với dự định nên ta có phương trình:  

Vậy theo dự kiến mỗi ngày phân xưởng sản xuất 20 sản phẩm

Đáp án cần chọn là: D

Câu 24: Một công nhân được giao làm một số sản phẩm trong thời gian nhất định. Khi còn làm nốt 30 sản phẩm cuối cùng người đó thấy nếu cứ giữ nguyên năng suất thì sẽ chậm 30 phút. Nếu tăng năng suất thêm 55 sản phẩm một giờ thì sẽ xong sớm hơn dự định là 30 phút. Tính năng suất của người thợ lúc đầu.

A. 2520      

B. 20          

C. 15          

D. 10

Lời giải:

Gọi x (sản phẩm) là năng suất lúc đầu của công nhân đó (x > 0)

+) Nếu năng suất là x sản phẩm thì thời gian làm là 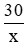 h

+) Nếu năng suất là x + 5 sản phẩm thì thời gian làm là 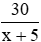 h

Vì thời gian chênh lệch nếu vẫn giữ nguyên năng suất và tăng tăng suất là 1 giờ nên ta có phương trình:

Vậy năng suất lúc đầu của người công nhân đó là 10 sản phẩm

Đáp án cần chọn là: D

Câu 25: Một người dự định đi xe đạp từ A đến B cách nhau 36km trong thời gian đã định. Sau khi đi được nửa quãng đường, người đó dừng lại nghỉ 30 phút. Vì vậy mặc dù trên quãng đường còn lại đã tăng tốc thêm 2km/h song vẫn đến B chậm hơn dự kiến 12 phút. Vậy vận tốc của người đi xe đạp trên đoạn đường cuối của đoạn AB?

A. 12 km/h 

B. 14 km/h 

C. 10 km/h 

D. 8 km/h

Lời giải:

Gọi vận tốc dự định đi của người đó là x (km/h) (x > 0)

Thời gian dự định đi của người đó là 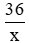 (h)

Thời gian người đó đi nửa quãng đường đầu là 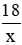 (h)

Nửa quãng đường sau người đó đi với vận tốc là x + 2 (km/h) và thời gian người đó đi là 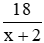 (h)

Vì nghỉ lại 30 phút nên thời gian đi từ lúc xuất phát đến khi tới B là 

Do người đó đến B chậm hơn dự kiến 12 phút 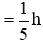 nên ta có phương trình:

Vậy vận tốc của người đi xe đạp trên đoạn đường cuối của đoạn AB là 12 km/h

Đáp án cần chọn là: A

Câu 26: Một ô tô đi từ tỉnh A đến tỉnh B cách nhau 120km. Cùng lúc đó có một xe máy chạy từ B trở về A và gặp xe ô tô C cách một trong hai điểm khởi hành 75km. Tính vận tốc của mỗi xe, biết rằng nếu vận tốc của hai xe không đổi và xe máy khởi hành trước ô tô 48 phút thì sẽ gặp nhau ở giữa quãng đường.

A. 30 km/h và 40 km/h                      

B. 50 km/h và 30 km/h

C. 50 km/h và 40 km/h                      

D. 30 km/h và 50 km/h

Lời giải:

Gọi vận tốc của ô tô là x (km/h) (x > 0)

Vì hai xe cùng xuất phát nên khi hai xe gặp nhau thì thời gian đi của hai xe là bằng nhau và khi đó ô tô đi được 75 km còn xe máy đi được 45 km

Thời gian ô tô và xe máy đi cho đến khi gặp nhau là 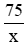 (h)

Vận tốc của xe máy là: 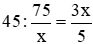 (km/h)

Nếu xe máy đi trước ô tô 48 phút 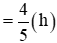 thì quãng đường đi được của 2 xe bằng nhau và bằng 60km

Thời gian đi quãng đường 60km của ô tô là: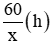  

Thời gian đi quãng đường 60km của xe máy là: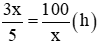  

Theo bài ra ta có phương trình: 

Vậy vận tốc của ô tô là 50 km/h, vận tốc của xe máy là 30 km/h

Đáp án cần chọn là: B

Câu 27: Phân tích đa thức f(x) = x⁴ – 2mx² – x + m² – m thành tích của hai tam thức bậc hai ẩn x.

A. f(x) = (m + x² – x – 1)(m + x² + x)

B. f(x) = (m − x² – x – 2)(m − x² + x)

C. f(x) = (m − x² – x – 1)(m − x² + x + 1)

D. f(x) = (m − x² – x – 1)(m − x² + x)

Lời giải:

Ta có: x⁴ – 2mx² – x + m² – m = 0 ⇔  m² – (2x² + 1)m + x⁴ – x = 0

Ta coi đây là phương trình bậc hai ẩn m và có:

∆_m = (2x² + 1)² – 4(x⁴ – x) = 4x² + 4x + 1 = (2x + 1)² ≥ 0

Do đó f(x) = (m − x² – x – 1)(m − x² + x)

Đáp án cần chọn là: D

Câu 28: Cho phương trình x² – 4x = 2|x – 2| − m – 5, với m là tham số. Xác định m để phương trình có bốn nghiệm phân biệt

A. m < 1     

B. −1 < m < 0       

C. 0 < m < 1

D. m > 0

Lời giải:

Ta có: x² – 4x = 2|x – 2| − m – 5 ⇔ (x² – 4x + 4) – 2|x – 2| = −m – 1

⇔ (x – 2)² – 2|x – 2| = −m – 1 (1)

Đặt t = |x −2| ≥ 0. Khi đó (1) thành: t² – 2t + 1 + m = 0    (2)

Để (1) có 4 nghiệm phân biệt thì (2) có hai nghiệm phân biệt dương, tức là phải có:

 thỏa mãn yêu cầu bài toán

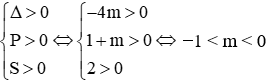
Đáp án cần chọn là: C

Câu 29: Tìm m để phương trình 3x² + 4(m – 1)x + m² – 4m + 1 = 0 có hai nghiệm phân biệt x₁; x₂ thỏa mãn: 

A. m = 1; m = 5    

B. m = 1; m = −1  

C. m = 5     

D. m ≠ 1

Lời giải:

Trước hết phương trình phải có hai nghiệm phân biệt x₁; x₂ khác 0 nên:

Thay vào (*) ta thấy m = −1 không thỏa mãn

Vậy m = 1; m = 5 là giá trị cần tìm

Đáp án cần chọn là: A

Câu 30: Tìm các giá trị của m để phương trình x² – mx + m² – m – 3 = 0 có hai nghiệm x₁; x₂ là độ dài các cạnh góc vuông của tam giác ABC tại A biết độ dài cạnh huyền BC = 2

Lời giải:

Vì độ dài cạnh của tam giác vuông là số dương nên x₁; x₂ > 0

Theo định lý Vi-ét ta có  

Điều kiện để phương trình có nghiệm là:

∆ = m² – 4(m² – m – 3) ≥ 0 ⇔ 3m²– 4m – 12 ≤ 0  (2)

Từ giả thiết suy ra x₁² + x₂² = 4 ⇔ (x₁ + x₂)² – 2x₁.x₂ = 4. Do đó

m² – 2(m² – m – 3) = 4 ⇔ m² – 2m – 2 = 0 ⇔ m = 1    

Thay m = 1 ± √3  vào (1) và (2) ta thấy chỉ có m = 1 + √3 thỏa mãn.

Vậy giá trị cần tìm là m = 1 + √3

Đáp án cần chọn là: C

Câu 31: Cho phương trình x⁴ – mx³ + (m + 1)x² – m(m + 1)x + (m + 1)² = 0

Lời giải:

Khi m = −2, ta có phương trình x⁴ + 2x³ − x² – 2x + 1 = 0

Kiểm tra ta thấy x = 0 không là nghiệm của phương trình

Chia hai vế của phương trình cho x²+ ta được:

Đặt 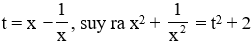. Thay vào phương trình nêu trên ta được:

t² + 2t – 1 = 0 ⇔ t = −1

Đáp án cần chọn là: A

Câu 32: Có bao nhiêu giá trị của m để phương trình x² – (2m + 1)x + m² + 1 = 0 (1) có hai nghiệm phân biệt x₁; x₂ thỏa mãn (x₁; x₂)² = x₁

A. 2            

B. 3            

C. 4            

D. 1

Lời giải:

Để phương trình đã cho có 2 nghiệm phân biệt thì

Vậy 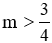 thì phương trình có hai nghiệm phân biệt

Với 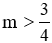 thì phương trình có hai nghiệm phân biệt x₁; x₂

Vậy 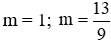 thỏa mãn điều kiện bài toán

Đáp án cần chọn là: A

Câu 33: Cho phương trình x² – (m – 1)x – m² + m – 2 = 0, với m là tham số. Gọi hai nghiệm của phương trình đã cho là x₁; x₂. Tìm m để biểu thức 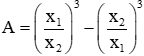 đạt giá trị lớn nhất

A. m = 4     

B. m = 3               

C. m = 2     

D. m = 1

Lời giải:

+) Xét 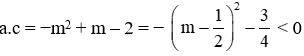 với mọi m ∈ R

Vậy phương trình luôn có hai nghiệm trái dấu với mọi m

+) Gọi hai nghiệm của phương trình đã cho là x₁; x₂

Vì phương trình luôn có hai nghiệm trái dấu nên x₁x₂ ≠ 0, do đó A được xác định với mọi x₁; x₂

Do x₁; x₂ trái dấu nên 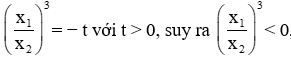, suy ra A < 0

Khi đó 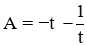 mang giá trị âm và A đạt giá trị lớn nhất khi –A có giá trị nhỏ nhất.

Ta có 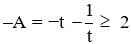 (BĐT Cô-si), suy ra A ≤ −2. Đẳng thức xảy ra khi và chỉ khi 

Vậy với m = 1 thì biểu thức A đạt giá trị lớn nhất là −2

Đáp án cần chọn là: D

Câu 34: Cho phương trình 2x² + 2mx + m² – 2 = 0, với m là tham số. Gọi x₁; x₂ là hai nghiệm của phương trình. Tìm hệ thức liên hệ giữa x₁; x₂ không phụ thuộc vào m.

A. x₁.x₂ = x₂ – x₁ + 1                         

B. x₁ − x₂  = x₂ – x₁ – 1

C. x₁.x₂ = x₂ – x₁ + 1                         

D. x₁.x₂ = x₁ + x₂ − 1

Lời giải:

Ta có ∆ = m² – 4(m – 1) = (m – 2)² ≥ 0, với mọi m

Do đó phương trình luôn có nghiệm với mọi giá trị của m

Theo hệ thức Vi-ét, ta có x₁ + x₂ = m và x₁.x₂ = m – 1

Thay m = x₁ + x₂ vào x₁.x₂ = m – 1, ta được x₁.x₂ = x₁ + x₂ – 1

Vậy hệ thức liên hệ giữa x₁; x₂ không phụ thuộc vào m là x₁.x₂ = x₁ + x₂ – 1

Đáp án cần chọn là: D

Câu 35: Cho phương trình x² – (2m + 1)x + 2m² – 3m + 1 = 0, với m là tham số. Gọi x₁; x₂ là nghiệm của phương trình. Chọn câu đúng.

Lời giải:

Ta có ∆' =(m – 1)² – (2m² – 3m + 1) = −m² + m = m(1 – m). Để phương trình có hai nghiệm 

Đáp án cần chọn là: A

Câu 36: Cho phương trình x² – (2m + 1)x + m² + 1 = 0, với m là tham số. Tìm tất cả các giá trị của m ∈ Z để phương trình có hai nghiệm phân biệt x₁; x₂ sao cho biểu thức 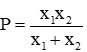 có giá trị là số nguyên

A. m = 1     

B. m = 2     

C. m = −2   

D. m = 0

Lời giải:

Ta có ∆ = (2m + 1)² – 4(m² + 1) = 4m – 3. Để phương trình có hai nghiệm phân biệt 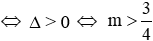. Theo định lý Vi-ét ta có:

x₁ + x₂ = 2m + 1 và x₁.x₂ = m² + 1.

Để P ∈ Z thì ta phải có (2m + 1) là ước của 5, suy ra 2m + 1 = 5 ⇔ m = 2

Thử lại với m = 2, ta được P = 1 (thỏa mãn)

Vậy m = 2 là giá trị cần tìm thỏa mãn bài toán.

Đáp án cần chọn là: B

Câu 37: Cho phương trình x² – 2(m + 1)x + m² + 2, với m là tham số. Khi phương trình có hai nghiệm x₁; x₂ thì biểu thức P = x₁ x₂ – 2(x₁ + x₂) – 6 có giá trị nhỏ nhất là:

A. −10       

B. 0            

C. −11        

D. −12

Lời giải:

Ta có ∆' = (m + 1)² – (m² + 2) = 2m – 1

Để phương trình có hai nghiệm 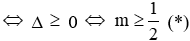. Theo định lý Vi-ét ta có:

x₁ + x₂ = 2m + 2 và x₁.x₂ = m² + 2. Ta có:

P = x₁.x₂ – 2(x₁ + x₂) – 6 = m² + 2 – 2(2m + 2) – 6 = m² – 4m – 8

= (m – 2)² – 12 ≥ −12

Dấu “=” xảy ra khi và chỉ khi m = 2 thỏa mãn điều kiện (*)

Vậy với m = 2 thì biểu thức P đạt giá trị nhỏ nhất −12

Đáp án cần chọn là: D

Câu 38: Gọi x₁; x₂ là hai nghiệm của phương trình 2x² – (3a – 1)x – 2 = 0. Tìm giá trị nhỏ nhất của biểu thức: 

A. 24          

B. 20          

C. 21          

D. 23

Lời giải:

Ta có ∆ =(3a – 1)² + 16 > 0 ⇒ Phương trình luôn có hai nghiệm phân biệt.

Vậy giá trị nhỏ nhất của P là 24

Đáp án cần chọn là: A

Câu 39: Giả sử phương trình bậc hai ax² + bx + c = 0 có hai nghiệm thuộc [0; 3]. Tìm giá trị lớn nhất của biểu thức: 

A. 5            

B. 4            

C. 2            

D. 3

Lời giải:

Vì phương trình bậc hai có 2 nghiệm nên a ≠ 0. Biểu thức Q có dạng đẳng cấp bậc hai ta chia cả tử và mẫu của Q cho a² thì  

Gọi x₁; x₂ là hai nghiệm của phương trình, theo Vi-ét ta có 

Ta đánh giá (x₁ + x₂)² qua x₁x₂ với điều kiện x₁; x₂ ∈ [0; 3]

Vậy giá trị lớn nhất của Q là 3

Đáp án cần chọn là: D

Câu 40: Cho phương trình x² – (m + 1)x – 3 = 0  (1), với x là ẩn, m là tham số. Gọi x₁; x₂ là hai nghiệm của phương trình (1). Đặt 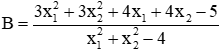. Tìm m khi B đạt giá trị lớn nhất.

Lời giải:

Phương trình x² – (m + 1)x – 3 = 0  (1)

+ Nhận xét ∆ = (m + 1)² + 12 > 0, ∀ m ∈ R. Suy ra (1) luôn có hai nghiệm phân biệt x₁; x₂

+ Nếu B ≠ 3 thì (*) là phương trình bậc 2 ẩn m. Phương trình (*) có nghiệm m khi và chỉ khi ∆' ≥ 0

Hay (B – 5)² – (B – 3)(3B – 20) ≥ 0 ⇔ 2B² – 19B + 35 ≤ 0

⇔ (2B – 5)(B – 7) ≤ 0 

Đáp án cần chọn là: A

Câu 41: Cho phương trình x² + 2(m – 3)x + m² + m + 1 = 0 (1). Khẳng định nào trong các khẳng định sau đúng:

A. Với m = 3 phương trình (1) có 2 nghiệm phân biệt

B. Với m = −1 phương trình (1) có nghiệm duy nhất

C. Với m = 2 phương trình (1) vô nghiệm

D. Với m = 2 phương trình (1) có 2 nghiệm phân biệt

Lời giải:

Phương trình (1) là phương trình bậc hai với ẩn x và tham số m

Xét: ∆' = (m – 3)² – (m² + m + 1) = m² – 6m + 9 − m² – m – 1 = −7m + 8

● Phương trình đã cho vô nghiệm ⇔ ∆' < 0 ⇔ −7m + 8 < 0 ⇔ m > 

● Phương trình đã cho có nghiệm duy nhất ∆' = 0 ⇔ −7m + 8 = 0 ⇔ m = 

● Phương trình đã cho có hai nghiệm phân biệt ∆' > 0 ⇔ −7m + 8 > 0 ⇔  m < 

Như vậy:

+ Với m = 3 > 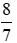 thì phương trình vô nghiệm nên A sai.

+ Với m = −1 < 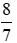 thì phương trình có hai nghiệm phân biệt nên B sai

+ Với m = 2 > 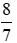 thì phương trình vô nghiệm nên C đúng, D sai.

Vậy đáp án đúng là đáp án C

Đáp án cần chọn là: C

Câu 42: Cho phương trình bậc hai: x² + ax + b = 0 (1) có hai nghiệm phân biệt x₁; x₂. Điều kiện để x₁; x₂ > 0 là:

Lời giải:

Để phương trình (1) có 2 nghiệm phân biệt x₁; x₂ nên ∆ > 0 ⇔ a² > 4b

Để phương trình (1) có 2 nghiệm dương phân biệt thì:

Đáp án cần chọn là: A

Câu 43: Giả sử x₁; x₂ là hai nghiệm của phương trình x² – 4x – 9 = 0. Khi đó x₁² + x₂²  bằng:

A. 30          

B. 32          

C. 34          

D. 36

Lời giải:

Phương trình đã cho có: ∆' = (−2)² – 1.(−9) = 13 > 0 nên có hai nghiệm phân biệt

Ta có x₁² + x₂² = x₁² + 2x₁x₂ + x₂² − 2x₁x₂ = (x₁ + x₂)² − 2x₁x₂  (1)

Áp dụng hệ thức Vi-ét ta có: 

Thay vào (1) ta được x₁² + x₂² =  4² – 2.(−9) = 16 + 18 = 34

Đáp án cần chọn là: C

Câu 44: Lập phương trình bậc hai có hai nghiệm là √5 − 2 và √5 + 2

A. x² − 2√5x + 1 = 0              

B. x² − 3√5x + 2 = 0

C. x² + 2√5x + 1 = 0              

D. x² − 3√5x − 2 = 0

Lời giải:

Ta có S = √5 − 2 + √5 + 2 = 2√5

P = (√5  − 2)(√5  + 2) = 5 – 4 = 1

Nhận thấy S² > 4P (do (2√5)² = 20 > 4)

Nên phương trình bậc hai có hai nghiệm là √5 − 2 và √5 + 2 là

x² − 2√5x + 1 = 0

Đáp án cần chọn là: A

Câu 45: Tập nghiệm của phương trình x⁴ − 5x² + 6 = 0 là:

Lời giải:

x⁴ − 5x² + 6 = 0 (1)

Đặt x² = t (t ≥ 0)

(1) ⇔ t² – 5t + 6 = 0

Có ∆ = 5² – 4.6 = 1 > 0 ⇒ Phương trình có hai nghiệm phân biệt

Đáp án cần chọn là: B

Câu 46: Tập nghiệm của phương trình x + 4√x − 12 = 0 là:

A. S = {36}

B. S = {4; 36}      

C. S = {4}  

D. S = {2; −6}

Lời giải:

x + 4√x − 12 = 0 (1)

ĐKXĐ: x ≥ 0

Đặt √x = t (t ≥ 0)

(1) ⇔ t² + 4t – 12 = 0.

Có ∆ = 2² + 12 = 16 > 0 ⇒ Phương trình có hai nghiệm phân biệt

Với t = 2 ⇒  √x = 2 ⇔ x = 4

Đáp án cần chọn là: C

Câu 47: Cho phương trình x⁴ + mx² + 2m + 3 = 0 (1). Với giá trị nào dưới đây của m thì phương trình (1) có 4 nghiệm phân biệt?

Lời giải:

Đặt x² = t (t ≥ 0) ta được: t² + mt + 2m + 3 = 0  (2)

Để phương trình (1) có 4 nghiệm phân biệt thì phương trình (2) có 2 nghiệm dương phân biệt

Phương trình (2) có hai nghiệm dương phân biệt 

Với các giá trị thuộc 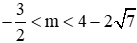 thì phương trình đã cho có 4 nghiệm phân biệt

Nhận thấy trong các đáp án thì chỉ có 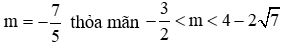 để phương trình đã cho có 4 nghiệm phân biệt

Đáp án cần chọn là: A

Câu 48: Cho phương trình bậc hai: x² – 2px + 5 = 0 có 1 nghiệm x₁ = 2. Tìm giá trị của p và nghiệm x₂ còn lại.

Lời giải:

Đáp án cần chọn là: C

Câu 49: Cho phương trình bậc hai: x² – qx + 50 = 0. Tìm q > 0 và 2 nghiệm x₁; x₂ của phương trình biết rằng x₁ = 2x₂

A. q = 5; x₁ = 10; x₂ = 5                     

B. q = 15; x₁ = 10; x₂ = 5

C. q = 5; x₁ = 5; x₂ = 10                     

D. q = −15; x₁ = −10; x₂ = −5

Lời giải:

Để phương trình đã cho có 2 nghiệm thì:

Khi đó phương trình có hai nghiệm x₁; x₂ thỏa mãn hệ thức Vi-ét 

Với x₁ = 2x₂ thì 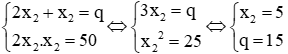 (do q > 0 nên x₂ = 5 > 0)

Khi đó: x₁ = 2x₂ = 2.5 = 10

Vậy q = 15; x₁ = 10; x₂ = 5

Đáp án cần chọn là: B

Câu 50: Cho phương trình: x² – (m + 2)x + (2m – 1) = 0 có hai nghiệm phân biệt x₁; x₂. Hệ thức liên hệ giữa 2 nghiệm không phụ thuộc vào giá trị của m là:

A. 2(x₁ + x₂) − x₁.x₂ = −5                  

B. x₁ + x₂ − x₁.x₂ = −1

C. x₁ + x₂ + 2x₁.x₂ = 5                       

D. 2(x₁ + x₂) − x₁.x₂ = 5

Lời giải:

Phương trình đã cho có 2 nghiệm phân biệt ⇔ ∆  > 0 ⇔ (m + 2)² – 4(2m – 1) > 0

⇔ m² + 4m + 4 – 8m + 4 > 0 ⇔ m² – 4m + 8 > 0 ⇔ (m – 2)² + 4 > 0 (∀m)

Vậy với mọi m phương trình đã cho luôn có 2 nghiệm phân biệt

Vậy 2(x₁ + x₂) − x₁.x₂ = 5 là hệ thức liên hệ giữa 2 nghiệm không phụ thuộc vào giá trị của m

Đáp án cần chọn là: D