Toptailieu.vn giới thiệu Giải bài tập Toán 9 Ôn tập chương 4 chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Căn bậc hai lớp 9.
Giải bài tập Toán 9 Ôn tập chương 4
Trả lời câu hỏi giữa bài:
Trả lời phần câu hỏi 1 trang 60 SGK toán 9 tập 2: Hãy vẽ đồ thị của các hàm số Dựa vào đồ thị để trả lời các câu hỏi sau:
a) Nếu a > 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào?
Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?
Nếu a < 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
b) Đồ thị của hàm số có những đặc điểm gì (trường hợp a > 0 , trường hợp a < 0)
Phương pháp giải:
Dựa vào tính chất và đặc điểm của đồ thị hàm số
Lời giải:
Vẽ đồ thị:
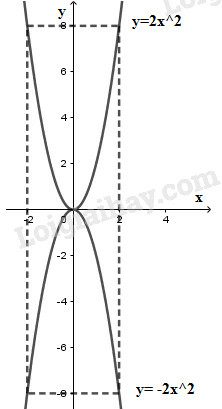
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị nào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.
Trả lời phần câu hỏi 2 trang 60 SGK toán 9 tập 2: Đối với phương trình bậc hai hãy viết công thức tính
Khi nào thì phương trình vô nghiệm?
Khi nào phương trình có hai nghiệm phân biệt? Viết công thức nghiệm.
Khi nào phương trình có nghiệm kép? Viết công thức nghiệm.
Vì sao khi a và c trái dấu thì phương trình có hai nghiệm phân biệt?
Phương pháp giải:
Dựa vào kiến thức về công thức nghiệm và công thức nghiệm thu gọn
Lời giải:
* Xét phương trình bậc hai một ẩn
và biệt thức , với
TH1. Nếu (hoặc thì phương trình vô nghiệm.
TH2. Nếu (hoặc thì phương trình có nghiệm kép: (hoặc )
TH3. Nếu (hoặc thì phương trình có hai nghiệm phân biệt: (hoặc )
* Khi a và c trái dấu thì nên , do đó phương trình có hai nghiệm phân biệt.
Trả lời phần câu hỏi 3 trang 60 SGK toán 9 tập 2: Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai
Nêu điều kiện để phương trình có một nghiệm bằng 1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
Nêu điều kiện để phương trình có một nghiệm bằng -1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
Phương pháp giải:
Áp dụng kiến thức về hệ thức Vi-et và ứng dụng.
Lời giải:
+ Hệ thức Vi-ét:
Nếu là hai nghiệm của phương trình thì:
+) Nếu phương trình có thì phương trình có một nghiệm , còn nghiệm kia là
Áp dụng: Phương trình có nên , do đó phương trình có một nghiệm , còn nghiệm kia là
+) Nếu phương trình có thì phương trình có nghiệm là , còn nghiệm kia là .
Áp dụng: Phương trình có nên , do đó phương trình có một nghiệm , còn nghiệm kia là
Trả lời phần câu hỏi 4 trang 60 SGK toán 9 tập 2: Nêu cách tìm hai số, biết tổng S và tích P của chúng.
Tìm hai số u và v trong mỗi trường hợp sau:
Phương pháp giải:
Tìm hai số khi biết tổng và tích của chúng
Nếu hai số có tổng bằng và tích bằng và thì hai số đó là hai nghiệm của phương trình: .
Lời giải:
+) Tìm hai số khi biết tổng và tích của chúng
Nếu hai số có tổng bằng và tích bằng và thì hai số đó là hai nghiệm của phương trình: .
a) Đặt ta có
Ta có:
Khi đó là hai nghiệm của phương trình
Ta có:
Nên phương trình có hai nghiệm phân biệt:
Vậy
Hoặc
b)
Đặt ta có
Ta có: nên không có hai số thỏa mãn đề bài.
Trả lời phần câu hỏi 5 trang 60 SGK toán 9 tập 2: Nêu cách giải phương trình trùng phương
Phương pháp giải:
Đặt ẩn phụ (1) (điều kiện
Từ đó đưa về phương trình bậc hai ẩn t đã biết cách giải.
Lời giải chi tiết:
Xét phương trình
Đặt ẩn phụ (1) (điều kiện
Khi đó phương trình đã cho tương đương với một phương trình bậc 2 ẩn t là:
(2)
- Giải phương trình (2) để tìm t, so sánh với điều kiện.
- Thay giá trị t thỏa mãn vào (1) để tìm x
Bài tập trang 63-64 SGK Toán 9
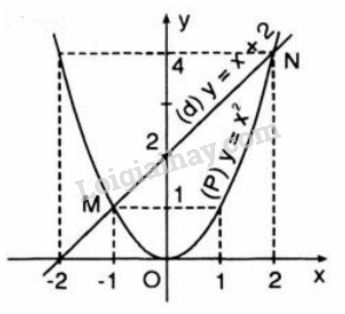
Bài 54 trang 63 SGK Toán 9 tập 2: Vẽ đồ thị của hàm số và trên cùng một hệ trục tọa độ
a) Qua điểm kẻ đường thẳng song song với trục Ox. Nó cắt đồ thị của hàm số tại hai điểm M và M’. Tìm hoành độ của M và M’.
b) Tìm trên đồ thị của hàm số điểm N có cùng hoành độ với M, điểm N’ có cùng hoành độ với M’. Đường thẳng NN’ có song song với Ox không? Vì sao? Tìm tung độ của N và N’ bằng hai cách:
- Ước lượng trên hình vẽ:
- Tính toán theo công thức.
Phương pháp giải:
Các bước vẽ đồ thị hàm số
- Bước 1: lập bảng giá trị x, y tương ứng (ít nhất 5 giá trị)
- Bước 2: Vẽ đồ thị hàm số: Nối các điểm trên hệ trục tọa độ, ta được đồ thị hàm số
+) Đồ thị hàm số với là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó được gọi là 1 parabol đỉnh O.
a) Giải phương trình hoành độ giao điểm để tìm hoành độ của M và M'
b) Điểm thuộc đồ thị hàm số thì
Lời giải:
Vẽ đồ thị hàm số:
* Hàm số và
- Tập xác định
- Bảng giá trị
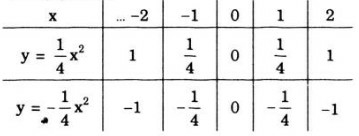
- Đồ thị hàm số và là các Parabol có đỉnh là gốc tọa độ O và nhận Oy làm trục đối xứng. Đồ thị hàm số nằm trên trục hoành, đồ thị hàm số nằm dưới trục hoành.
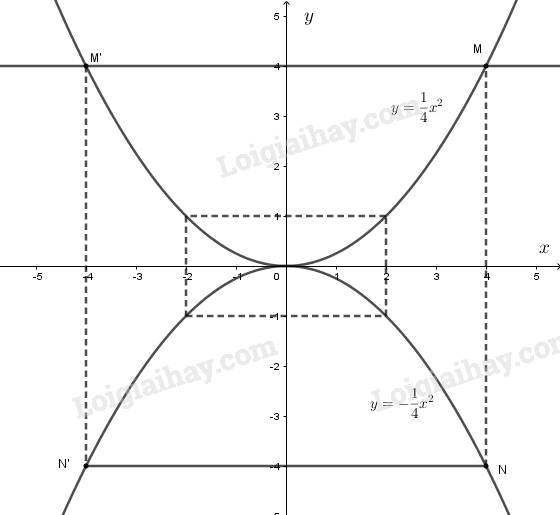
a) Đường thẳng qua song song với có dạng: y = 4.
Phương trình hoành độ giao điểm của đường thẳng y = 4 và đồ thị hàm số là:
Từ đó ta có hoành độ của là , của là .
b) Trên đồ thị hàm số ta xác định được điểm và có cùng hoành độ với . Ta được đường thẳng
Tìm tung độ của
- Ước lượng trên hình vẽ được tung độ của là ; của là
- Tính toán theo công thức:
Điểm . Thay vào nên
Điểm . Thay vào nên
Vậy tung độ của cùng bằng .
Bài 55 trang 63 SGK Toán 9 tập 2: Cho phương trình
a) Giải phương trình
b) Vẽ hai đồ thị và trên cùng một hệ trục tọa độ.
c) Chứng tỏ rằng hai nghiệm tìm được trong câu a) là hoành độ giao điểm của hai đồ thị.
Phương pháp giải:
a) Giải phương trình bằng cách sử dụng công thức nghiệm hoặc
+) Xét phương trình bậc hai:
Nếu phương trình có thì phương trình có một nghiệm là nghiệm kia là
b) Lập bảng giá trị rồi vẽ hai đồ thị hàm số c) Thay hai nghiệm tìm được ở câu a) vào mỗi hàm số để so sánh các giá trị của
Lời giải:
a) Giải phương trình:
b) Vẽ đồ thị hàm số
- Hàm số
+ Bảng giá trị:
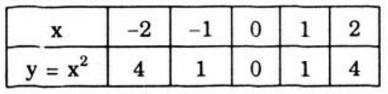
- Hàm số
+ Cho được điểm
+ Cho được điểm
Đồ thị hàm số:
c) Ta có phương trình hoành độ giao điểm của hai đồ thị là:
có nên có hai nghiệm
Điều này chứng tỏ rằng đường thẳng cắt đồ thị parapol tại hai điểm có hoành độ lần lượt là . Hai giá trị này cũng chính là nghiệm của phương trình ở câu a).
Bài 56 trang 63 SGK Toán 9 tập 2: Giải các phương trình:
a) ;b) ;c)
Phương pháp giải:
Phương pháp giải phương trình trùng phương: Đặt . Sau đó giải phương trình ẩn t theo công thức nghiệm của phương trình bậc 2. Tìm t đối chiếu điều kiện, từ đó thay vào cách đặt để tìm ra x.
Lời giải:
a)
Đặt
Ta có phương trình:
Phương trình có nên có hai nghiệm (đều thỏa mãn)
Với
Với
Vậy phương trình đã cho có 4 nghiệm phân biêt.
b)
Đặt
Ta có phương trình :
Với
Vậy phương trình đã cho có 2 nghiệm phân biệt.
c)
Đặt
Ta có phương trình :
Vậy phương trình vô nghiệm
Bài 57 trang 63 SGK Toán 9 tập 2: Giải các phương trình:
a)
b)
c)
d)
e)
f)
Phương pháp giải:
Đưa phương trình đã cho về dạng: . Sau đó sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn để tìm nghiệm.
Lời giải:
a)
Phương trình có nên có 2 nghiệm
b)
Vậy phương trình có 2 nghiệm phân biệt
c)
Điều kiện:
Ta có
Phương trình trên có nên có hai nghiệm (thỏa mãn)
Vậy phương trình đã cho có hai nghiệm .
d)
ĐKXĐ:
Vậy phương trình đã cho có 1 nghiệm duy nhất:
e)
Vậy phương trình đã cho có 2 nghiệm phân biệt.
f)
Vậy phương trình đã cho có 2 nghiệm phân biệt.
Bài 58 trang 63 SGK Toán 9 tập 2: Giải các phương trình:
a) ;b)
Phương pháp giải:
Phân tích vế trái của phương trình thành nhân tử sau đó đưa phương trình về dạng phương trình tích để giải:
Lời giải:
a)
Giải (*):
Ta có:
Vậy (*) có 2 nghiệm: ;
Vậy phương trình đã cho có 3 nghiệm:
b)
Vậy phương trình đã cho có 3 nghiệm:
Bài 59 trang 63 SGK Toán 9 tập 2: Giải các phương trình bằng cách đặt ẩn phụ:
a)
b)
Phương pháp giải:
a) Đặt để đưa phương trình đã cho về phương trình bậc hai ẩn
b) Đặt để đưa phương trình đã cho về phương trình bậc hai ẩn
Lời giải:
a) Đặt , ta thu được phương trình
Phương trình trên có nên có hai nghiệm
+ Với
+ Với
Vậy phương trình đã cho có ba nghiệm
b) ĐK:
Đặt , ta thu được phương trình
Phương trình trên có nên có hai nghiệm
+ Với .
Xét nên phương trình vô nghiệm.
+ Với
Phương trình (*) có nên có hai nghiệm (thỏa mãn)
Vậy phương trình đã cho có hai nghiệm .
Bài 60 trang 64 SGK Toán 9 tập 2: Với mỗi phương trình sau, đã biết một nghiệm (ghi kèm theo), hãy tìm nghiệm kia:
a)
b)
c)
d)
Phương pháp giải:
Phương pháp: Sử dụng hệ thức Viet để tìm nghiệm còn lại của phương trình:
Lời giải:
a)
Ta có:
b)
Ta có:
c)
Ta có:
d)
Vì là một nghiệm của pt (1) nên
Khi ta có: (hệ thức Vi-ét)
(vì và )
Bài 61 trang 64 SGK Toán 9 tập 2: Tìm hai số u và v trong mỗi trường hợp sau:
a) ; và
b)
Phương pháp giải:
Nếu S là tổng 2 số u, v; P là tích 2 số u, v thỏa mãn điều kiện thi u, v sẽ là nghiệm của phương trình sau:
Lời giải:
a) và
Ta có:
Nên và là hai nghiệm của phương trình:
Vì nên suy ra
b)
Ta có:
Nên và không có giá trị nào thỏa mãn đầu bài.
Bài 62 trang 64 SGK Toán 9 tập 2: Cho phương trình
a) Với giá trị nào của thì phương trình có nghiệm?
Phương pháp giải:
a)Phương trình có nghiệm khi và chỉ khi (hoặc
b) Hệ thức Vi-et: Với là hai nghiệm của phương trình thì
Biến đổi để sử dụng được hệ thức Vi-ét.
Lời giải:
a) Xét phương trình (1) có
Phương trình (1) có nghiệm khi
Ta có: với mọi
Vậy phương trình (1) luôn luôn có nghiệm với mọi giá trị của
Trong trường hợp phương trình có nghiệm, dùng hệ thức Vi-ét, hãy tính tổng các bình phương hai nghiệm của phương trình theo .
b) Xét phương trình (1) có
Gọi là hai nghiệm của phương trình (1)
Theo hệ thức Viet ta có:
Ta có:
Vậy .
Bài 63 trang 64 SGK Toán 9 tập 2: Sau hai năm, số dân của một thành phố tăng từ người lên người. Hỏi trung bình mỗi năm dân số của thành phố đó tăng bao nhiêu phần trăm?
Phương pháp giải:
Bước 1: Lập phương trình
1) Chọn ẩn và tìm điều kiện của ẩn (thông thường ẩn là đại lượng bài toán yêu cầu tìm)
2) Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết
3) Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình, đối chiếu với điều kiện ban đầu và kết luận.
Lời giải:
Gọi tỉ lệ tăng dân số trung bình mỗi năm là % .
Sau một năm dân số của thành phố là:
(người)
Sau hai năm, dân số của thành phố là:
(người)
Ta có phương trình:
Vậy phương trình có 2 nghiệm:
(loại)
Tỉ lệ tăng dẫn số trung bình hàng năm của thành phố là %
Bài 64 trang 64 SGK Toán 9 tập 2: Bài toán yêu cầu tìm tích của một số dương với một số lớn hơn nó 2 đơn vị, nhưng bạn Quân nhầm đầu bài lại tính tích của một số dương với một số bé hơn nó 2 đơn vị. Kết quả của bạn Quân là 120. Hỏi nếu làm đúng đầu bài đã cho thì kết quả phải là bao nhiêu?
Phương pháp giải:
Bước 1: Lập phương trình
1) Chọn ẩn và tìm điều kiện của ẩn (thông thường ẩn là đại lượng bài toán yêu cầu tìm)
2) Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết
3) Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình, đối chiếu với điều kiện ban đầu và kết luận.
Lời giải:
Gọi là số dương mà đầu bài cho,
Bạn Quân đã chọn số để nhân với .
Theo đề bài, ta có: hay
Phương trình trên có
Suy ra (thỏa mãn) hoặc (loại)
Nên số đầu bài cho là
Theo đầu bài yêu cầu tìm tích của với
Vậy kết quả đúng phải là:
Bài 65 trang 64 SGK Toán 9 tập 2: Một xe lửa đi từ Hà Nội vào Bình Sơn (Quảng Ngãi). Sau đó 1 giờ, một xe lửa khác đi từ Bình Sơn ra Hà Nội với vận tốc lớn hơn vận tốc của xe lửa thứ nhất là 5km/h. Hai xe gặp nhau tại một ga ở chính giữa quãng đường. Tìm vận tốc của mỗi xe, giả thiết rằng quãng đường Hà Nội – Bình Sơn dài 900km.
Phương pháp giải:
Bước 1: Lập phương trình
1) Chọn ẩn và tìm điều kiện của ẩn (thông thường ẩn là đại lượng bài toán yêu cầu tìm)
2) Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết
3) Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình, đối chiếu với điều kiện ban đầu và kết luận.
Lời giải:
Gọi (km/h) là vận tốc của xe lửa thứ nhất. Điều kiện .
Khi đó vận tốc của xe lửa thứ hai là (km/h).
Đến khi gặp nhau tại chính giữa quang đường thì mỗi xe đều đi được km.
Thời gian xe lửa thứ nhất đi từ Hà Nội đến chỗ gặp nhau là: (giờ)
Thời gian xe lửa thứ hai đi từ Bình Sơn đến chỗ gặp nhau là: (giờ)
Vì xe lửa thứ hai đi sau giờ, nghĩa là thời gian đi đến chỗ gặp nhau ít hơn xe thứ nhất giờ. Ta có phương trình:
Từ đó ta có: (nhận); (loại)
Vậy: Vận tốc của xe lửa thứ nhất là km/h
Vận tốc của xe lửa thứ hai là km/h.
Bài 66 trang 64 SGK Toán 9 tập 2: Cho tam giác ABC có BC = 16cm , đường cao AH = 12 cm. Một hình chữ nhật MNPQ có đỉnh M thuộc cạnh AB, đỉnh N thuộc cạnh AC còn hai đỉnh P và Q thuộc cạnh BC (h.17). Xác định vị trí của điểm M trên cạnh AB sao cho diện tích của hình chữ nhật đó bằng 36cm2.
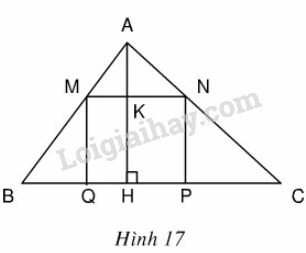
Phương pháp giải:
Giải bài toán bằng cách lập phương trình
Bước 1: Lập phương trình
1) Chọn ẩn và tìm điều kiện của ẩn (thông thường ẩn là đại lượng bài toán yêu cầu tìm)
2) Biểu thị các đại lượng chưa biết theo ẩn và các đại lượng đã biết
3) Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình, đối chiếu với điều kiện ban đầu và kết luận.
Chú ý: Dựa vào tỉ lệ cạnh của tam giác đồng dạng để tính các cạnh cần thiết.
Sử dụng công thức tính diện tích hình chữ nhật bằng tích của chiều dài với chiều rộng.
Lời giải:
Gọi (cm) là độ dài của đoạn . Điều kiện
Vì đồng dạng nên
Ta có:
Do đó diện tich hình chữ nhật là:
Ta có phương trình:
Phương tình trên có
Suy ra (nhận) hoặc (nhận)
Vậy độ dài của đoạn hoặc . Suy ra hoặc
Khi đó sẽ có hai vị trí trên nhưng diện tích hình chữ nhật luôn bằng cm2

