LG a

Giải phương trình

Phương pháp giải:

Giải phương trình bằng cách sử dụng

+) Xét phương trình bậc hai: $a{x}^2+bx+c=0(a\ne 0).$

 Nếu phương trình có $a-b+c=0$ thì phương trình có một nghiệm là $x_1=-1,$ nghiệm kia là $x_2=-{\displaystyle \frac{c}{a}}.$

Trả lời:

Xét phương trình $x^2-x-2=0$ có $a-b+c=1-\left(-1\right)+\left(-2\right)=0$ nên có hai nghiệm $x_1=-1;x_2=2.$

LG b

Vẽ hai đồ thị: $y=x^2$ và $y=x+2$ trong cùng một hệ trục tọa độ

Phương pháp giải:

Lập bảng giá trị rồi vẽ hai đồ thị hàm số $y=x^2;y=x+2$

Trả lời:

(h17)

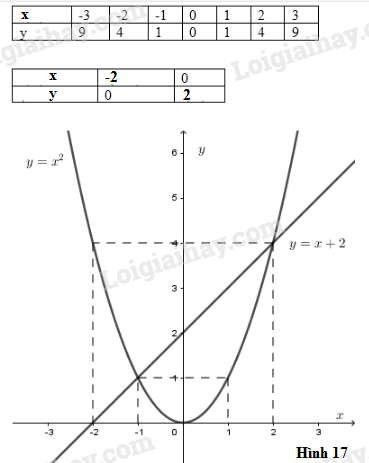
LG a

$5x^2-3x+1=2x+11$

Phương pháp giải:

Đưa phương trình đã cho về dạng: $a{x}^2+bx+c=0(a\ne 0)$ Sau đó sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn để tìm nghiệm.

Trả lời:

$5x^2-3x+1=2x+11$

$\begin{array}{l}\iff 5x^2-3x+1-2x-11=0\\ \iff 5x^2-5x-10=0\\ \iff x^2-x-2=0\end{array}$

Phương trình trên có $a-b+c=1-\left(-1\right)+\left(-2\right)=0$ nên có hai nghiệm $x_1=-1;x_2=2.$ 

LG b

${\displaystyle \frac{x^2}{5}}-{\displaystyle \frac{2x}{3}}={\displaystyle \frac{x+5}{6}}$

Phương pháp giải:

Đưa phương trình đã cho về dạng: $a{x}^2+bx+c=0(a\ne 0)$ Sau đó sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn để tìm nghiệm.

Trả lời:

${\displaystyle \frac{x^2}{5}}-{\displaystyle \frac{2x}{3}}={\displaystyle \frac{x+5}{6}}$

$\iff 6x^2-20x=5\left(x+5\right)$

$\iff 6x^2-25x-25=0$

Xét $\mathrm{\Delta }={\left(-25\right)}^2-\mathrm{4.6.}\left(-25\right)=1225>0$$\Rightarrow \sqrt{\mathrm{\Delta }}=35$

Nên phương trình có hai nghiệm $[\begin{array}{l}x={\displaystyle \frac{25+35}{2.6}}=5\\ x={\displaystyle \frac{25-35}{2.6}}={\displaystyle \frac{-5}{6}}\end{array}$

LG c

${\displaystyle \frac{x}{x-2}}={\displaystyle \frac{10-2x}{x^2-2x}}$ 

Phương pháp giải:

Sử dụng cách giải phương trình chứa ẩn ở mẫu

Chú ý: Phương trình tích $A\left(x\right).B\left(x\right)=0\iff [\begin{array}{l}A\left(x\right)=0\\ B\left(x\right)=0\end{array}$  

Trả lời:

Điều kiện: $x\ne \left\{0;2\right\}$

Ta có ${\displaystyle \frac{x}{x-2}}={\displaystyle \frac{10-2x}{x^2-2x}}$

$\iff {\displaystyle \frac{x}{x-2}}={\displaystyle \frac{10-2x}{x\left(x-2\right)}}$

$\begin{array}{l}\iff {\displaystyle \frac{x^2}{x\left(x-2\right)}}={\displaystyle \frac{10-2x}{x\left(x-2\right)}}\\ \Rightarrow x^2=10-2x\\ \iff x^2+2x-10=0\end{array}$

Phương trình trên có ${\mathrm{\Delta }}^{\prime }=1^2-1.\left(-10\right)=11>0$  nên có hai nghiệm $[\begin{array}{l}x=-1+\sqrt{11}\\ x=-1-\sqrt{11}\end{array}$  (thỏa mãn)

Vậy phương trình đã cho có hai nghiệm $x=-1+\sqrt{11};x=-1-\sqrt{11}$ .

LG d

${\displaystyle \frac{x+0,5}{3x+1}}={\displaystyle \frac{7x+2}{9x^2-1}}$

Phương pháp giải:

Sử dụng cách giải phương trình chứa ẩn ở mẫu

Chú ý: Phương trình tích $A\left(x\right).B\left(x\right)=0\iff [\begin{array}{l}A\left(x\right)=0\\ B\left(x\right)=0\end{array}$  

Trả lời:

Điều kiện: $x\ne \left\{-{\displaystyle \frac{1}{3}};{\displaystyle \frac{1}{3}}\right\}$

${\displaystyle \frac{x+0,5}{3x+1}}={\displaystyle \frac{7x+2}{9x^2-1}}$ $\iff {\displaystyle \frac{\left(x+0,5\right)\left(3x-1\right)}{\left(3x+1\right)\left(3x-1\right)}}={\displaystyle \frac{7x+2}{\left(3x-1\right)\left(3x+1\right)}}$

Khử mẫu và biến đổi, ta được

$\begin{array}{l}\Rightarrow 3x^2-x+1,5x-0,5=7x+2\\ \iff 3x^2-6,5x-2,5=0\\ \iff 6x^2-13x-5=0\end{array}$

Phương trình trên có $\mathrm{\Delta }={\left(-13\right)}^2-\mathrm{4.6.}\left(-5\right)=289>0$$\Rightarrow \sqrt{\mathrm{\Delta }}=17$  nên có hai nghiệm $x_1={\displaystyle \frac{13+17}{2.6}}={\displaystyle \frac{5}{2}};$ $x_2={\displaystyle \frac{13-17}{2.6}}=-{\displaystyle \frac{1}{3}}$

$x_2=-{\displaystyle \frac{1}{3}}$ không thỏa mãn điều kiện của ẩn

Vậy phương trình có một nghiệm $x={\displaystyle \frac{5}{2}}.$

LG e

$2\sqrt{3}{x}^2+x+1=\sqrt{3}\left(x+1\right)$

Phương pháp giải:

Đưa phương trình đã cho về dạng: $a{x}^2+bx+c=0(a\ne 0)$ Sau đó sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn để tìm nghiệm.

Trả lời:

$2\sqrt{3}{x}^2+x+1=\sqrt{3}\left(x+1\right)$

$\begin{array}{l}\iff 2\sqrt{3}{x}^2+x+1-\sqrt{3}\left(x+1\right)=0\\ \iff 2\sqrt{3}{x}^2+x+1-\sqrt{3}x-\sqrt{3}=0\\ \iff 2\sqrt{3}{x}^2+\left(1-\sqrt{3}\right)x+1-\sqrt{3}=0\end{array}$

$\mathrm{\Delta }={\left(1-\sqrt{3}\right)}^2-4.2\sqrt{3}\left(1-\sqrt{3}\right)$$=4-2\sqrt{3}-8\sqrt{3}+24$$=28-10\sqrt{3}$$=25-\mathrm{2.5.}\sqrt{3}+3$$={\left(5-\sqrt{3}\right)}^2$$\Rightarrow \sqrt{\mathrm{\Delta }}=5-\sqrt{3}$ 

$x_1={\displaystyle \frac{\sqrt{3}-1+5-\sqrt{3}}{4\sqrt{3}}}$$={\displaystyle \frac{\sqrt{3}}{3}};$$x_2={\displaystyle \frac{\sqrt{3}-1-5+\sqrt{3}}{4\sqrt{3}}}$$={\displaystyle \frac{1-\sqrt{3}}{2}}$

LG f

$x^2+2\sqrt{2}x+4=3\left(x+\sqrt{2}\right)$

Phương pháp giải:

Đưa phương trình đã cho về dạng: $a{x}^2+bx+c=0(a\ne 0)$ Sau đó sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn để tìm nghiệm.

Trả lời:

$x^2+2\sqrt{2}x+4=3\left(x+\sqrt{2}\right)$

$\begin{array}{l}\iff x^2+2\sqrt{2}x+4-3\left(x+\sqrt{2}\right)=0\\ \iff x^2+\left(2\sqrt{2}-3\right)x+4-3\sqrt{2}=0\end{array}$

Phương trình trên có $\mathrm{\Delta }={\left(2\sqrt{2}-3\right)}^2-\mathrm{4.1.}\left(4-3\sqrt{2}\right)$$=17-12\sqrt{2}-16+12\sqrt{2}=1>0$ nên phương trình có hai nghiệm $x_1=2-\sqrt{2};x_2=1-\sqrt{2}$

LG a

$1,2x^3-x^2-0,2x=0$

Phương pháp giải:

Biến đổi đưa về dạng phương trình tích $A\left(x\right).B\left(x\right)=0\iff [\begin{array}{l}A\left(x\right)=0\\ B\left(x\right)=0\end{array}$

Trả lời:

$1,2x^3-x^2-0,2x=0$

$\begin{array}{l}\iff x\left(1,2x^2-x-0,2\right)=0\\ \iff [\begin{array}{l}x=0\\ 1,2x^2-x-0,2=0(\ast )\end{array}\end{array}$

Phương trình (*) có $a+b+c=1,2+\left(-1\right)+\left(-0,2\right)=0$ nên có hai nghiệm $x=1;x={\displaystyle \frac{-0,2}{1,2}}=-{\displaystyle \frac{1}{6}}$

Vậy phương trình đã cho có ba nghiệm $x=0;x=1;x=-{\displaystyle \frac{1}{6}}.$

LG b

$5x^3-x^2-5x+1=0$  

Phương pháp giải:

Biến đổi đưa về dạng phương trình tích $A\left(x\right).B\left(x\right)=0\iff [\begin{array}{l}A\left(x\right)=0\\ B\left(x\right)=0\end{array}$

Trả lời:

$5x^3-x^2-5x+1=0$

$\begin{array}{l}\iff x^2\left(5x-1\right)-\left(5x-1\right)=0\\ \iff \left(x^2-1\right)\left(5x-1\right)=0\\ \iff [\begin{array}{l}{x}^2-1=0\\ 5x-1=0\end{array}\\ \iff [\begin{array}{l}x=1\\ x=-1\\ x={\displaystyle \frac{1}{5}}\end{array}\end{array}$

LG a

$3x^4-12x^2+9=0$

Phương pháp giải:

+)  Phương trình trùng phương $a{x}^4+b{x}^2+c=0(a\ne 0)$

+) Cách giải: Đặt ẩn phụ $t=x^2(t\ge 0)$ để đưa phương trình về phương trình bậc hai:  $a{t}^2+bt+c=0(a\ne 0).$

Trả lời:

Đặt $t=x^2(t\ge 0)$, ta được phương trình $3t^2-12t+9=0$

Phương trình trên có $a+b+c=3+\left(-12\right)+9=0$ nên có hai nghiệm $t=1;t=3$ (thỏa mãn)

+ Với $t=1\Rightarrow x^2=1\iff [\begin{array}{l}x=1\\ x=-1\end{array}$

+ Với $t=3\Rightarrow x^2=3\iff [\begin{array}{l}x=\sqrt{3}\\ x=-\sqrt{3}\end{array}$

Vậy phương trình đã cho có nghiệm $x=1;x=-1;x=\sqrt{3};x=-\sqrt{3}$.

LG b

$2x^4+3x^2-2=0$

Phương pháp giải:

+)  Phương trình trùng phương $a{x}^4+b{x}^2+c=0(a\ne 0)$

+) Cách giải: Đặt ẩn phụ $t=x^2(t\ge 0)$ để đưa phương trình về phương trình bậc hai:  $a{t}^2+bt+c=0(a\ne 0).$

Trả lời:

Đặt $t=x^2;t\ge 0$, ta có $2t^2+3t-2=0$

Phương trình trên có $\mathrm{\Delta }=3^2-\mathrm{4.2.}\left(-2\right)=25>0$$\Rightarrow \sqrt{\mathrm{\Delta }}=5$

$t_1={\displaystyle \frac{-3+5}{2.2}}={\displaystyle \frac{1}{2}}\left(N\right);$ $t_2={\displaystyle \frac{-3-5}{2.2}}=-2\left(L\right)$

Với $t=t_1={\displaystyle \frac{1}{2}}$ ta có $x^2={\displaystyle \frac{1}{2}}$$\iff x=\pm {\displaystyle \frac{\sqrt{2}}{2}}$

Vậy phương trình có nghiệm $x={\displaystyle \frac{\sqrt{2}}{2}};$$x=-{\displaystyle \frac{\sqrt{2}}{2}}$ .

LG c

$x^4+5x^2+1=0$ 

Phương pháp giải:

LG a

$2{\left(x^2-2x\right)}^2+3\left(x^2-2x\right)+1=0$

Phương pháp giải:

Đặt $x^2-2x=t$ để đưa phương trình đã cho về phương trình bậc hai ẩn $t.$

Trả lời:

Đặt $x^2-2x=t$, ta có $2t^2+3t+1=0$ 

Phương trình trên có $a-b+c=2-3+1=0$ nên có hai nghiệm $t=-1;t=-{\displaystyle \frac{1}{2}}.$

+ Với $t=-1$ ta có $x^2-2x=-1\iff x^2-2x+1=0$

Phương trình này có $a+b+c=1+\left(-2\right)+1=0$ nên có nghiệm $x_1=x_2=1$

+ Với $t=-{\displaystyle \frac{1}{2}}$ ta có $x^2-2x=-{\displaystyle \frac{1}{2}}$$\iff x^2-2x+1={\displaystyle \frac{1}{2}}$$\iff {\left(x-1\right)}^2={\displaystyle \frac{1}{2}}$

$\iff [\begin{array}{l}x-1={\displaystyle \frac{\sqrt{2}}{2}}\\ x-1=-{\displaystyle \frac{\sqrt{2}}{2}}\end{array}\iff [\begin{array}{l}x={\displaystyle \frac{2+\sqrt{2}}{2}}\\ x={\displaystyle \frac{2-\sqrt{2}}{2}}\end{array}$

Vậy phương trình đã cho có ba nghiệm $x=1;x={\displaystyle \frac{2+\sqrt{2}}{2}};x={\displaystyle \frac{2-\sqrt{2}}{2}}$

LG b

${\left(x+{\displaystyle \frac{1}{x}}\right)}^2-4\left(x+{\displaystyle \frac{1}{x}}\right)+3=0$

Phương pháp giải:

Đặt $x+{\displaystyle \frac{1}{x}}=t$ để đưa phương trình đã cho về phương trình bậc hai ẩn $t.$ 

Trả lời:

ĐK: $x\ne 0.$

Đặt $x+{\displaystyle \frac{1}{x}}=t$, ta thu được phương trình $t^2-4t+3=0$

Phương trình trên có $a+b+c=1+\left(-4\right)+3=0$ nên có hai nghiệm $t=1;t=3.$

+ Với $t=1\Rightarrow x+{\displaystyle \frac{1}{x}}=1$$\Rightarrow x^2-x+1=0$ . Xét $\mathrm{\Delta }={\left(-1\right)}^2-\mathrm{4.1.1}=-3<0$ nên phương trình vô nghiệm.

+ Với $t=3\Rightarrow x+{\displaystyle \frac{1}{x}}=3$$\Rightarrow x^2-3x+1=0$ (*)

Phương trình (*) có $\mathrm{\Delta }={\left(-3\right)}^2-\mathrm{4.1.1}=5>0$ nên có hai nghiệm $[\begin{array}{l}x={\displaystyle \frac{3+\sqrt{5}}{2}}\\ x={\displaystyle \frac{3-\sqrt{5}}{2}}\end{array}$ (thỏa mãn)

Vậy phương trình đã cho có hai nghiệm $x={\displaystyle \frac{3+\sqrt{5}}{2}};x={\displaystyle \frac{3-\sqrt{5}}{2}}$

LG a

Biết u + v = 12, uv = 28 và u > v

Phương pháp giải:

Ta sử dụng: Nếu hai số có tổng bằng $S$ và tích bằng $P$ thì hai số đó là hai nghiệm của phương trình $X^2-SX+P=0$ (ĐK: $S^2\ge 4P$)

Trả lời:

Hai số phải tìm là hai nghiệm của phương trình $x^2-12x+28=0$

Phương trình trên có ${\mathrm{\Delta }}^{\prime }={\left(-6\right)}^2-1.28=8>0$$\Rightarrow \sqrt{{\mathrm{\Delta }}^{\prime }}=2\sqrt{2}$  nên có hai nghiệm $x_1=6+2\sqrt{2};$ $x_2=6-2\sqrt{2}$

Vì $u>v$ nên phải chọn $u=6+2\sqrt{2};v=6-2\sqrt{2}$ .

LG b

u + v = 3, uv = 6 

Phương pháp giải:

Ta sử dụng: Nếu hai số có tổng bằng $S$ và tích bằng $P$ thì hai số đó là hai nghiệm của phương trình $X^2-SX+P=0$ (ĐK: $S^2\ge 4P$)

Trả lời:

Hai số phải tìm là hai nghiệm của phương trình $x^2-3x+6=0$

Phương trình trên có $\mathrm{\Delta }=(-3{)}^2-\mathrm{4.1.6}=-15<0$  nên phương trình vô nghiệm.

Vậy không có hai số $u,v$ thỏa mãn yêu cầu đề bài.