Toptailieu.vn xin giới thiệu 47 câu trắc nghiệm Các khái niệm mở đầu Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

47 câu trắc nghiệm Các khái niệm mở đầu Kết nối tri thức (có đáp án 2023) CHỌN LỌC

Lý thuyết

1. KHÁI NIỆM VECTƠ

+) Vecto là một đoạn thẳng có hướng.

Ví dụ 1: i) vecto : (đọc là vecto AB)   

ii) Vecto : 

iii) vecto : 

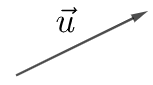
+) Độ dài của vecto là khoảng cách giữa điểm đầu và điểm cuối của vecto đó.

Kí hiệu: độ dài của vecto  là ||.

Ví dụ 2: || = AB; || = DE

+) Vecto không, là vecto có độ dài bằng 0. Ví dụ: , ,... (điểm đầu trùng điểm cuối)

Kí hiệu chung là .

2. HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG NHAU

+) Giá của vecto:  là đường thẳng đi qua điểm đầu và điểm cuối của vecto đó.

Ví dụ: Giá của vecto  là đường thẳng CD

+) Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

+) Hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng.

Ví dụ:

Ba vecto , ,  cùng phương.

Trong đó 2 vecto ,  cùng hướng, còn 2 vecto ,  ngược hướng.

+) Hai vecto được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng.

* Chú ý:

- Chỉ khi hai vecto cùng phương ta mới nói tới chúng cùng hướng hay ngược hướng.

- Vecto  cùng phương, cùng hướng với mọi vecto.

- Với mỗi điểm O và vecto  cho trước, có duy nhất điểm A sao cho  =

* Nhận xét:

+) Ba điểm A, B, C thẳng hàng khi và chỉ khi  và  cùng phương.

+) Ba điểm A, B, C thẳng hàng, B nằm giữa khi và chỉ khi  và  cùng hướng.

Bài tập

Câu 1: Nếu  thì:

A. tam giác ABC là tam giác cân                      B. tam giác ABC là tam giác đều

C. A là trung điểm đoạn BC                              D. điểm B trùng với điểm C

Lời giải

Đáp án D

⇒ B ≡ C

Câu 2: Cho ba điểm M, N, P thẳng hàng, trong đó N nằm giữa hai điểm M và P. Khi đó cặp vectơ nào sau đây cùng hướng?

Lời giải

Đáp án A

Câu 3: Cho tam giác ABC, có thể xác định được bao nhiêu vectơ khác vectơ-không có điểm đầu và điểm cuối là các đỉnh A, B, C?

A. 4                                     B. 6                        C. 9                        D. 12

Lời giải

Ta có các vectơ: 

Đáp án B.

Câu 4: Cho hai vectơ không cùng phương  và . Mệnh đề nào sau đây đúng

A. Không có vectơ nào cùng phương với cả hai vectơ  và 

B. Có vô số vectơ cùng phương với cả hai vectơ  và

C. Có một vectơ cùng phương với cả hai vectơ  và , đó là vectơ 

D. Cả A, B, C đều sai

Lời giải

Vì vectơ cùng phương với mọi vectơ. Nên có một vectơ cùng phương với cả hai vectơ và , đó là vectơ  .

Đáp án C.

Câu 5: Cho hình lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ không, cùng phương với vectơ  có điểm đầu và điểm cuối là các đỉnh của lục giác là

A. 4                                     B. 6                        C. 8                        D. 10

Lời giải

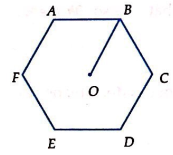
Các vectơ cùng phương với vectơ  là:

Đáp án B.

Câu 6: Điều kiện nào là điều kiện cần và đủ để 

A. ABCD là hình bình hành

B. ACBD là hình bình hành

C. AD và BC có cùng trung điểm

D. 

Lời giải

Đáp án C

Câu 7: Cho hình vuông ABCD, câu nào sau đây là đúng?

Lời giải

Đáp án D

Câu 8: Cho vectơ  và một điểm C. Có bao nhiêu điểm D thỏa mãn .

A. 1                                     B. 2                        C. 0                        D. Vô số

Lời giải

Đáp án A

Câu 9: Cho hình bình hành ABCD với O là giao điểm của hai đường chéo. Câu nào sau đây là sai?

Lời giải

Đáp án A

Câu 10: Cho tứ giác đều ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Mệnh đề nào sau đây là sai?

Lời giải

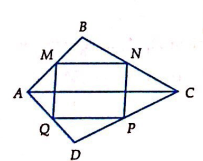
Ta có  (do cùng song song và bằng AC).

Do đó MNPQ là hình bình hành.

Đáp án D.

Câu 12: Cho ba điểm A, B, C phân biệt và thẳng hàng. Mệnh đề nào sau đây đúng?

A. =                                     B. và cùng hướng

C.  và ngược hướng            D.  và  cùng phương

Lời giải

Với ba trường hợp lần lượt A, B, C nằm giữa thì ta luôn có , cùng phương.

Đáp án D.

Câu 13: Cho tứ giác ABCD. Có bao nhiêu vectơ khác vectơ-không có điểm đầu và cuối là các đỉnh của tứ giác?

A. 4                                     B. 8                        C. 10                      D. 12

Lời giải

Đáp án D

Một vectơ khác vectơ không được xác định bởi 2 điểm phân biệt. Do đó có 12 cách chọn 2 điểm trong 4 điểm của tứ giác.

Câu 14: Cho 5 điểm A, B, C, D, E có bao nhiêu vectơ khác vectơ-không có điểm đầu là A và điểm cuối là một trong các điểm đã cho:

A. 4                                     B. 20                      C. 10                      D. 12

Lời giải

Đáp án A

Câu 15: Hai vectơ được gọi là bằng nhau khi và chỉ khi:

A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau

B. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành

C. Chúng trùng với một trong các cặp cạnh đối của một tam giác đều

D. Chúng cùng hướng và độ dài của chúng bằng nhau

Lời giải

Đáp án D

Câu 16: Cho lục giác đều ABCDEF tâm O. Hãy tìm các vectơ khác vectơ-không có điểm đầu, điểm cuối là đỉnh của lục giác và tâm O sao cho bằng với ?

Lời giải

Đáp án D

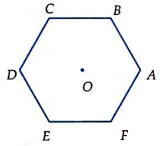
Các vectơ bằng vectơ  là:

Câu 18: Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của AB, BC, CA. Xác định các vectơ cùng phương với .

Lời giải

Đáp án C

Có 3 đường thẳng song song với MN là AC, AP, PC

Nên có 7 vectơ

Câu 20: Cho ba điểm A, B, C cùng nằm trên một đường thẳng. Các vectơ , cùng hướng khi và chỉ khi:

A. Điểm B thuộc đoạn AC  B. Điểm A thuộc đoạn BC

C. Điểm C thuộc đoạn AB  D. Điểm A nằm ngoài đoạn BC

Lời giải

Đáp án A

Câu 21: Cho tam giác đều cạnh 2a. Đẳng thức nào sau đây là đúng?

A.  =            B. = 2a                C. || = 2a              D. = AB

Lời giải

Đáp án C

Vì tam giác đều nên AB = || = 2a

Câu 22: Cho tam giác không cân ABC. Gọi H, O lần lượt là trực tâm, tâm đường tròn ngoại tiếp của tam giác. M là trung điểm của BC. Mệnh đề nào sau đây là đúng?

A. Tam giác ABC nhọn thì  cùng hướng.

B. luôn cùng hướng.

C. cùng phương nhưng ngược hướng.

D. có cùng giá

Lời giải

Đáp án A

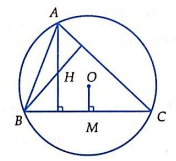
Thật vậy khi ΔABC nhọn thì ta có:

O, H nằm trong tam giác ⇒  cùng hướng

Câu 23: Cho hình thoi tâm O, cạnh bằng a và A = 60^o. Kết luận nào sau đây là đúng?

Lời giải

Đáp án A

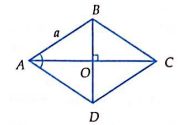
Vì A = 60^o ⇒ ΔABC đều ⇒ AO = 

Câu 24: Cho tứ giác ABCD. Gọi M, N, P lần lượt là trung điểm của AD, BC và AC. Biết . Chọn câu đúng.

Lời giải

Đáp án C

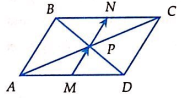
Ta có: MP // DC, MP = DC, PN // AB, PN = AB. Mà MP = PN

⇒  ⇒ ABCD là hình bình hành ⇒ 

Câu 25: Cho tam giác ABC với trực tâm H. D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây là đúng?

Lời giải

Ta có BD là đường kính ⇒ .

AH ⊥ BC, DC ⊥ BC ⇒ AH // DC (1)

Ta lại có CH ⊥ AB, DA ⊥ AB ⇒ CH // DA (2)

Từ (1) và (2) ⇒ tứ giác HADC là hình bình hành ⇒ .

Đáp án C.

Câu 26: Cho ΔABC với điểm M nằm trong tam giác. Gọi A', B', C' lần lượt là trung điểm của BC, CA, AB và N, P, Q lần lượt là các điểm đối xứng với M qua A', B', C'. Câu nào sau đây đúng?

Lời giải

Ta có AMCP là hình bình hành ⇒

Lại có AQBM và BMCN là hình bình hành

⇒ NC = BM = QA

⇒ AQNC là hình bình hành ⇒ .

Đáp án B.

Câu 27: Cho tam giác ABC có H là trực tâm và O là tâm đường tròn ngoại tiếp. Gọi D là điểm đối xứng với B qua O. Câu nào sau đây đúng?

Lời giải

Đáp án A

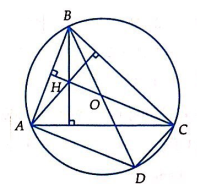
Ta có thể chỉ ra được ADCH là hình bình hành ⇒ 

Câu 28: Cho đường tròn tâm O. Từ điểm A nằm ngoài (O), kẻ hai tiếp tuyến AB, AC tới (O). Xét mệnh đề:

Mệnh đề đúng là:

A. Chỉ (I)                             B. (I) và (III)          C. (I), (II), (III)       D. Chỉ (III)

Lời giải

Đáp án D

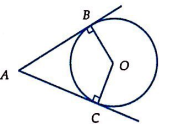
Ta có: OB = OC = R ⇒ 

Câu 29: Cho hình bình hành ABCD tâm O. Gọi P, Q, R lần lượt là trung điểm của AB, BC, AD. Lấy 8 điểm trên là gốc hoặc ngọn của các vectơ. Tìm mệnh đề sai?

A. Có 2 vectơ bằng       B. Có 4 vectơ bằng  

C. Có 2 vectơ bằng         D. Có 5 vectơ bằng 

Lời giải

Đáp án D

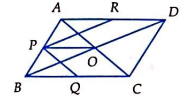
Ta có: 

Câu 30: Cho hình vuông ABCD tâm O cạnh a. Gọi M là trung điểm của AB, N là điểm đối xứng với C qua D. Hãy tính độ dài của vectơ .

Lời giải

Đáp án C

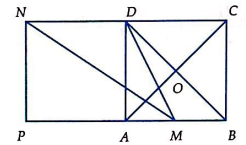
Áp dụng định lý Pytago trong tam giác vuông MAD ta có:

DM² = AM² + AD² = ()² + a²

= 

⇒ DM = 

Qua N kẻ đường thẳng song song với AD cắt AB tại P.

Khi đó tứ giác ADNP là hình vuông và PM = PA + AM = a +  = 

Áp dụng định lý Pytago trong tam giác vuông NPM ta có:

MN² = NP² + PM² = a² + ()²

= 

⇒ MN = 

Suy ra || = MN =

Câu 31: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Gọi O là giao điểm của các đường chéo của tứ giác MNPQ, trung điểm của các đoạn thẳng AC, BD tương ứng là I, J. Khẳng định nào sau đây là đúng?

Lời giải

Đáp án D

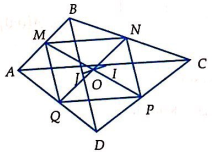
Ta có: MNPQ là hình bình hành ⇒  = 

Ta có:

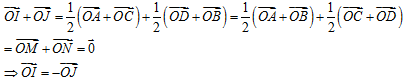
Câu 32: Cho khác  và cho điểm C, có bao nhiêu điểm D thỏa mãn || = ||.

A. vô số điểm.                     B. điểm.               C. điểm.              D. không có điểm nào.

Lời giải

Chọn A

|| = || ⇒ AB = CD. Mà AB là hằng số dương và C cố định cho trước nên D thuộc đường tròn tâm C bán kính là AB.

Câu 33: Cho 3 điểm M, N, P thẳng hàng trong đó N nằm giữa M và P. khi đó các cặp véc tơ nào sau đây cùng hướng?

Lời giải

Chọn A

Câu 34: Cho ba điểm M, N, P thẳng hàng, trong đó điểm N nằm giữa hai điểm M và P. Khi đó các cặp vectơ nào sau đây cùng hướng?

Lời giải

Chọn D

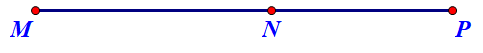
Cặp vectơ cùng hướng là và .

Câu 35: Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của AB, AC và BC. Có bao nhiêu véctơ khác véctơ không có điểm đầu và điểm cuối là các điểm trong các điểm A, B, C, M, N, P bằng véctơ (không kể véctơ )?

A. 1.                                    B. 4.                      C. 2.                      D. 3.

Lời giải

Chọn C

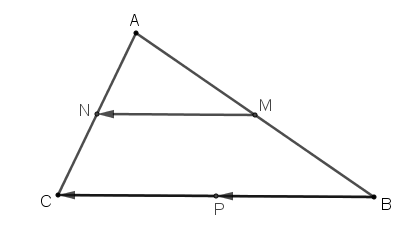
Các véctơ khác véctơ không có điểm đầu và điểm cuối là các điểm trong các điểm A, B, C, M, N, P bằng véctơ (không kể véctơ ) là:  và 

Câu 36: Cho hình thoi ABCD. Khẳng định nào sau đây đúng?

Lời giải

Chọn D

Câu 37: Hai vectơ được gọi là bằng nhau khi và chỉ khi

A. Chúng cùng phương và có độ dài bằng nhau.

B. Giá của chúng trùng với một trong các cặp cạnh đối của một hình bình hành.

C. Giá của chúng trùng nhau và độ dài của chúng bằng nhau.

D. Chúng cùng hướng và độ dài của chúng bằng nhau.

Lời giải

Chọn D

Câu 38: Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Đẳng thức nào sau đây sai?

Lời giải

Chọn D

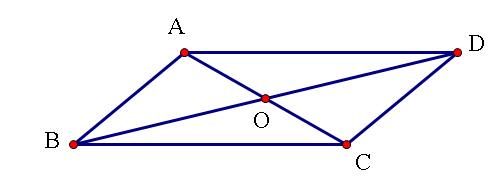
Ta có:  =  ≠ 

Câu 39: Cho lục giác đều ABCDEF tâm O. Ba vectơ bằng với là

Lời giải

Chọn B

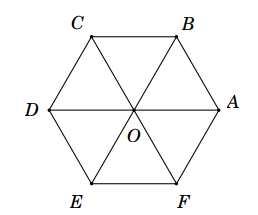
Ba vectơ bằng là .

Câu 40: Cho lục giác đều  ABCEF tâm O. Số các vectơ bằng OC có điểm đầu và điểm cuối là các đỉnh của lục giác là

A. 2.                                   B. 3.                      C. 46.                      D. .

Lời giải

Chọn A

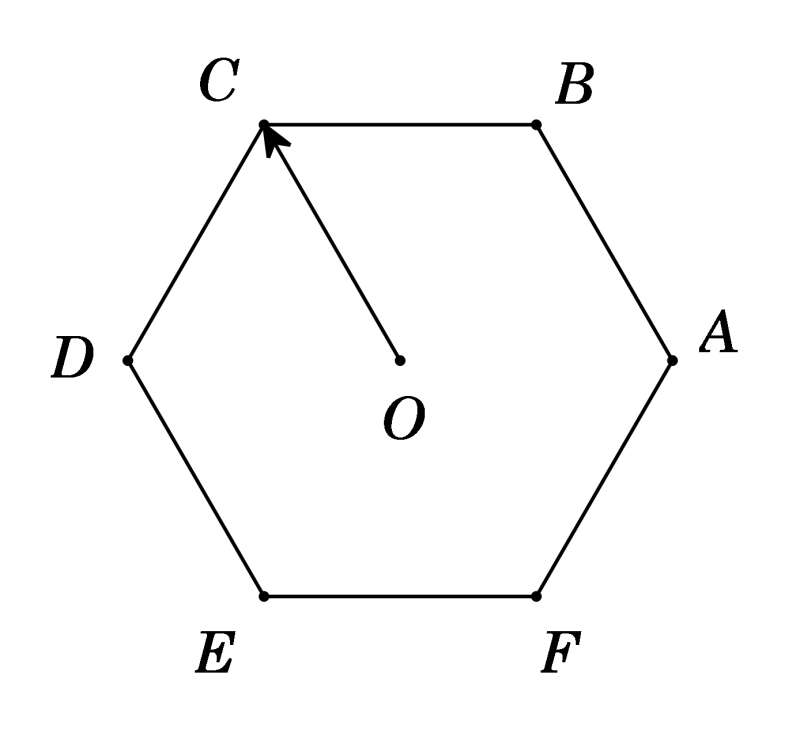
Đó là các vectơ: AB, ED.

Câu 41: Cho lục giác đều ABCDEF tâm O. Ba vectơ bằng vectơ là:

Lời giải

Chọn C

Giả sử lục giác đều ABCDEF tâm O có hình vẽ như sau

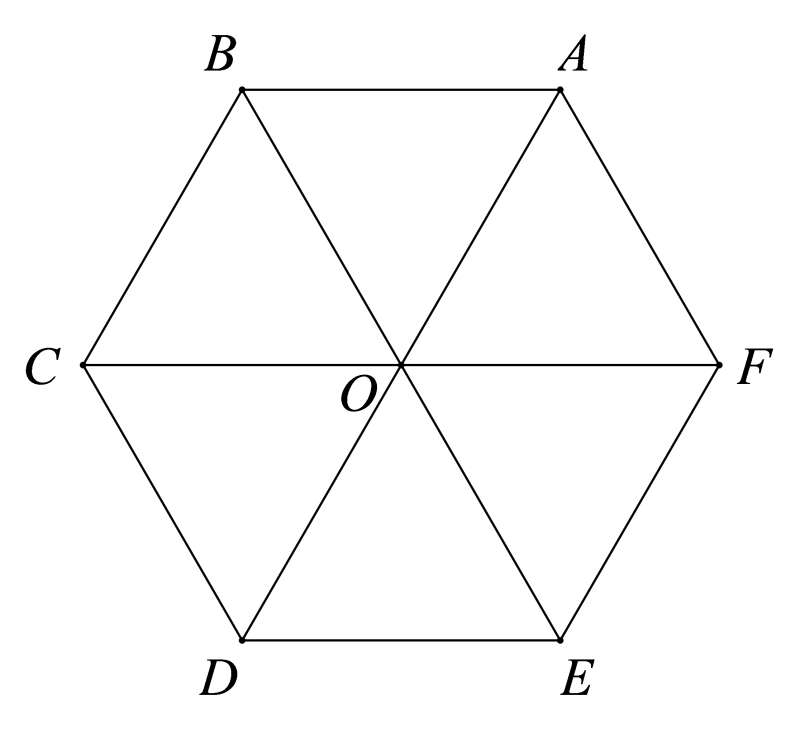
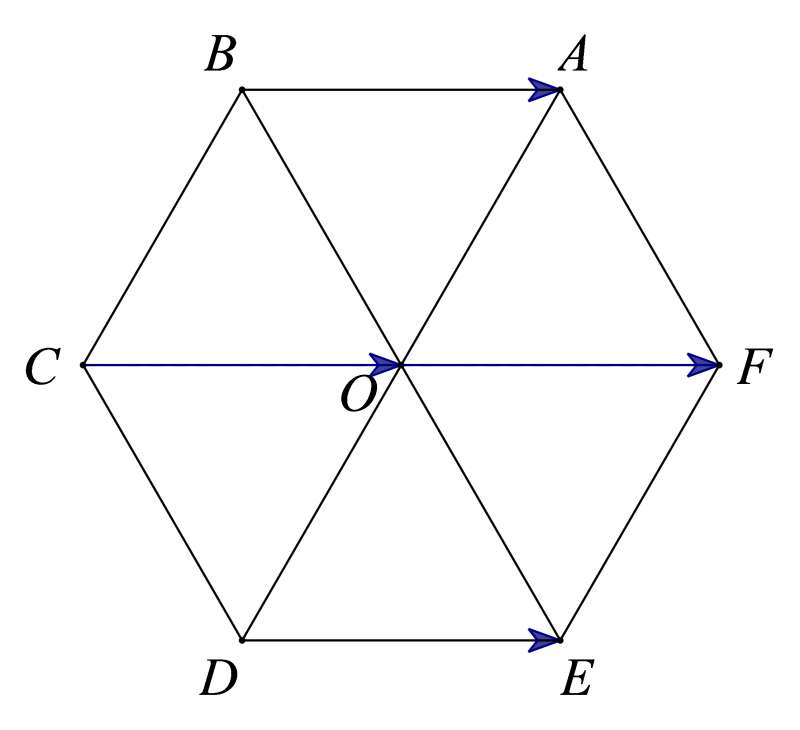
Dựa vào hình vẽ và tính chất của lục giác đều ta có các vectơ bằng vectơ  là .

Câu 42: Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của AB, AC và BC. Có bao nhiêu véctơ khác véctơ không có điểm đầu và điểm cuối là các điểm trong các điểm A, B, C, M, N, P bằng véctơ ?

A. 1.                                    B. 4.                      C. 2.                      D. 3

Lời giải

Chọn C

Các véctơ khác véctơ không có điểm đầu và điểm cuối là các điểm trong các điểm A, B, C, M, N, P bằng véctơ là: và 

Câu 46: Cho lục giác đều ABCDEF tâm O. Số vecto bằng vecto có điểm đầu và điểm cuối là các đỉnh của lục giác là

A. 6.                                   B. 3.                      C. 2.                      D. 4.

Lời giải

Chọn C

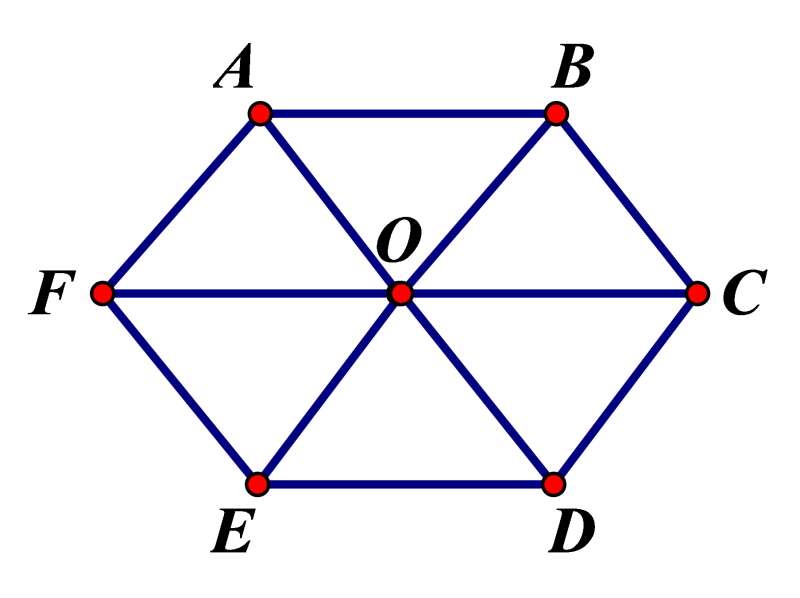
Các vecto bằng vecto mà điểm đầu, điểm cuối là các đỉnh của lục giác là , .

Câu 47: Cho tam giác ABC có trực tâm H và tâm đường tròn ngoại tiếp O. Gọi D là điểm đối xứng với A qua O; E là điểm đối xứng với O qua BC. Khẳng định nào sau đây là đúng?

Lời giải

Chọn B

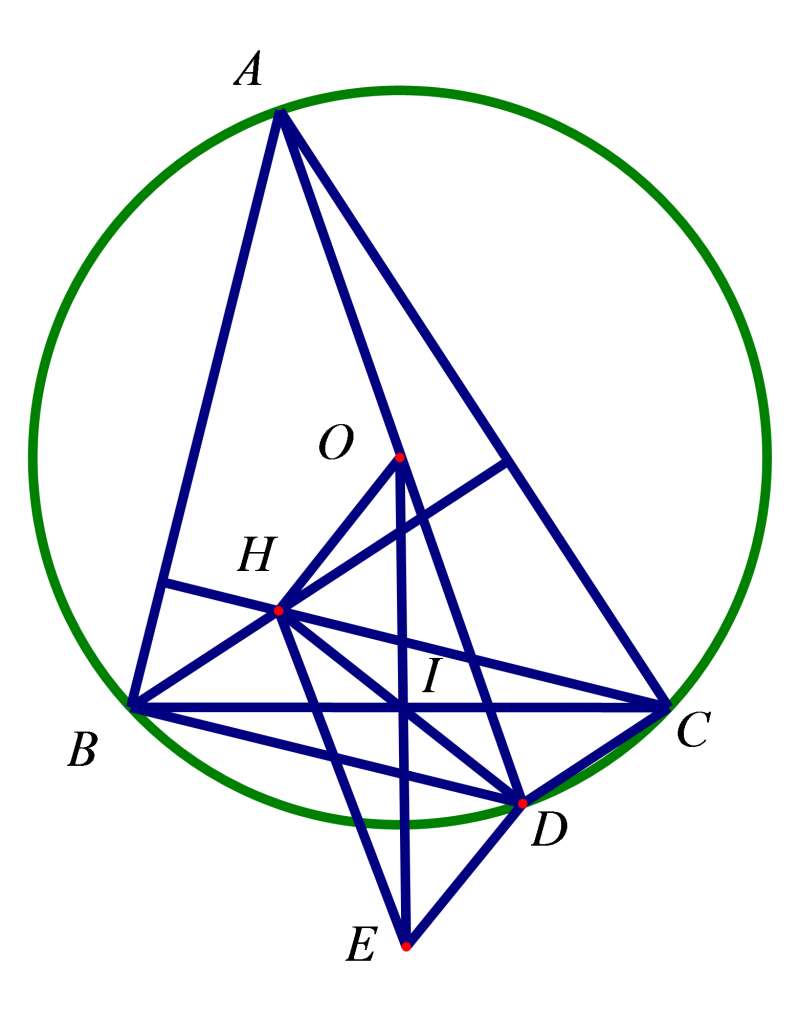
Gọi I là trung điểm của BC.

Do E là điểm đối xứng với O qua BC nên I là trung điểm của OE (1).

Ta có, CH // DB (cùng vuông góc với AB)

Tương tự, BH // DC (cùng vuông góc với AC)

Từ đó suy ra BHCD là hình bình hành nên I là trung điểm của HD(2).

Từ (1) và (2) suy ra, OHED là hình bình hành nên .

Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 3

Bài 8: Tổng và hiệu của hai vecto

Bài 9: Tích của một vecto với một số

Bài 10: Vecto trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vecto