Toptailieu.vn xin giới thiệu 16 câu trắc nghiệm Hàm số bậc hai Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
16 câu trắc nghiệm Hàm số bậc hai Kết nối tri thức (có đáp án 2023) CHỌN LỌC
Lý thuyết
1. Hàm số bậc hai
Định nghĩa
Hàm số bậc hai được cho bởi công thức:
y = ax2 + bx + c (a ≠ 0)
có tập xác định D = R và biệt thức Δ = b2 - 4ac
Chiều biến thiên:
Nếu a > 0 thì hàm số y = ax2 + bx + c:

Bảng biến thiên:
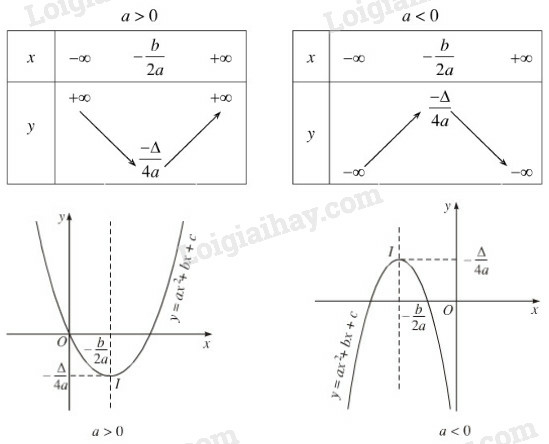
2. Đồ thị hàm số bậc hai
Đồ thị hàm số y = ax2 + bx + c (a ≠ 0) là đường parabol có:
+) đỉnh là điểm 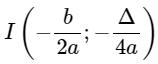
+) trục đối xứng là đường thẳng 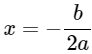 .
.
+) Bề lõm của Parabol quay lên trên nếu a > 0 và xuống dưới nếu a < 0.
+) Giao điểm với trục tung: A(0;c).
+) Hoành độ giao điểm với trục hoành (nếu có) là nghiệm của phương trình ax2 + bx + c = 0.
* Cách vẽ
Cách 1: (Dùng cho mọi trường hợp)
Bước 1: Xác định tọa độ đỉnh I
Bước 2: Vẽ trục đối xứng
Bước 3: Xác định tọa độ các giao điểm của Parabol cới trục tung và trục hoành (nếu có)
Bước 4: Vẽ parabol (lưu ý dấu của hệ số a - liên quan đến bề lõm của Parabol)
Cách 2: (sử dụng khi đã có đồ thị hàm số y = ax2)
Đồ thị hàm số y = ax2 + bx + c (a ≠ 0) suy ra từ đồ thị hàm số y = ax2 bằng cách:
+ Tịnh tiến song song với trục hoành |![]() | đơn vị về bên trái nếu
| đơn vị về bên trái nếu 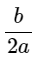 > 0, về bên phải nếu
> 0, về bên phải nếu 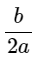 < 0.
< 0.
+ Tịnh tiến song song với trục tung |![]() | đơn vị lên trên nếu
| đơn vị lên trên nếu 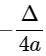 > 0, và xuống dưới nếu
> 0, và xuống dưới nếu 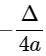 < 0.
< 0.
Bài tập
Câu 1: Đồ thị của hàm số y = 2x2 - x - 3.
a) Có trục đối xứng là:

b) Có tọa độ đỉnh là:
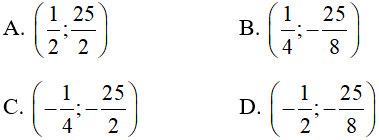
Đáp án
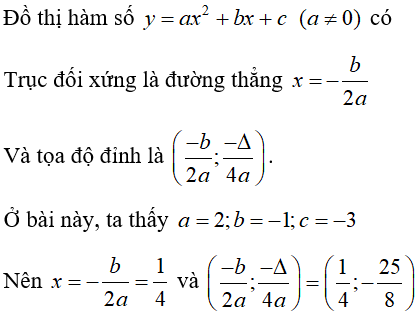
a) Chọn đáp án C
b) Chọn đáp án B
Câu 2: Parabol có đỉnh 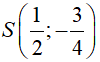 , quay bề lõm xuống dưới, đi qua điểm A(0; -1) là đồ thị của hàm số:
, quay bề lõm xuống dưới, đi qua điểm A(0; -1) là đồ thị của hàm số:
A. y = -x2 + x B. y = -x2 + x - 1
C. y = x2 + x - 1 D. y = -x2 + x + 1
Đáp án

Chọn đáp án B
Câu 3: Một hàm số bậc hai có đồ thị như hình bên.
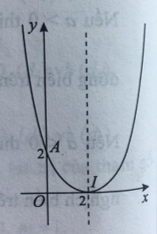
Công thức biểu diễn hàm số đó là:
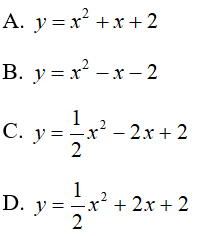
Đáp án
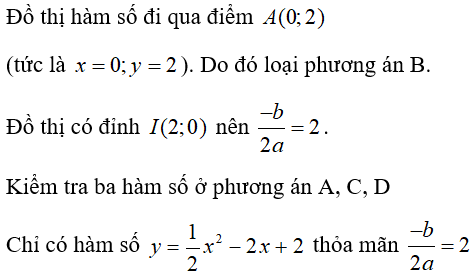
Chọn đáp án C
Câu 4: Xác định hàm số bậc hai y = ax2 - 3x + c biết rằng đồ thị của nó đi qua hai điểm A(2; 3) và B(-1; 6).
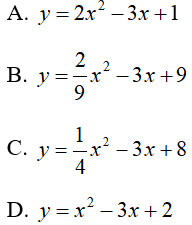
Đáp án
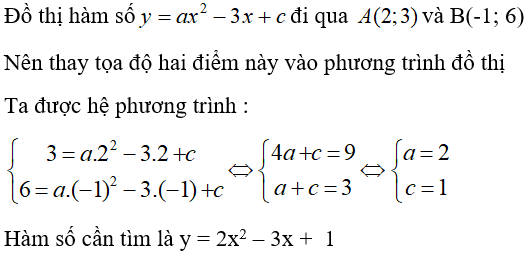
Chọn đáp án A

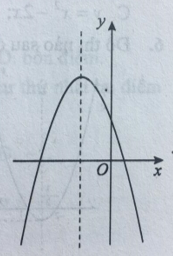
Câu 5: Xác định dấu của a, b, c nếu biết parabol y = ax2 + bx + c có dạng đồ thị như hình vẽ bên.
A. a > 0, b > 0, c < 0
B. a < 0, b > 0, c > 0
C. a < 0, b < 0, c > 0
D. a < 0, b < 0, c < 0
Đáp án
Quan sát hình vẽ thấy parabol quay bề lõm xuống dưới nên a < 0(loại phương án A);
Parabol cắt trục tung tại điểm có tung độ dương nên c > 0 (loại tiếp phương án D).
Chỉ còn phương án B hoặc C.
Hoành độ của tọa độ đỉnh mang dấu âm nên -b/2a < 0, mà a < 0 nên b < 0.
Chọn đáp án C
Câu 6: Trong các hàm số y = x2 - 2x + 1, y = -x2 - 2x + 1, y = x2 - 3x + 1 và y = -x2 + 4x + 1, có bao nhiêu hàm số đồng biến trên khoảng (3/2; 2)?
A. 1
B. 2
C. 3
D. 4
Đáp án

Chọn đáp án C
Câu 7: Parabol nào sau đây có đỉnh trùng với đỉnh của parabol (P): y = x2 + 4x?
A. y = 2x2 + 8x B. y = -x2 + 4x + 1
C. y = x2 + 4x + 1 D. y = 2x2 + 8x + 4
Đáp án
* Parabol (P): y = x2 + 4x có đỉnh là I(-2;-4)
* Phương án A có đỉnh (-2;-8).
* Phương án B có đỉnh (2;5)
* Phương án C có đỉnh (-2;-3)
* Phương án D có đỉnh (-2;-4)
Chọn đáp án D
Câu 8: Nếu parabol (P): y = ax2 + bx + c (a ≠ 0) có đỉnh nằm phía trên trục hoành và cắt trục hoành tại hai điểm thì:
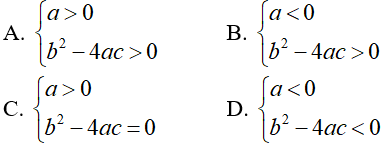
Đáp án

Chọn đáp án B
Câu 9: Hàm số nào sau đây có giá trị nhỏ nhất tại x = 5/4 ?
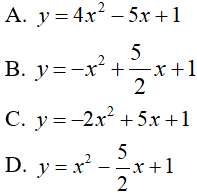
Đáp án
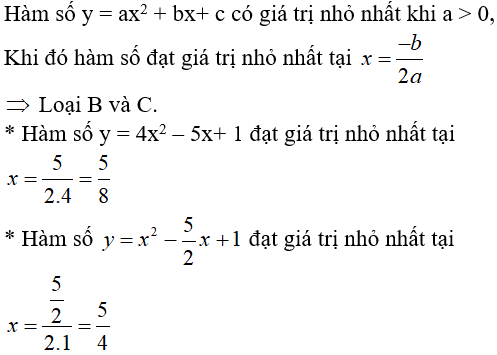
Chọn đáp án D
Câu 10: Một hàm số bậc hai có đồ thị như hình vẽ bên.
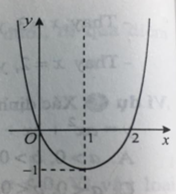
Công thức biểu diễn hàm số đó là:
A. y = -x2 + 2x B. y = -x2 + 2x + 1
C. y = x2 - 2x D. y = x2 - 2x + 1
Đáp án
Gọi phương trình của đồ thị hàm số là y = ax2 + bx + c.
Dựa vào hình vẽ, ta thấy đồ thị hàm số đi qua các điểm O(0; 0); (1; -1) và(2; 0).
Thay tọa độ các điểm này vào phương trình hàm số ta được hệ phương trình:
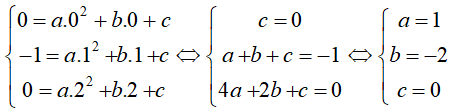
Phương trình đồ thị hàm số là y = x2 – 2x
Chọn đáp án C
Câu 11: Đồ thị nào sau đây là đồ thị của hàm số y = x2 - 3x + 2?
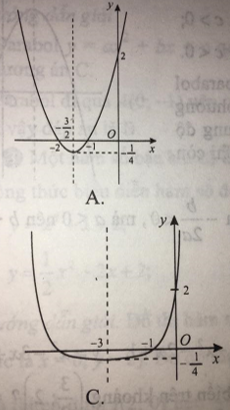
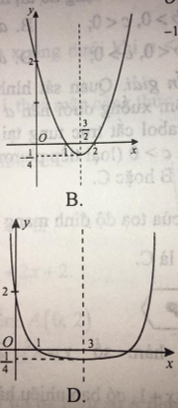
Đáp án
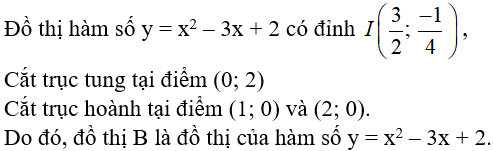
Chọn đáp án B
Câu 12: Nếu hàm số y = ax2 + bx + c có a > 0, b < 0, c < 0 thì đồ thị của nó có dạng nào trong các hình sau?
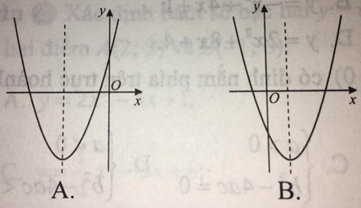
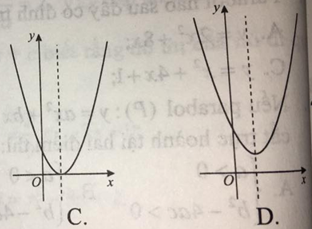
Đáp án

Chọn đáp án B
Câu 13: Gọi (P) là đồ thị hàm số y = ax2 + c. Để đỉnh của (P) có tọa độ (0; -3) và một trong hai giao điểm của (P) với trục hoành là điểm có hoành độ bằng -5 thì:
Đáp án
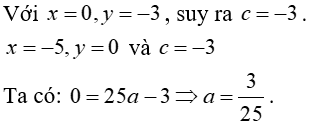
Chọn đáp án D
Câu 14: Cho parabol (P): y = x2 + x - 1 và đường thẳng (d): y = x + 2. Tọa độ giao điểm của (P) và (d) là:
A. (0;-1) B. (-2;0)
C. (1;-1) D. Kết quả khác
Đáp án
Cách 1:

Cách 2:
Thử trực tiếp từng cặp tọa độ (x;y) ở phương án A, B, C
Ta thấy không đồng thời thỏa mãn cả hai phương trình của (P) và (d).
Chọn đáp án D
Câu 15: Đồ thị hàm số y = |x2 - 4| cắt đường thẳng y = 2 tại:
A. một điểm
B. hai điểm
C. ba điểm
D. bốn điểm
Đáp án
Số giao điểm cần tìm bằng số nghiệm của phương trình: |x2 - 4| = 2
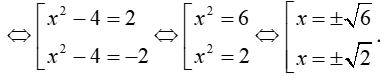
Ứng với 4 giá trị của x là 4 giao điểm của đồ thị và đường thẳng.
Chọn đáp án D
Câu 16: Parabol y = x2 + x + c cắt đường phân giác của góc phần tư thứ nhất tại điểm có hoành độ x = 1. Khi đó c bằng:
A. 1/2
B. -2
C. 2
D. -1
Đáp án
* Phương trình đường phân giác của góc phần tư thứ nhất là: y = x.
Với x = 1 thì y = 1.
Do đó, parabol cắt đường phân giác của góc phần tư thứ nhất tại A(1; 1).
Thay tọa độ A(1; 1) vào phương trình parabol ta được:
1 = 12 + 1 + c nên c = -1
Chọn đáp án D
Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 17: Dấu của tam thức bậc hai
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.