Toptailieu.vn xin giới thiệu 15 câu trắc nghiệm Biến cố và định nghĩa cổ điển của xác suất Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
15 câu trắc nghiệm Biến cố và định nghĩa cổ điển của xác suất Kết nối tri thức (có đáp án 2023) CHỌN LỌC
Lý thuyết
1. Biến cố
Ở lớp 9 ta đã biết những khái niệm quan trọng sau:
+ Phép thử ngấu nhiên (gọi tắt là phép thử) là một thí nghiệm hay một hành động mà kết quả của nó không thể biết được trước khi phép thử được thực hiện.
+ Không gian mẫu của phép thử là tập hợp tất cả các kết quả có thể khi thực hiện phép thử Không gian mẫu của phép thử được kí hiệu là Ω.
+ Kết quả thuận lợi cho một biến cố E liên quan tới phép thử T là kết quả của phép thử T làm cho biến cố đó xảy ra.
Chú ý: Ta chỉ xét các phép thử mà không gian mẫu gồm hữu hạn kết quả.
* Theo định nghĩa, ta thấy mỗi kết quả thuân lợi cho biến cố E chính là một phần tử thuộc không gian mẫu Ω. Do đó về mặt toán học, ta có:
Mỗi biến cố là một tập con của không gian mẫu. Tập con này là tập tất cae các kết quả thuận lợi cho biến cố đó.
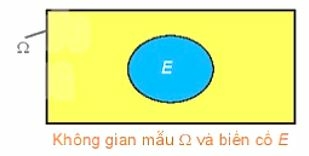
Nhận xét: Biến cố chắc chắn là tập Ω, biến cố không thể là tập Ø.
Biến cố đối của biến cố E là biến cố “E không xảy ra”. Biến cố đối của E được kí hiệu là .
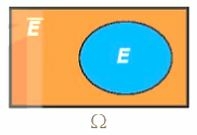
Nhận xét: Nếu biến cố E là tập con của không gian mẫu Ω thì biến cố đối ![]() là tập tất cả các phần tử của Ω mà không là phần tử của E. Vậy biến cố
là tập tất cả các phần tử của Ω mà không là phần tử của E. Vậy biến cố ![]() là phần bù của E trong
là phần bù của E trong ![]() .
.
2. Định nghĩa cổ điển của xác suất
Ta đã biết không gian mẫu Ω của phép thử T là tập hợp tất cả các kết quả có thể của T, biến có E liên quan đến phép thử T là tập con của Ω. Vì thế số kết quả có thể của phép thử T chính là số phần tử tập Ω; số kết quả thuận lợi của biến cố E chính là số phản tử của tập E. Do đó, ta có định nghĩa cổ điển của xác suất như sau:
Cho phép thử T có không gian mẫu là Ω. Giả thiết rằng các kết quả có thể của T là đồng khả năng. Khi đó nếu E là một biến cổ liên quan đến phép thử T thì xác suất của E được cho bởi công thức ![]() .
.
trong đỏ n(Ω) và n(E) tương ứng là số phần tử của tập Ω và tập E.
Nhận xét
+ Với mỗi biến cố E, ta có 0 ≤ P(E) ≤ 1.
+ Với biến cố chắc chắn (là tập Ω), ta có P(Ω) = 1.
+ Với biến cố không thể (là tập Ø), ta có P(Ø) = 0.
3. Nguyên lí xác suất bé
Qua thực tế người ta thấy rằng một biến cố có xác suất rất bé thì sẽ không xảy ra khi ta thực hiện một phép thử hay một vài phép thử. Từ đó người ta đã thừa nhận nguyên lí sau đây gọi là nguyên lí xác suất bé:
Nếu một biến có có xác suắt rất bé thì trong một phép thử biến cố đó sẽ không xảy ra.
Chẳng hạn, xác suất một chiếc máy bay rơi là rất bẻ, khoảng 0,00000027. Mỗi hành khách khi đi máy bay đều tin rằng biến cố: “Máy bay rơi” sẽ không xảy ra trong chuyến bay của mình, do đó người ta vẫn không ngân ngại đi máy bay.
Chú ý: Trong thực tế, xác suất của một biến cố được coi là bé phụ thuộc vào từng trường hợp cụ thể. Chẳng hạn, xác suất một chiếc điện thoại bị lối kĩ thuật là 0,001 được coi là rất bé, nhưng nếu xác suất cháy nỗ động cơ của một máy bay là 0,001 thỉ xác suất này không được coi là rất bé.
Bài tập
Câu 1. Gieo một đồng tiền liên tiếp 3 lần thì số phần tử của không gian mẫu n(Ω) là
A. 4;
B. 6;
C. 8;
D. 16.
Đáp án
Đáp án đúng là: C
Gieo đồng xu liên tiếp 3 lần nên ta có
Lần 1 có 2 khả năng xảy ra (có thể xuất hiện mặt sấp hoặc mặt ngửa).
Lần 2 có 2 khả năng xảy ra (có thể xuất hiện mặt sấp hoặc mặt ngửa).
Lần 3 có 2 khả năng xảy ra (có thể xuất hiện mặt sấp hoặc mặt ngửa).
Vậy số phần tử của không gian mẫu n(Ω) = 2.2.2 = 8.
Câu 2. Gieo một con xúc xắc cân đối đồng chất 2 lần. Số phần tử của không gian mẫu là?
A. 6;
B. 12;
C. 18;
D. 36.
Đáp án
Đáp án đúng là: D
Gieo một con xúc xắc cân đối đồng chất 2 lần nên ta có
Lần 1 có 6 khả năng sảy ra (số mặt xuất hiện từ 1 chấm đến 6 chấm).
Lần 2 có 6 khả năng sảy ra (số mặt xuất hiện từ 1 chấm đến 6 chấm).
Vậy số phần tử của không gian mẫu n(Ω) = 6.6 = 36.
Câu 3. Rút một lá bài từ bộ bài gồm 52 lá. Xác suất để được lá bích là
![]()
Đáp án
Đáp án đúng là: B
Số phần tử của không gian mẫu n(Ω) = 52 (vì chọn 1 lá bài trong 52 lá nên có 52 cách chọn)
Gọi A là biến cố lá bài rút được là bích.
Số phần tử của biến cố A là n(A) = 13 (vì một bộ bài có 13 lá bích, chọn 1 lá bích trong 13 lá bích có 13 cách chọn)
Vậy xác suất để lấy được lá bích là P(A) = ![]()
Câu 4. Gieo một đồng xu và một con xúc xắc cân đối đồng chất một lần. Số phần tử của không gian mẫu là:
A. 24
B. 12
C. 6
D. 8
Đáp án
Đáp án đúng là: B
Gieo đồng xu có 2 khả năng có thể sảy ra (hoặc là sấp hoặc là ngửa)
Gieo súc sắc có 6 khả năng có thể sảy ra ({1 chấm, 2 chấm, 3 chấm, 4 chấm, 5 chấm, 6 chấm}).
Số phần tử của không gian mẫu n(Ω) = 2.6 = 12.
Câu 5. Gieo đồng xu cân đối đồng chất hai lần. Số phần tử của biến cố để mặt ngửa xuất hiện đúng 1 lần là:
A. 2
B. 4
C. 5
D. 6
Đáp án
Đáp án đúng là: A
Vì mặt ngửa xuất hiện 1 lần nên chỉ có thể xuất hiện ở lần đầu gieo hoặc lần thứ 2 gieo nên số phần tử của biến cố là 2.
Do đó các kết quả thuận lợi cho biến cố A là: A = {NS; SN}.
Vậy có 2 kết quả thuận lợi cho A.
Câu 6. Một hộp đựng 10 thẻ, đánh số từ 1 đến 10. Chọn ngẫu nhiên 3 thẻ. Gọi A là biến cố để tổng số của 3 thẻ được chọn không vượt quá 8. Số phần tử của biến cố A là:
A. 2;
B. 3;
C. 4;
D. 5.
Đáp án
Đáp án đúng là: C
Vì các thẻ được đánh số từ 1 đến 10 chọn ngẫu nhiên 3 thẻ và tổng số 3 thẻ không vượt quá 8 nên ta có thể liệt kê số phần tử của biến cố A như sau:
A = {(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4)}.
Vậy số phần tử của biến cố A là 4.
Câu 7. Gieo hai con xúc xắc. Xác suất để tổng số chấm trên hai mặt chia hết cho 3 là:
![]()
Đáp án
Đáp án đúng là: C
Số phần tử không gian mẫu: n(Ω) = 6.6 = 36
Gọi A là biến cố tổng số chấm hai mặt chia hết cho 3.
Vì tổng số chấm hai mặt chia hết cho 3 nên ta liệt kê số phần tử của biến cố A như sau: A = {(1; 2); (1; 5); (2; 1); (2; 4); (3; 3); (3; 6); (4; 2); (4; 5); (5; 1); (5; 4); (6; 3); (6; 6)} có 12 cặp số thoả mãn nên số phần tử của biến cố A là n(A) = 12.
Suy ra P(A) =![]()
Câu 8. Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số từ S. Xác suất chọn được số lớn hơn 2500 là:
![]()
Đáp án
Đáp án đúng là: C
Số có 4 chữ số có dạng: ![]() (a ≠ 0)
(a ≠ 0)
Công đoạn 1, Chọn số a có 9 cách chọn (vì a có thể chọn ngẫu nhiên 1 trong 9 số từ 1 đến 9).
Công đoạn 2, chọn số b có 9 cách chọn (vì b ≠ a mà từ 0 đến 9 có 10 số nhưng b không được chọn lại số mà a đã chọn nên b còn 9 số để chọn).
Công đoạn 3, chọn số c có 8 cách chọn (vì c ≠ a, c ≠ b mà từ 0 đến 9 có 10 số nhưng c không được chọn lại số mà a và b đã chọn nên c còn 8 số để chọn).
Công đoạn 4, chọn số d có 7 cách chọn (vì d ≠ a, d ≠ b, d ≠ c mà từ 0 đến 9 có 10 số nhưng d không được chọn lại số mà a, b và c đã chọn nên d còn 7 số để chọn).
Số phần tử của không gian mẫu: n(S) = 9.9.8.7 = 4536.
Gọi A: “ tập hợp các số tự nhiên có 4 chữ số phân biệt và lớn hơn 2500” ta có các trường hợp sau:
Trường hợp 1, a > 2
Chọn a: có 7 cách chọn (vì a có thể chọn ngẫu nhiên 1 trong 7 số từ 3 đến 9).
Chọn b: có 9 cách chọn (vì b ≠ a mà từ 0 đến 9 có 10 số nhưng b không được chọn lại số mà a đã chọn nên b còn 9 số để chọn).
Chọn c: có 8 cách chọn (vì c ≠ a, c ≠ b mà từ 0 đến 9 có 10 số nhưng c không được chọn lại số mà a và b đã chọn nên c còn 8 số để chọn).
Chọn d: có 7 cách chọn (vì d ≠ a, d ≠ b, d ≠ c mà từ 0 đến 9 có 10 số nhưng d không được chọn lại số mà a, b và c đã chọn nên d còn 7 số để chọn).
Vậy trường hợp này có: 7.9.8.7 = 3528 (số).
Trường hợp 2, a = 2 và b > 5.
Chọn a: có 1 cách chọn (vì a = 2).
Chọn b: có 4 cách chọn (vì b có thể chọn 1 trong 4 số từ 6 đến 9).
Chọn c: có 8 cách chọn (vì c ≠ a, c ≠ b mà từ 0 đến 9 có 10 số nhưng c không được chọn lại số mà a và b đã chọn nên c còn 8 số để chọn).
Chọn d: có 7 cách chọn (vì d ≠ a, d ≠ b, d ≠ c mà từ 0 đến 9 có 10 số nhưng d không được chọn lại số mà a, b và c đã chọn nên d còn 7 số để chọn).
Vậy trường hợp này có: 1.4.8.7 = 224 (số).
Trường hợp 3, a = 2, b = 5 và c > 0
Chọn a: có 1 cách chọn (vì a = 2).
Chọn b: có 1 cách chọn (vì b = 5).
Chọn c: có 7 cách chọn (vì c ≠ a, c ≠ b mà c > 0 nên c có thể chọn một trong các số từ 1 đến 9 có 9 số nhưng c không được chọn lại số mà a và b đã chọn nên c còn 7 số để chọn).
Chọn d: có 7 cách chọn (vì d ≠ a, d ≠ b, d ≠ c mà từ 0 đến 9 có 10 số nhưng d không được chọn lại số mà a, b và c đã chọn nên d còn 7 số để chọn).
Vậy trường hợp này có: 1.1.7.7 = 49 (số).
Trường hợp 4, a = 2; b = 5; c = 0; d > 0
Chọn a: có 1 cách chọn (vì a = 2).
Chọn b: có 1 cách chọn (vì b = 5).
Chọn c: có 1 cách chọn (vì c = 0).
Chọn d: có 7 cách chọn (vì d ≠ a, d ≠ b, d ≠ c mà từ 0 đến 9 có 10 số nhưng d không được chọn lại số mà a, b và c đã chọn nên d còn 7 số để chọn).
Vậy trường hợp này có: 1.1.1.7 = 7 (số).
Như vậy số phần tử của biến cố A là n(A) = 3528 + 224 + 49 + 7 = 3808.
Suy ra xác suất của biến cố A là: P(A) = ![]()
Em nghĩ bài toán này nếu giải theo kiểu phần bù thì sẽ ngắn hơn nhiều ạ.
Câu 9. Có 2 học sinh nam và 6 học sinh nữ, xếp thành một hàng ngang một cách ngẫu nhiên. Xác định số phần tử của biến cố A “Hai học sinh nam luôn đứng cạnh nhau”
A. 8!
B. 120
C. 10080
D. 720
Đáp án
Đáp án đúng là: C
Vì 2 học sinh nam luôn đứng cạnh nhau nên ta coi 2 học sinh nam là một vị trí. Do đó xếp 2 học sinh nam và 6 học sinh nữ có 7! cách xếp và xếp 2 học sinh nam có 2! cách xếp.
Tổng kết ta có 2!.7! = 10080 cách xếp.
Vậy số phần tử của biến cố A là 10080.
Câu 10. Một người bỏ ngẫu nhiên ba lá thư vào ba chiếc phong bì đã ghi địa chỉ. Xác suất để có ít nhất một lá thư được bỏ đúng phong bì là:
![]()
Đáp án
Đáp án đúng là: B
Số phần tử không gian mẫu là: n(Ω) = 3! = 6 (vì xếp 3 lá thư vào 3 phòng bì)
Gọi A là biến cố “Có ít nhất một lá thư được bỏ đúng phong bì”.
Ta xét các trường hợp sau:
Trường hợp 1, nếu lá thứ nhất bỏ đúng phong bì, hai lá còn lại để sai thì có duy nhất 1 cách.
Trường hợp 2, nếu lá thứ hai bỏ đúng phong bì, hai lá còn lại để sai thì có duy nhất 1 cách
Trường hợp 3, nếu lá thứ ba bỏ đúng phong bì, hai lá còn lại để sai thì có duy nhất 1 cách.
Trường hợp 4, cả ba lá thư đều được bỏ đúng có duy nhất 1 cách.
Vậy số phần tử của biến cố A là n(A) = 4.
Vậy xác suất của biến cố A là: P(A) = ![]()
Câu 11. Một quân vua được đặt trên một ô giữa bàn cờ vua. Mỗi bước di chuyển, quân vua được chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng. Bạn An di chuyển quân vua ngẫu nhiên 3 bước. Tính xác suất sau 3 bước quân vua trở về ô xuất phát.

Đáp án
Đáp án đúng là: D
Tại mọi ô đang đứng, ông vua có 8 khả năng lựa chọn để bước sang ô bên cạnh.
Do đó không gian mẫu n(Ω) = 83 = 512.
Gọi A là biến cố “sau 3 bước quân vua trở về ô xuất phát”. Sau ba bước quân vua muốn quay lại ô ban đầu khi ông vua đi theo đường khép kín tam giác. Chia hai trường hợp:
Trường hợp 1, từ ô ban đầu đi đến ô đen, đến đây có 4 cách để đi bước hai rồi về lại vị trí ban đầu. Vậy trường hợp 1 có 4.4 = 16 cách
Trường hợp 2, từ ô ban đầu đi đến ô trắng, đến đây có 2 cách để đi bước hai rồi về lại vị trí ban đầu. Vậy trường hợp 2 có 4.2 = 8 cách
Do số phần tử của biến cố A là n(A) = 16 + 8 = 24.
Vậy xác suất của biến cố A là P(A) = ![]()
Câu 12. Gieo một đồng xu cân đối và đồng chất ba lần. Tính xác suất của biến cố A: “Kết quả của 3 lần gieo là như nhau”
![]()
Đáp án
Đáp án đúng là: D
Mỗi một lần gieo sẽ có 2 khả năng có thể xảy ra. Vậy số phần tử của không gian mẫu là: n(Ω) = 2.2.2 = 8
Gọi A là biến cố “kết quả 3 lần gieo là như nhau” ta liệt kê số phần tử của biến cố A như sau: A = {(S; S; S); (N; N; N)}.
Vậy số phần tử của biến cố A là: n(A) = 2.
Xác suất của biến cố A là: P(A) = ![]()
Câu 13. Từ các số tự nhiên 1, 2, 3, 4, 5, 6, 7, 8, 9 lấy ngẫu nhiên một số. Tính xác suất để lấy được số chia hết chia hết cho 3?
![]()
Đáp án
Đáp án đúng là: D
Số phần tử của không gian mẫu n(Ω) = 9 (vì lấy 1 số trong 9 số từ 1 đến 9)
Gọi A là biến cố “lấy được số chia hết cho 3”.
Vậy số phần tử của biến cố A là: n(A) = 3 (vì từ 1 đến 9 có 3 số chia hết cho 3 và lấy ra một số).
Xác suất của biến cố A là: P(A) = ![]()
Câu 14. Gieo một con súc sắc cân đối đồng chất 1 lần. Gọi A là biến cố “mặt có chấm lẻ xuất hiện”. Biến cố đối của biến cố A là
A. ![]() = {1; 3; 5}
= {1; 3; 5}
B. ![]() = {4; 5; 6}
= {4; 5; 6}
C. ![]() = {1; 2; 3}
= {1; 2; 3}
D. ![]() = {2; 4; 6}
= {2; 4; 6}
Đáp án
Đáp án đúng là: D
Số phần tử của không gian mẫu n(Ω) = {1; 2; 3; 4; 5; 6}
A là biến cố “mặt có chấm lẻ xuất hiện” số phần tử của biến cố A là: n(A) = {1; 3; 5}
Biến cố đối là “mặt có chấm chẵn xuất hiện” số phần tử của biến cố ![]() là: = {2; 4; 6}
là: = {2; 4; 6}
Câu 15. Gieo một con xúc sắc cân đối đồng chất 2 lần. Tính xác suất để tổng số chấm của hai lần gieo nhỏ hơn 6.
![]()
Đáp án
Đáp án đúng là: C
Số phần tử của không gian mẫu n(Ω) = 6.6 = 36 (vì mỗi lần gieo có 6 khả năng có thể sảy ra)
Gọi A là biến cố tổng số chấm của hai lần gieo nhỏ hơn 6. Ta liệt kê các phần tử của biến cố A như sau: A = {(1; 1); (1; 2); (1; 3); (1; 4); (2; 1); (2; 2); (2; 3); (3; 1); (3; 2); (4; 1)}.
Vậy số phần tử của biến cố A là: n(A) = 10
Xác suất của biến cố A là: P(A) = ![]()
Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.