Với giải Bài 9.23 trang 56 SBT Toán 8 Tập 2 Kết nối tri thức chi tiết trong Bài 34: Ba trường hợp đồng dạng của hai tam giác dạng giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Cho tam giác ABC và hai điểm M, N lần lượt nằm trên hai cạnh AB, AC sao cho MN song song với BC
Bài 9.23 trang 56 SBT Toán lớp 8 Tập 2: Cho tam giác ABC và hai điểm M, N lần lượt nằm trên hai cạnh AB, AC sao cho MN song song với BC. Gọi ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và tam giác ABC. Chứng minh rằng:
a) ∆MEN ᔕ ∆BFC.
b) .
Lời giải:
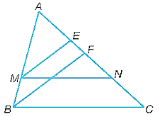
a)
Vì MN song song với BC (gt) nên
(hai góc đồng vị);
(hai góc đồng vị).
Mà ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và tam giác ABC nên và . Do đó, .
Tam giác MEN và tam giác BFC có:
(cmt)
(cmt)
Do đó, tam giác MEN đồng dạng với tam giác BFC (g.g).
b)
Tam giác ABC có:
MN song song với BC
Nên theo hệ quả định lý Thalès ta có:
(1).
Vì ME, BF lần lượt là phân giác của , của tam giác AMN và tam giác ABC nên .
Do đó , mà hai góc này ở vị trí đồng vị nên ME song song với BF.
Tam giác ABF có ME song song với BF nên theo hệ quả định lý Thalès ta có:
(2).
Từ (1) và (2) ta có: .
Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác:
Bài 9.12 trang 55 SBT Toán lớp 8 Tập 2: Hai tam giác có độ dài ba cạnh như sau có đồng dạng không ? Vì sao ?
Bài 9.13 trang 55 SBT Toán lớp 8 Tập 2: Cho hai tam giác ABC và DEF lần lượt có chu vi là 15 cm và 20 cm.
Bài 9.14 trang 55 SBT Toán lớp 8 Tập 2: Cho hai tam giác ABC và MNP thỏa mãn 2AB = 3AC = 4BC và DE = 6 cm, DF = 4 cm, EF = 4 cm.
Bài 9.15 trang 55 SBT Toán lớp 8 Tập 2: Cho tam giác ABC và điểm O nằm trong tam giác. Lấy M, N, P là các điểm lần lượt trên các tia OA, OB, OC sao cho OA = 3OM, OB = 3ON, OC = 3OP.
Bài 9.16 trang 55 SBT Toán lớp 8 Tập 2: Cho tam giác ABC và các điểm M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB.
Bài 9.17 trang 55 SBT Toán lớp 8 Tập 2: Cho tứ giác ABCD với AB = 2 cm, AD = 3 cm, BD = 4 cm, BC = 6 cm, CD = 8 cm.
Bài 9.18 trang 55 SBT Toán lớp 8 Tập 2: Cho tam giác ABC có độ dài các cạnh là AB = 4 cm, BC = 5 cm, CA = 6 cm.
Bài 9.19 trang 55 SBT Toán lớp 8 Tập 2: Với hai tam giác ABC và DEF bất kì thỏa mãn , .
Bài 9.20 trang 56 SBT Toán lớp 8 Tập 2: Với hai tam giác bất kì ABC và MNP thỏa mãn , .
Bài 9.21 trang 56 SBT Toán lớp 8 Tập 2: Cho hai điểm M, N lần lượt nằm trên hai cạnh AB, AC của tam giác ABC sao cho AM . AB = AN . AC.
Bài 9.22 trang 56 SBT Toán lớp 8 Tập 2: Cho tam giác ABC và hai điểm P, Q lần lượt nằm trên các tia đối của tia AB và AC sao cho .
Bài 9.23 trang 56 SBT Toán lớp 8 Tập 2: Cho tam giác ABC và hai điểm M, N lần lượt nằm trên hai cạnh AB, AC sao cho MN song song với BC.
Bài 9.24 trang 56 SBT Toán lớp 8 Tập 2: Cho hình thang ABCD (AB // CD). Biết rằng AB = 2 cm, BD = 4 cm, CD = 8 cm. Chứng minh rằng BC = 2AD
Bài 9.25 trang 56 SBT Toán lớp 8 Tập 2: Cho hình thang ABCD (AB // CD). Biết rằng AD cắt BC tại E, AC cắt BD tại F.
Bài 9.26 trang 56 SBT Toán lớp 8 Tập 2: Cho tam giác ABC với AB = 6 cm, AC = 9 cm. Lấy điểm D trên cạnh AC sao cho AD = 4 cm.
Bài 9.27 trang 57 SBT Toán lớp 8 Tập 2: Cho tứ giác ABCD như Hình 9.6. Biết rằng AB = 2 cm, AC = 4 cm, AD = 8 cm và AC là phân giác của góc BAD.
Bài 9.28 trang 57 SBT Toán lớp 8 Tập 2: Cho tam giác ABC và điểm D trên cạnh AC sao cho . Chứng minh rằng: AB2 = AD . AC.
Bài 9.29 trang 57 SBT Toán lớp 8 Tập 2: Cho hai điểm M, N lần lượt nằm trên các cạnh AB, AC của tam giác ABC sao cho . Gọi O là giao điểm của BN và CM.
Bài 9.30 trang 57 SBT Toán lớp 8 Tập 2: Cho tam giác ABC với AB = 6 cm, AC = 4 cm, BC = 5 cm. Trên tia đối của tia CA lấy điểm D sao cho CD = CB.
Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác:
Bài 33: Hai tam giác đồng dạng
Bài 35: Định lí Pythagore và ứng dụng
Bài 36: Các trường hợp đồng dạng của hai tam giác vuông
Bài 37: Hình đồng dạng
Bài tập cuối chương 9
