Với giải Luyện tập 2 trang 64 Toán 8 Tập 2 Cánh Diều chi tiết trong Bài 3: Đường trung bình của tam giác giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Luyện tập 2 trang 64 Toán 8 Tập 2 | Cánh Diều Giải Toán lớp 8
Luyện tập 2 trang 64 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD). Giả sử M, N, P lần lượt là trung điểm của các đoạn thẳng AD, BC, AC. Chứng minh:
a) M, N, P thẳng hàng;
b)
Lời giải:
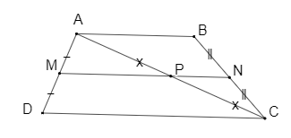
a) Vì M và P lần lượt là trung điểm của hai cạnh AD, AC nên MP là đường trung bình của tam giác ADC.
Suy ra MP // CD.
Mà AB // CD nên MP // AB // CD (1)
Tương tự, ta cũng có PN là đường trung bình của tam giác ABC.
Suy ra PN // AB // CD (2)
Từ (1) và (2), theo tiên đề Euclid, ta có MPvàPN trùng nhau hay ba điểm M, N, P thẳng hàng.
b) Vì MP là đường trung bình của tam giác ADC nên
Vì PN là đường trung bình của tam giác ABC nên
Ta có:
Vậy
Bài tập
Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác:
Khởi động trang 62 Toán 8 Tập 2: Hình 28 gợi nên hình ảnh tam giác ABC và đoạn thẳng MN với M, N lần lượt là trung điểm của hai cạnh AB, AC.
Hoạt động 1 trang 62 Toán 8 Tập 2: Quan sát tam giác ABC ở Hình 29 và cho biết hai đầu mút D, E của đoạn thẳng DE có đặc điểm gì.
Luyện tập 1 trang 62 Toán 8 Tập 2: Vẽ tam giác ABC và các đường trung bình của tam giác đó.
Hoạt động 2 trang 63 Toán 8 Tập 2: Cho tam giác ABC có MN là đường trung bình (Hình 31).
Luyện tập 2 trang 64 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD). Giả sử M, N, P lần lượt là trung điểm của các đoạn thẳng AD, BC, AC. Chứng minh:
Bài 1 trang 65 Toán 8 Tập 2:Cho tam giác ABC có M là trung điểm của AB, điểm N thuộc cạnh AC thoả mãn MN // BC. Chứng minh NA = NC và
Bài 2 trang 65 Toán 8 Tập 2: Cho tam giác ABC có AM là đường trung tuyến, các điểm N, P phân biệt thuộc cạnh AB sao cho AP = PN = NB. Gọi Q là giao điểm của AM và CP. Chứng minh:
Bài 3 trang 65 Toán 8 Tập 2: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
Bài 4 trang 65 Toán 8 Tập 2: Cho tam giác ABC nhọn có H là trực tâm. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AB, BH, HC, CA. Chứng minh tứ giác MNPQ là hình chữ nhật.
Bài 5 trang 65 Toán 8 Tập 2: Trong Hình 36, ba cạnh màu vàng AB, BC, CA gợi nên hình ảnh tam giác ABC ...
Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác:
Bài 2: Ứng dụng của định lí Thalès trong tam giác
Bài 4: Tính chất đường phân giác của tam giác
Bài 5: Tam giác đồng dạng
Bài 6: Trường hợp đồng dạng thứ nhất của tam giác
Bài 7: Trường hợp đồng dạng thứ hai của tam giác