Bài 1.40 trang 43 Toán 12 Tập 1 | Kết nối tri thức Giải Toán lớp 12

Mai Hương Ngày: 14-03-2024 Lớp 12

191

Với giải Bài 1.40 trang 43 Toán 12 Tập 1 Kết nối tri thức chi tiết trong Bài tập cuối chương 1 trang 42 giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Bài 1.40 trang 43 Toán 12 Tập 1 | Kết nối tri thức Giải Toán lớp 12

Bài 1.40 trang 43 SGK Toán 12 Tập 1: Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau:

a) $y = x^{3} - 3 x^{2} + 3 x - 1$ ;
b) $y = x^{4} - 2 x^{2} - 1$ ;
c) $y = \frac{2 x - 1}{3 x + 1}$ ;
d) $y = \frac{x^{2} + 2 x + 2}{x + 1}$ .

Lời giải:

a) Tập xác định: $D = R$ .

Ta có: $y^{'} = 3 x^{2} - 6 x + 3 = 3 {(x - 1)}^{2}, y^{'} = 0 \Leftrightarrow x = 1$

Lập bảng biến thiên của hàm số:

Hàm số $y = x^{3} - 3 x^{2} + 3 x - 1$ đồng biến trên khoảng $(- \infty; 1)$ và $(1; + \infty)$ .

Hàm số $y = x^{3} - 3 x^{2} + 3 x - 1$ không có cực trị.

b) Tập xác định của hàm số là $D = R$ .

Ta có: $y^{'} = 4 x^{3} - 4 x, y^{'} = 0 \Leftrightarrow 4 x^{3} - 4 x = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = \pm 1 \end{array}$

Bảng biến thiên:

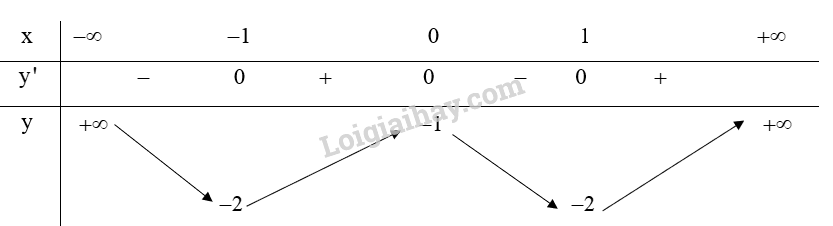
Từ bảng biến thiên ta có:

Hàm số $y = x^{4} - 2 x^{2} - 1$ đồng biến trên khoảng $(- 1; 0)$ và $(1; + \infty)$ .

Hàm số $y = x^{4} - 2 x^{2} - 1$ nghịch biến trên khoảng $(- \infty; - 1)$ và $(0; 1)$ .

Hàm số $y = x^{4} - 2 x^{2} - 1$ đạt cực đại tại $x = 0$ và .

Hàm số $y = x^{4} - 2 x^{2} - 1$ đạt cực tiểu tại $x = \pm 1$ và $y_{C T} = - 2$ .

c) Tập xác định: $D = R ∖ {- \frac{1}{3}}$ .

Ta có: $y^{'} = \frac{2 (3 x + 1) - 3 (2 x - 1)}{{(3 x + 1)}^{2}} = \frac{5}{{(3 x + 1)}^{2}} > 0 \forall x \neq \frac{- 1}{3}$

Lập bảng biến thiên của hàm số:

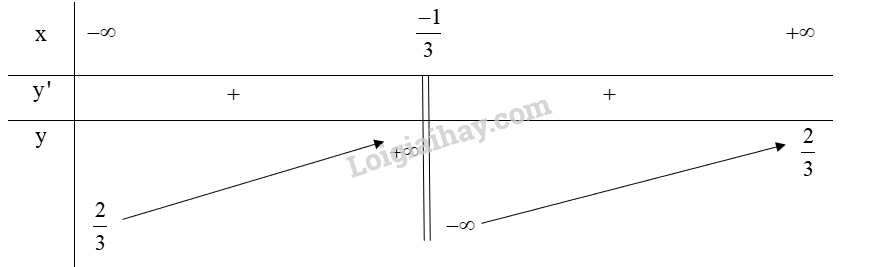
Từ bảng biến thiên ta có:

Hàm số $y = \frac{2 x - 1}{3 x + 1}$ đồng biến trên $(- \infty; \frac{- 1}{3})$ và $(\frac{- 1}{3}; + \infty)$ .

Hàm số không có cực trị.

d) Tập xác định: $D = R ∖ {- 1}$ .

Ta có: $y^{'} = \frac{(2 x + 2) (x + 1) - (x^{2} + 2 x + 2)}{{(x + 1)}^{2}} = \frac{x^{2} + 2 x}{{(x + 1)}^{2}}$

$y^{'} = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = - 2 \end{array}$ (thỏa mãn)

Lập bảng biến thiên của hàm số:

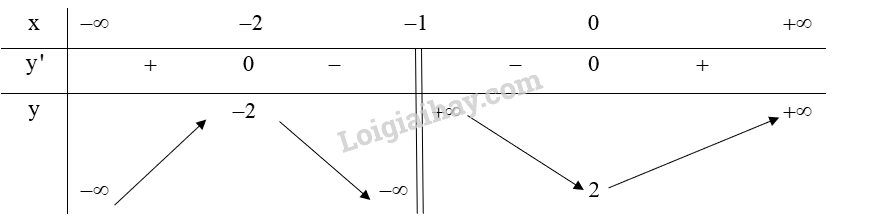
Từ bảng biến thiên ta có:

Hàm số $y = \frac{x^{2} + 2 x + 2}{x + 1}$ đồng biến trên khoảng $(- \infty; - 2)$ và $(0; + \infty)$ .

Hàm số $y = \frac{x^{2} + 2 x + 2}{x + 1}$ nghịch biến trên khoảng $(- 2; - 1)$ và $(- 1; 0)$ .

Hàm số $y = \frac{x^{2} + 2 x + 2}{x + 1}$ đạt cực đại tại $x = - 2$ và .

Hàm số $y = \frac{x^{2} + 2 x + 2}{x + 1}$ đạt cực tiểu tại $x = 0$ và $y_{C T} = 2$ .

Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Bài 1.30 trang 42 SGK Toán 12 Tập 1: Cho hàm số $y = f (x)$ có đạo hàm trên khoảng (a; b). Phát biểu nào dưới đây là đúng?

Bài 1.31 trang 42 SGK Toán 12 Tập 1: Hàm số nào sau đây nghịch biến trên $R$ ?

Bài 1.32 trang 42 SGK Toán 12 Tập 1: Hàm số nào dưới đây không có cực trị?

Bài 1.33 trang 42 SGK Toán 12 Tập 1: Giá trị cực tiểu của hàm số $y = x^{2} \ln x$ là

Bài 1.34 trang 42 SGK Toán 12 Tập 1: Giá trị lớn nhất của hàm số

y = {(x - 2)}^{2} . e^{x}

trên đoạn [1; 3] là:

Bài 1.35 trang 42 SGK Toán 12 Tập 1: Cho hàm số

y = f (x)

thỏa mãn:

lim_{x \to 2^{+}} f (x) = 1; lim_{x \to 2^{-}} f (x) = 1; lim_{x \to - \infty} f (x) = 2

và

lim_{x \to + \infty} f (x) = 2

. Khẳng định nào sau đây là đúng?

Bài 1.36 trang 42 SGK Toán 12 Tập 1: Tiệm cận xiên của đồ thị hàm số $y = \frac{x^{2} + 2 x - 2}{x + 2}$ là

Bài 1.37 trang 43 SGK Toán 12 Tập 1: Cho hàm số $y = f (x)$ xác định trên $R ∖ {1; 3}$ , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

Bài 1.38 trang 43 SGK Toán 12 Tập 1: Đồ thị trong Hình 1.37 là đồ thị của hàm số:

Bài 1.39 trang 43 SGK Toán 12 Tập 1: Đồ thị trong Hình 1.38 là đồ thị của hàm số:

Bài 1.38 trang 43 SGK Toán 12 Tập 1: Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau:

Bài 1.39 trang 43 SGK Toán 12 Tập 1: Đồ thị trong Hình 1.38 là đồ thị của hàm số:

Bài 1.40 trang 43 SGK Toán 12 Tập 1: Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau: a) $y = x^{3} - 3 x^{2} + 3 x - 1$ ;

Bài 1.41 trang 44 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a)

y = \frac{2 x + 1}{3 x - 2}

trên nửa khoảng

[2; + \infty)

;

Bài 1.42 trang 44 SGK Toán 12 Tập 1: Tìm các tiệm cận của mỗi đồ thị hàm số sau: a) $y = \frac{3 x - 2}{x + 1}$ ;

Bài 1.43 trang 44 SGK Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) $y = - x^{3} + 6 x^{2} - 9 x + 12$ ;

Bài 1.44 trang 44 SGK Toán 12 Tập 1: Xét một thấu kính hội tụ có tiêu cự f (H.1.39). Khoảng cách p từ vật đến thấu kính liên hệ với khoảng cách q từ ảnh đến thấu kính bởi hệ thức:

\frac{1}{p} + \frac{1}{q} = \frac{1}{f}

Bài 1.45 trang 44 SGK Toán 12 Tập 1: Dân số của một quốc gia sau t (năm) kể từ năm 2023 được ước tính bởi công thức:

N (t) = 100 e^{0, 012 t}

(N(t) được tính bằng triệu người,

0 \leq t \leq 50

Bài 1.46 trang 44 SGK Toán 12 Tập 1: Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như Hình 1.40. Khoảng cách từ C đến B là 4km.

Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Từ khóa :

Giải bài tập Toán 12

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

205

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

243

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

263

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

219