Với giải Câu hỏi trang 7 Toán 10 Tập 2 Chân trời sáng tạo trong Bài 1: Dấu của tam thức bậc hai giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Chân trời sáng tạo trang 10 Bài 1: Dấu của tam thức bậc hai
Phương pháp giải
Bước 1: Xác định nghiệm của tam thức (là giao điểm của đồ thị với trục hoành)
Bước 2: Xác định khoảng mà (khoảng đồ thị nằm trên trục hoành)
Bước 3: Xác định khoảng mà (khoảng đồ thị nằm dưới trục hoành)
Bước 4: Lập bảng xét dấu
Lời giải
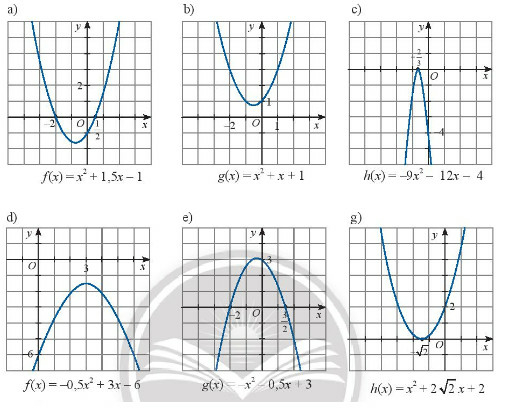
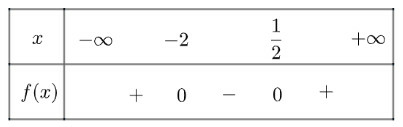
a) Tam thức có hai nghiệm phân biệt
khi và khi
Ta có bảng xét dấu như sau
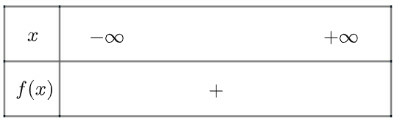
b) Tam thức vô nghiệm,
Ta có bảng xét dấu như sau
c) Tam thức có nghiệm kép và
Ta có bảng xét dấu như sau
d) Tam thức vô nghiệm và
Ta có bảng xét dấu như sau:

e) Tam thức có hai nghiệm
khi và khi
Ta có bảng xét dấu như
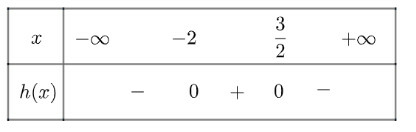
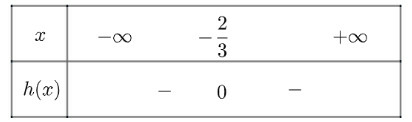
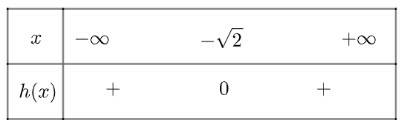
g) Tam thức có nghiệm kép
Ta có bảng xét dấu như sau
Bài 4 trang 10 Toán 10 Tập 2: Xét dấu của các tam thức bậc hai sau đây:
a)
b)
c)
d)
e)
Phương pháp giải
Bước 1: Tính và xác định dấu của biệt thức
Bước 2: Xác định nghiệm của (nếu có)
Bước 3: Xác định dấu của hệ số
Bước 4: Xác định dấu của
Lời giải
a) có , có nghiệm kép là
và
Ta có bảng xét dấu như sau:
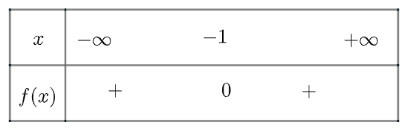
Vậy dương với mọi
b) có , hai nghiệm phân biệt là
và
Ta có bảng xét dấu như sau:
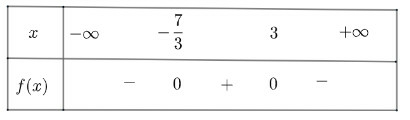
Vậy dương với và âm khi
c) có , tam thức vô nghiệm
và
Ta có bảng xét dấu như sau:

Vậy âm với mọi
d) có , tam thức có nghiệm kép và
Ta có bảng xét dấu như sau
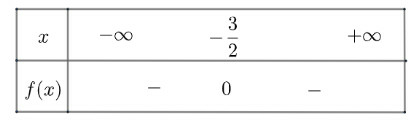
Vậy âm với mọi
e) có , có hai nghiệm phân biệt và có
Ta có bảng xét dấu như sau
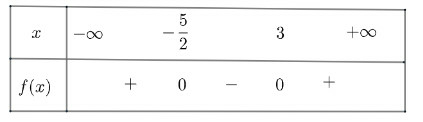
Vậy âm với và dương khi
Phương pháp giải
Bước 1: Tính và xác định dấu của biệt thức
Bước 2: Xác định nghiệm của (nếu có)
Bước 3: Lập bảng xét dấu
Bước 4: Dựa vào bảng xét dấu đưa ra các khoảng theo yêu cầu
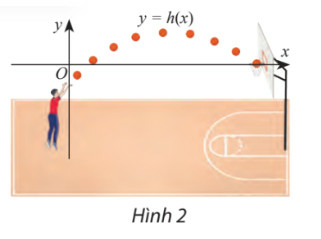
+) Khoảng mà là khoảng bóng nằm cao hơn vành rổ
+) Khoảng mà là khoảng bóng nằm thấp hơn vành rổ
+) Khoảng mà là khoảng bóng nằm ngang vành rổ
Lời giải
có , có hai nghiệm phân biệt là
Ta có bảng xét dấu như sau:

Vậy khoảng bóng nằm trên vành rổ là mét
khoảng bóng nằm dưới vành rổ là mét
khoảng bóng nằm ngang vành rổ là
Phương pháp giải
Bước 1: Lập hiệu giữa diện tích mới và diện tích cũ với
Bước 2: Tìm các khoảng thỏa mãn yêu cầu
+) Khoảng mà là khoảng diện tích tăng lên
+) Khoảng mà là khoảng diện tích giảm đi
+) Khoảng mà là khoảng diện tích không đổi
Lời giải
Theo giải thiết ta có tam thức sau:
Tam thức có , có hai nghiệm phân biệt
Ta có bảng xét dấu như sau
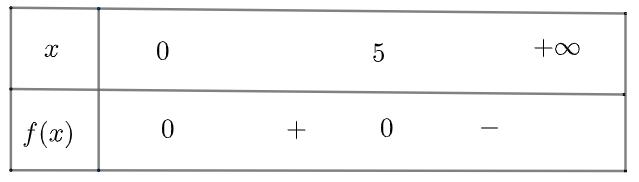
Vậy khoảng diện tích tăng lên là , khoảng diện giảm đi là và diện tích không đổi khi và
Chú ý khi giải:
Vì x là độ dài nên điều kiện hiển nhiên của x là .
Bài 7 trang 10 Toán 10 Tập 2: Chứng minh rằng với mọi số thực m ta luôn có
Phương pháp giải
Bước 1: Chuyển bất phương trình tương đương với
Bước 2: Tính và chỉ ra dấu của âm
Bước 3: Áp dụng tính chất của tam thức bậc hai
Lời giải
Yêu cầu bài toán tương đương chứng minh với mọi m
Tam thức có
Áp dụng định lí về dấu của tam thức bậc hai ta có
và nên cùng dấu với a với mọi m
Vậy với mọi m với mọi m.
Bài 8 trang 10 Toán 10 Tập 2: Tìm giá trị của m để:
a) với mọi ;
b) với mọi
Phương pháp giải
a) Bước 1: Tính và xác định dấu của a
Bước 2: với mọi khi và
b) Bước 1: Tính và xác định dấu của a
Bước 2: với mọi khi và
Lời giải
a) Tam thức có
Vì nên để với mọi khi và chỉ khi
Vậy khi thì với mọi
b) Tam thức có
Đề với mọi khi và chỉ khi và
Vậy với mọi khi .
Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:
HĐ Khám phá 1 trang 6 Toán 10 Tập 2: Đồ thị của hàm số được biểu diễn trong hình 1
Thực hành 2 trang 7 Toán 10 Tập 2: Tìm biệt thức và nghiệm của các tam thức bậc hai sau...
Thực hành 3 trang 9 Toán 10 Tập 2: Xét dấu của các tam thức bậc hai sau...
Bài 1 trang 9 Toán 10 Tập 2: Đa thức nào sau đây là tam thức bậc hai?...
Bài 2 trang 9 Toán 10 Tập 2: Xác định giá trị của m để các đa thức sau là tam thức bậc hai...
Bài 4 trang 10 Toán 10 Tập 2: Xét dấu của các tam thức bậc hai sau đây...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.